Термин обратное нормальное распределение относится к методу использования известной вероятности для нахождения соответствующего z-критического значения в нормальном распределении .
Это не следует путать с обратным распределением Гаусса , которое является непрерывным распределением вероятностей.
В этом руководстве представлено несколько примеров использования обратного нормального распределения в различных статистических программах.
Обратное нормальное распределение на калькуляторе TI-83 или TI-84
Скорее всего, вы встретите термин «обратное нормальное распределение» на калькуляторе TI-83 или TI-84, который использует следующую функцию для нахождения критического значения z, соответствующего определенной вероятности:
invNorm(вероятность, μ, σ)
куда:
- вероятность: уровень значимости
- μ: среднее значение населения
- σ: стандартное отклонение населения
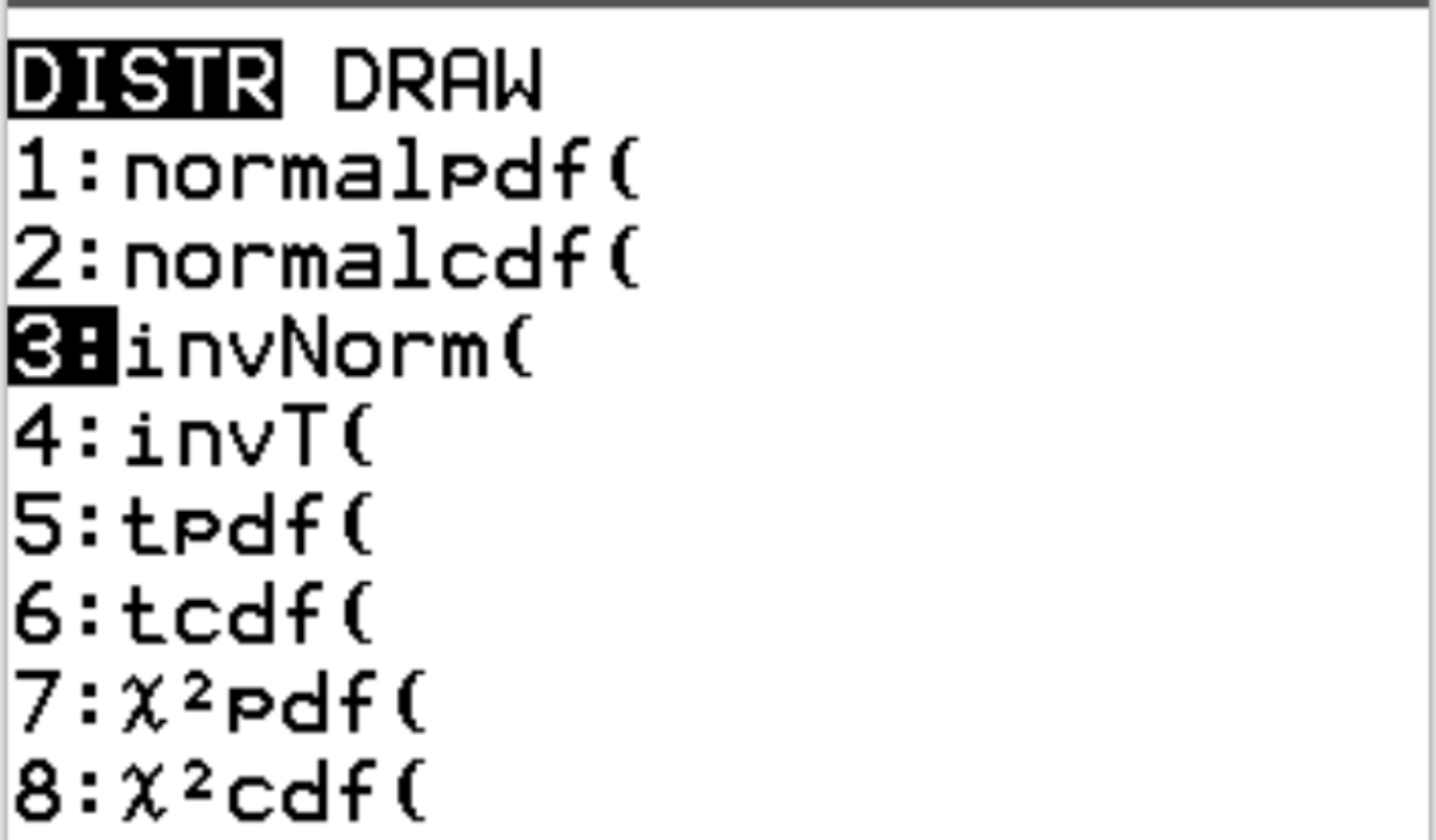
Вы можете получить доступ к этой функции на калькуляторе TI-84, нажав 2nd , а затем нажав vars.Это приведет вас к экрану DISTR , где вы сможете использовать invNorm() :
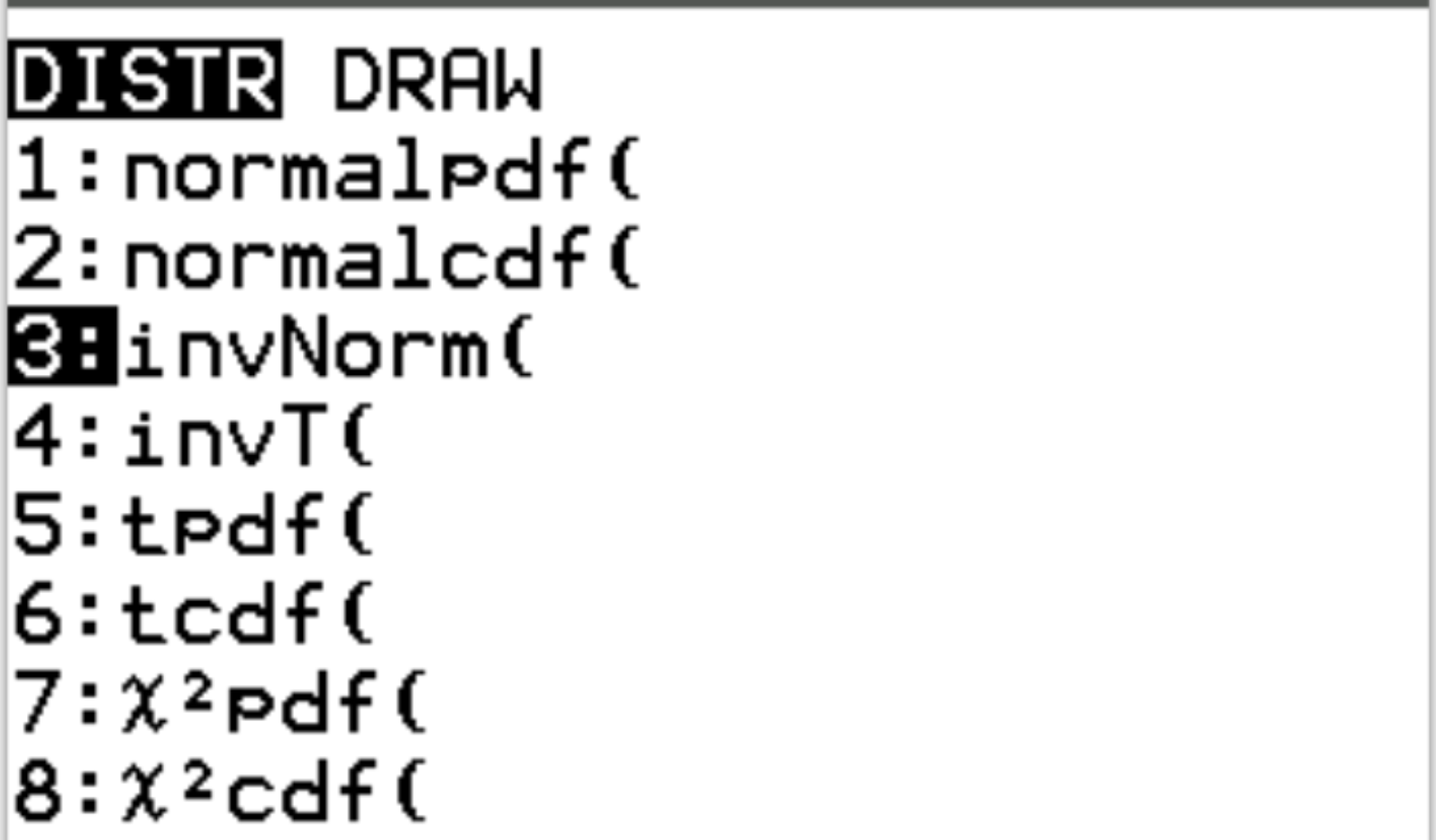
Например, мы можем использовать эту функцию, чтобы найти z-критическое значение, соответствующее значению вероятности 0,05:
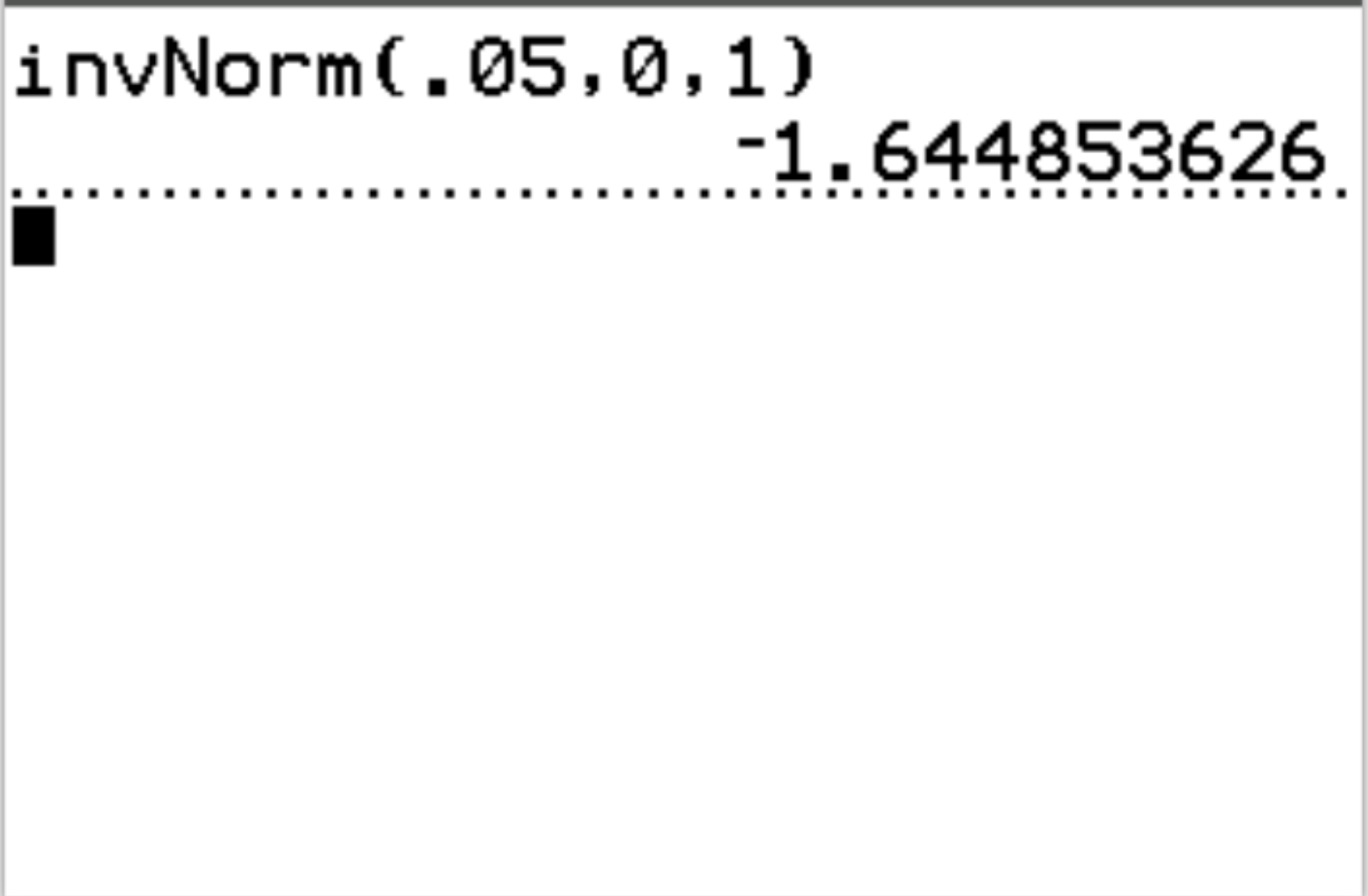
Z-критическое значение, соответствующее значению вероятности 0,05, равно -1,64485 .
Связанный: Как использовать invNorm на калькуляторе TI-84 (с примерами)
Обратное нормальное распределение в Excel
Чтобы найти z-критическое значение, связанное с определенным значением вероятности в Excel, мы можем использовать функцию ПРОБРНОРМ() , которая использует следующий синтаксис:
INVNORM(p, среднее, sd)
куда:
- p: уровень значимости
- среднее значение: среднее значение населения
- sd: стандартное отклонение населения
Например, мы можем использовать эту функцию, чтобы найти z-критическое значение, соответствующее значению вероятности 0,05:

Z-критическое значение, соответствующее значению вероятности 0,05, равно -1,64485 .
Обратное нормальное распределение в R
Чтобы найти z-критическое значение, связанное с определенным значением вероятности в R, мы можем использовать функцию qnorm() , которая использует следующий синтаксис:
qnorm(p, среднее, sd)
куда:
- p: уровень значимости
- среднее значение: среднее значение населения
- sd: стандартное отклонение населения
Например, мы можем использовать эту функцию, чтобы найти z-критическое значение, соответствующее значению вероятности 0,05:
qnorm (p= .05 , mean= 0 , sd= 1 )
[1] -1.644854
И снова критическое значение z, соответствующее значению вероятности 0,05, равно -1,64485 .