Вы можете использовать функцию invNorm() на калькуляторе TI-84, чтобы найти критические значения z, связанные с нормальным распределением .
Эта функция использует следующий синтаксис:
invNorm(вероятность, μ, σ)
куда:
- вероятность: уровень значимости
- μ: среднее значение населения
- σ: стандартное отклонение населения
Вы можете получить доступ к этой функции на калькуляторе TI-84, нажав 2 -ю, а затем нажав VARS.Это приведет вас к экрану DISTR , где вы сможете использовать invNorm() :
В следующих примерах показано, как использовать эту функцию на практике.
Пример 1: Z-критическое значение для односторонних тестов
Предположим, исследователь проводит проверку левосторонней гипотезы, используя α = 0,05. Какое z-критическое значение соответствует этому альфа-уровню?
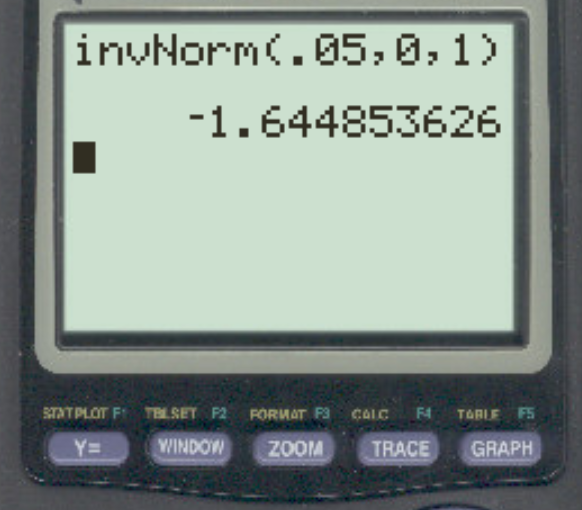
Ответ: z = -1,64485 .
Предположим, исследователь проводит проверку правосторонней гипотезы, используя α = 0,05. Какое z-критическое значение соответствует этому альфа-уровню?
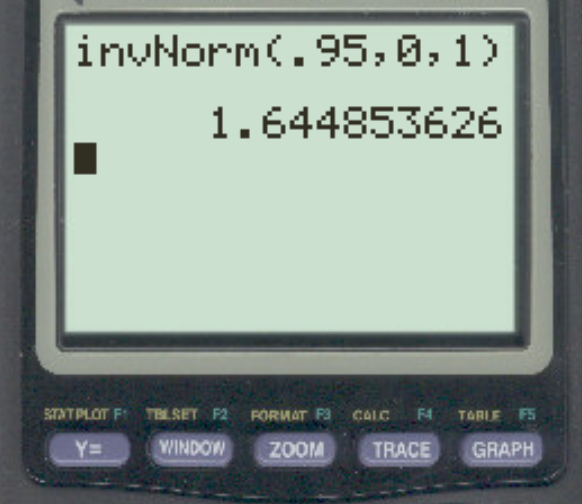
Ответ: z = 1,64485 .
Пример 2: Z-критическое значение для двусторонних тестов
Предположим, исследователь проводит двустороннюю проверку гипотезы, используя α = 0,05. Какое z-критическое значение соответствует этому альфа-уровню?
Чтобы найти это критическое значение, мы можем использовать формулу 1 – α/2. В этом случае мы будем использовать 1 – 0,05/2 = 0,975 для вероятности:
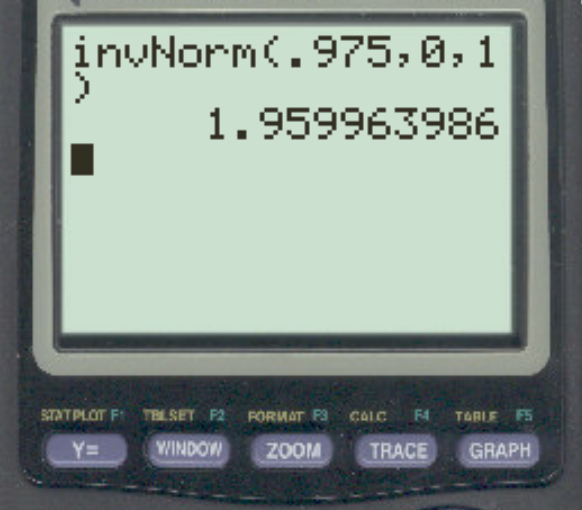
Ответ: z = 1,96 .
Пример 3: Z-критическое значение для пороговых значений
Предположим, баллы за конкретный экзамен нормально распределены со средним значением 70 и стандартным отклонением 8. Какой балл отделяет 10% лучших от остальных?
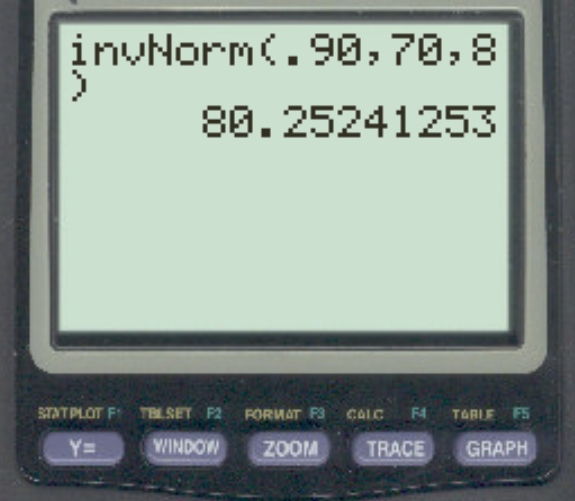
Ответ 80,25 .
Предположим, рост мужчин в определенном городе распределен нормально со средним значением 68 дюймов и стандартным отклонением 4 дюйма. Какая высота отделяет нижние 25% от остальных?
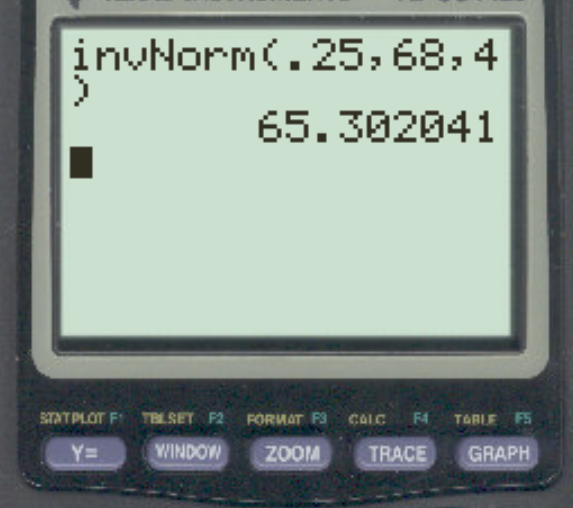
Ответ: 65,3 дюйма.
Дополнительные ресурсы
Как рассчитать биномиальные вероятности на калькуляторе TI-84
Как рассчитать вероятности Пуассона на калькуляторе TI-84
Как рассчитать геометрические вероятности на калькуляторе TI-84