Распределение Пуассона является одним из наиболее часто используемых распределений во всей статистике. В этом руководстве объясняется, как использовать следующие функции калькулятора TI-84 для нахождения вероятности Пуассона:
poissonpdf(mean, x) возвращает вероятность, связанную с PDF Пуассона.
poissoncdf(mean, x) возвращает кумулятивную вероятность, связанную с cdf Пуассона.
куда:
- среднее = среднее количество «успехов»
- x = конкретное количество «успехов»
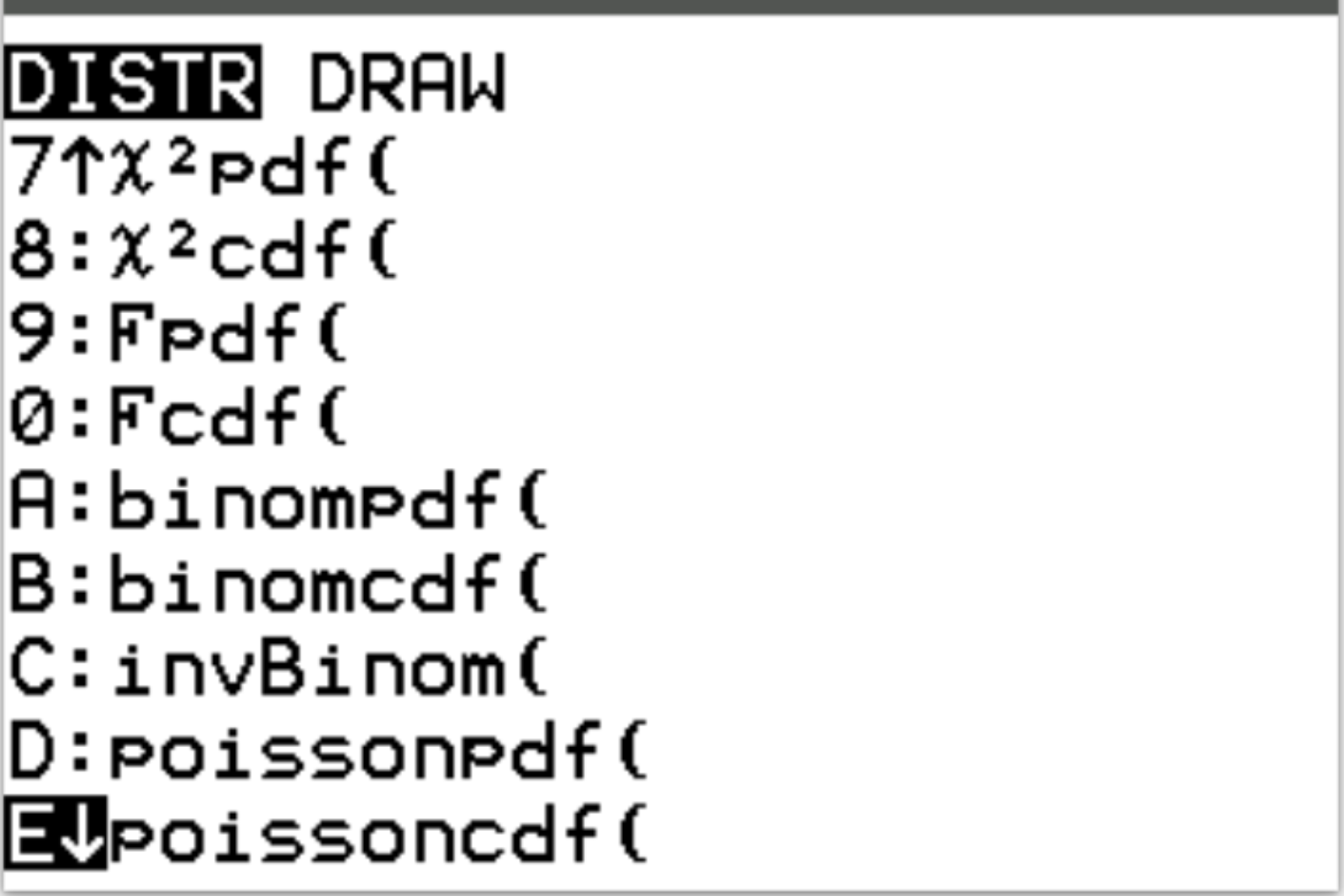
Доступ к обеим этим функциям можно получить на калькуляторе TI-84, нажав 2nd , а затем нажав vars.Это приведет вас к экрану DISTR , где вы сможете использовать poissonpdf() и poissoncdf() :
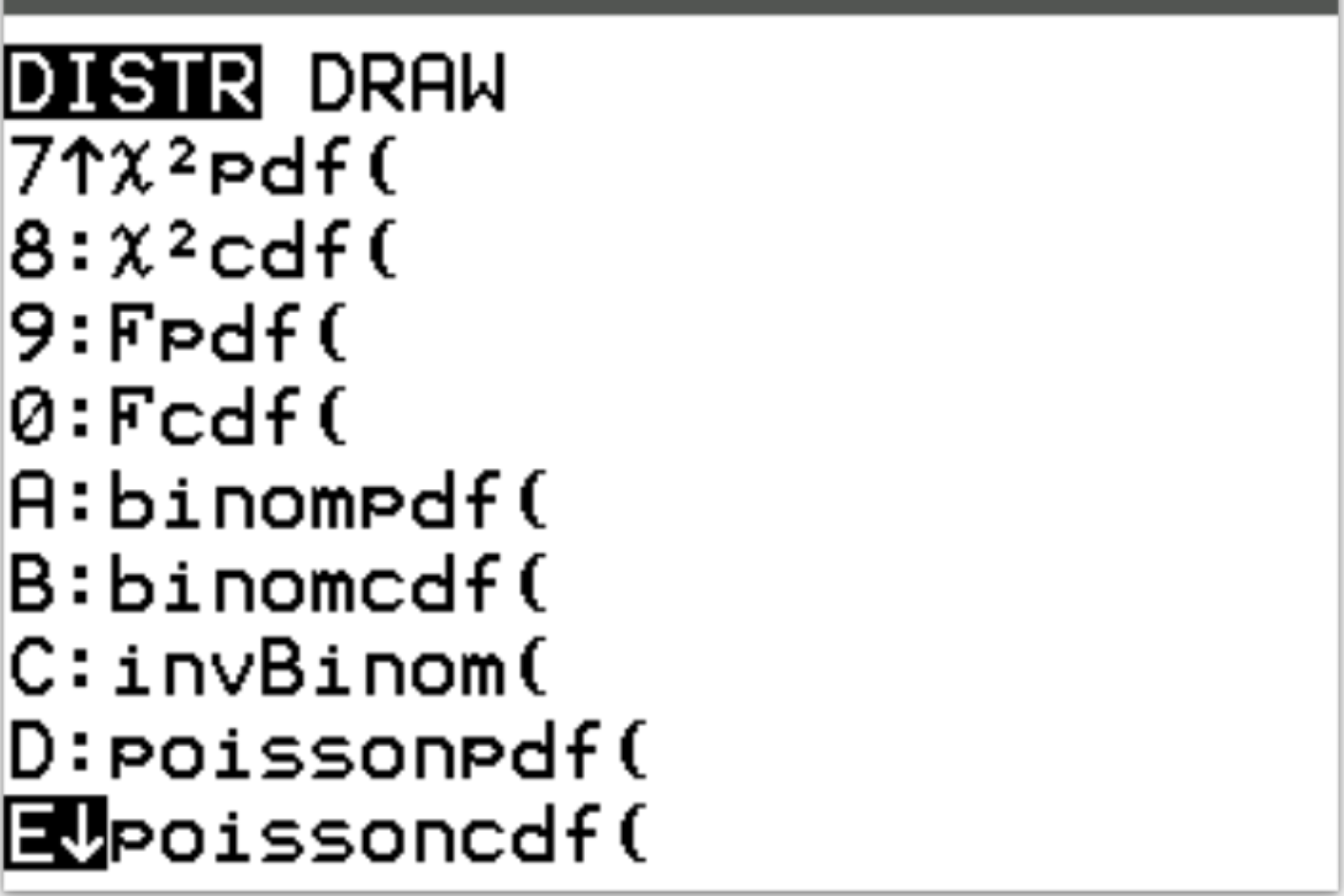
В следующих примерах показано, как использовать эти функции для ответа на различные вопросы.
Пример 1: Вероятность Пуассона ровно x успехов
Вопрос: Хозяйственный магазин продает в среднем 3 молотка в день. Какова вероятность того, что они продадут 5 молотков в данный день?
Ответ: Используйте функцию poissonpdf(mean, x):
пуассонpdf (3, 5) = 0,1008
Пример 2: Вероятность Пуассона меньше, чем x успехов
Вопрос: Хозяйственный магазин продает в среднем 3 молотка в день. Какова вероятность того, что они продадут менее 5 молотков в данный день?
Ответ: используйте функцию poissoncdf(mean, x-1):
пуассонкдф(3, 4) = 0,8153
Пример 3: Вероятность Пуассона не более чем x успехов
Вопрос: Хозяйственный магазин продает в среднем 3 молотка в день. Какова вероятность того, что они продадут не более 5 молотков в данный день?
Ответ: используйте функцию poissoncdf(mean, x):
пуассонкдф(3, 5) = 0,9161
Пример 4: Пуассоновская вероятность более чем x успехов
Вопрос: Хозяйственный магазин продает в среднем 3 молотка в день. Какова вероятность того, что они продадут более 5 молотков в данный день?
Ответ: Используйте функцию 1 – poissoncdf(mean, x):
1 – пуассонкдф(3, 5) = 0,0839
Пример 5: Вероятность Пуассона не менее x успехов
Вопрос: Хозяйственный магазин продает в среднем 3 молотка в день. Какова вероятность того, что они продадут не менее 5 молотков в данный день?
Ответ: используйте функцию 1 – poissoncdf(mean, x-1):
1 – пуассонкдф(3, 4) = 0,1847