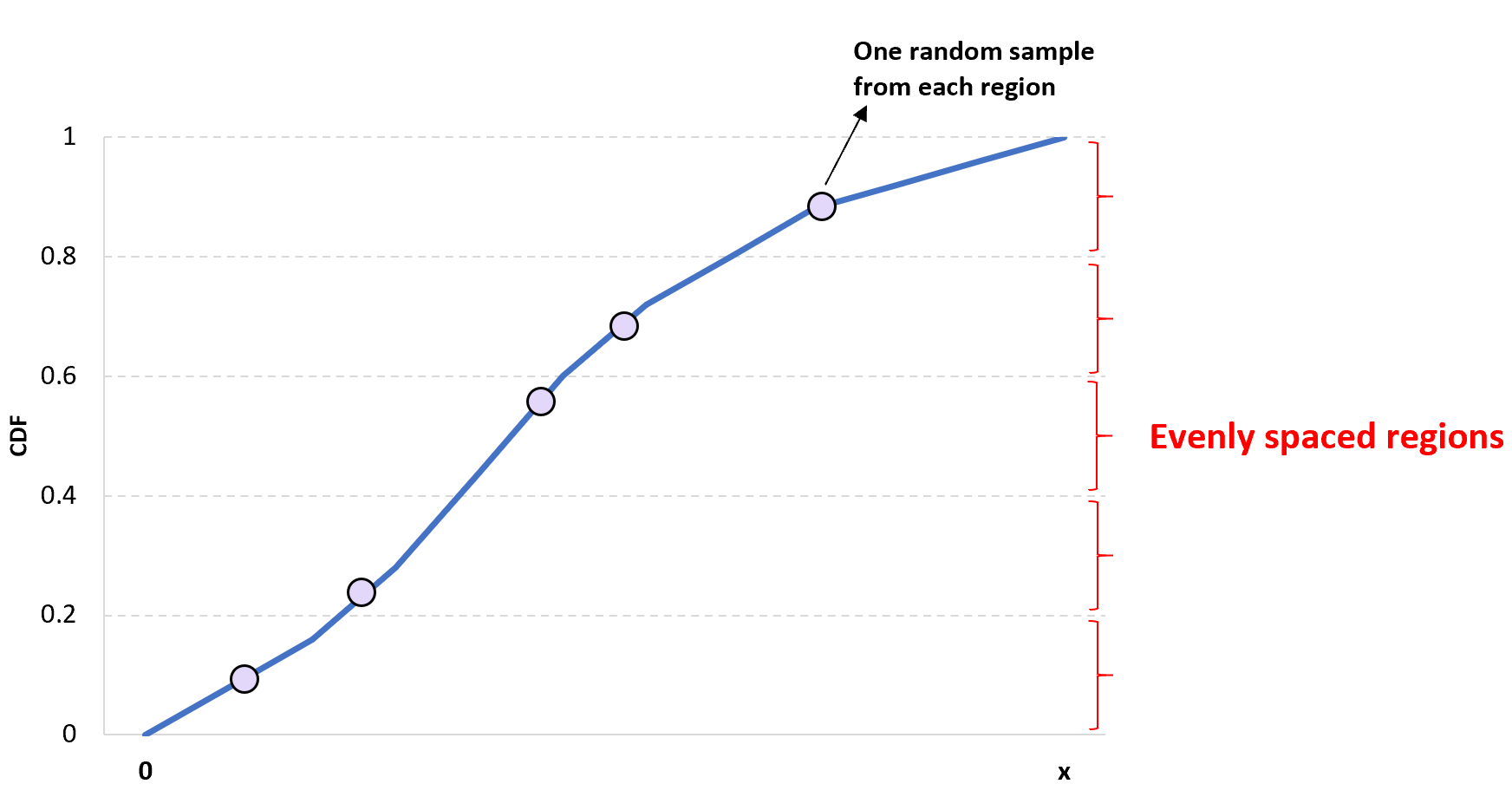
Выборка латинского гиперкуба - это метод, который можно использовать для выборки случайных чисел, в котором выборки равномерно распределены по пространству выборки.
Он широко используется для создания выборок, известных как контролируемые случайные выборки, и часто применяется в анализе методом Монте-Карло, поскольку позволяет значительно сократить количество симуляций, необходимых для получения точных результатов.
Вводный пример
Чтобы понять идею сэмплирования латинского гиперкуба, рассмотрим следующий простой пример:
Предположим, мы хотим получить выборку из 2 значений из набора данных, который нормально распределен со средним значением 0 и стандартным отклонением 1.
Если бы мы использовали настоящий генератор случайных чисел для получения этой выборки, возможно, что оба значения могли бы быть больше 0 или оба значения могли бы быть меньше 0.
Однако, если бы мы использовали выборку латинского гиперкуба для получения этой выборки, тогда было бы гарантировано, что одно значение будет больше 0, а другое меньше 0, потому что мы могли бы специально разделить пространство выборки на одну область со значениями выше 0 и одну область со значениями ниже 0, затем выберите случайную выборку из каждого региона.
Одномерная выборка латинского гиперкуба
Идея одномерной выборки латинского гиперкуба проста: разделить данный CDF на n различных областей и случайным образом выбрать одно значение из каждой области, чтобы получить выборку размера n .
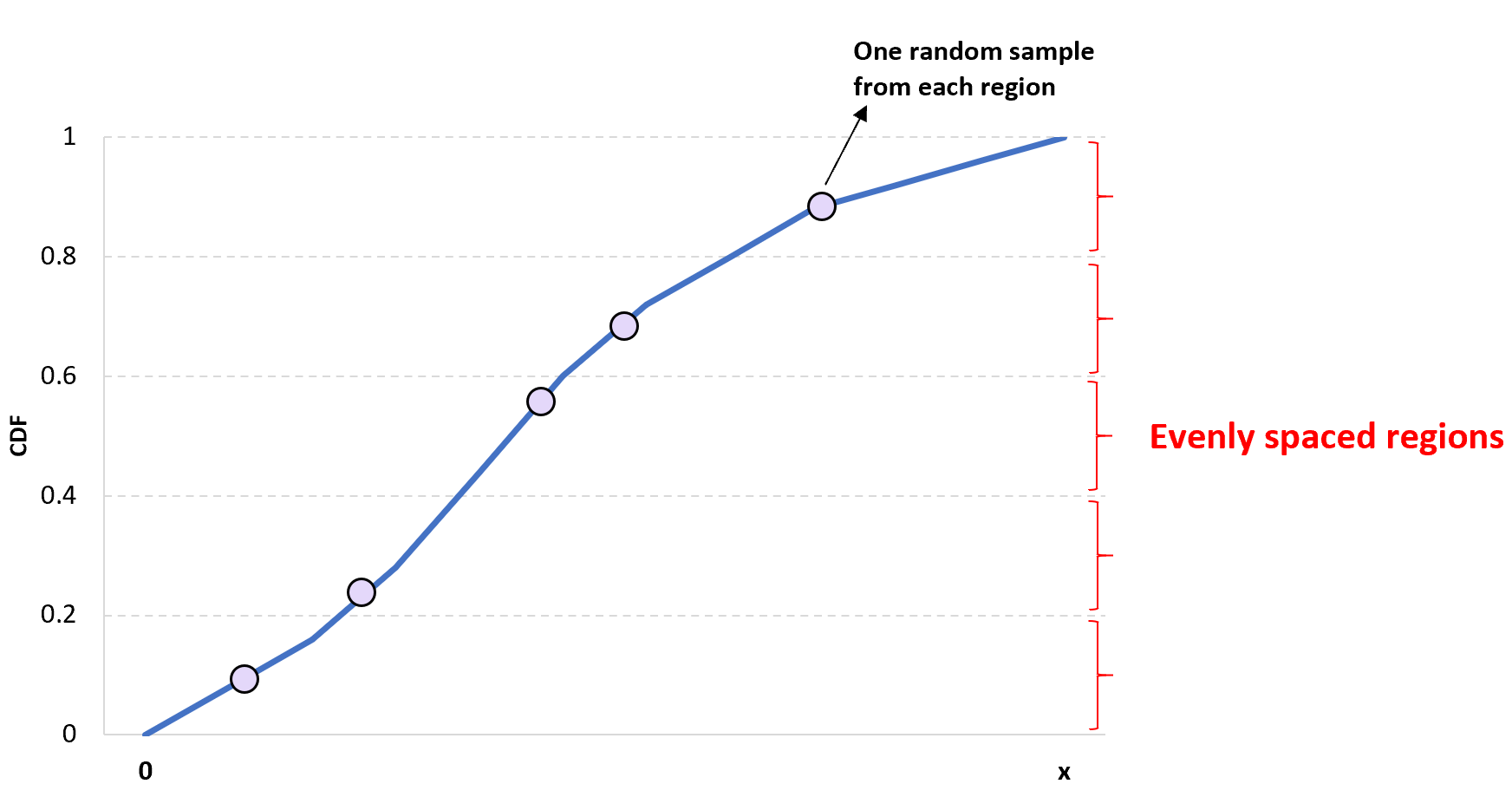
Преимущество этого подхода заключается в том, что он гарантирует включение в выборку хотя бы одного значения из каждого региона.
Двумерная выборка латинского гиперкуба
Мы можем легко распространить идею одномерной выборки латинского гиперкуба на два измерения.
Для двух переменных, x и y, мы можем разделить выборочное пространство каждой переменной на n равномерно расположенных областей и выбрать случайную выборку из каждого выборочного пространства, чтобы получить случайные значения в двух измерениях.
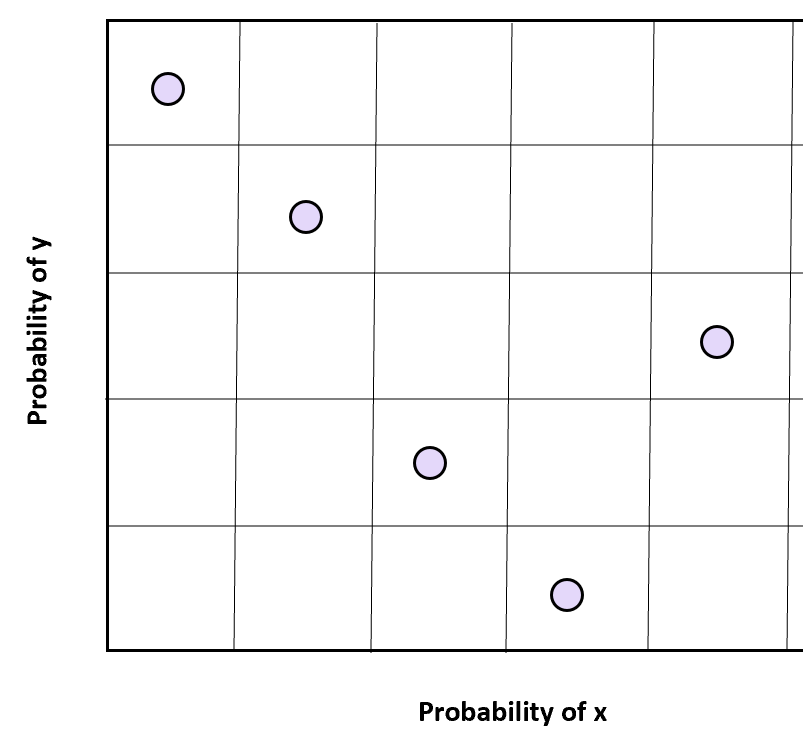
Важно отметить, что две переменные должны быть независимыми, чтобы этот метод выборки достиг желаемых результатов.
Выборка N-мерного латинского гиперкуба
Чтобы выполнить выборку латинского гиперкуба в больших измерениях, мы можем просто расширить идею двумерной выборки латинского гиперкуба на еще большее количество измерений.
Каждая переменная просто разбивается на равномерно расположенные области, а затем из каждой области выбираются случайные выборки для получения контролируемой случайной выборки.
Связанный: что такое многомерные данные?
Зачем использовать сэмплирование латинского гиперкуба?
Основное преимущество выборки латинского гиперкуба состоит в том, что она создает выборки, отражающие истинное лежащее в основе распределение, и обычно требует гораздо меньших размеров выборки, чем простая случайная выборка .
Этот метод выборки может быть особенно полезен, если вы работаете с данными, имеющими большое количество измерений, и вам необходимо получить случайные выборки, которые обязательно отразят истинное базовое распределение данных.