Функция lm() в R используется для подбора моделей линейной регрессии.
Эта функция использует следующий базовый синтаксис:
lm(формула, данные, …)
куда:
- формула: формула для линейной модели (например, y ~ x1 + x2)
- data: имя фрейма данных, содержащего данные
В следующем примере показано, как использовать эту функцию в R, чтобы сделать следующее:
- Соответствуйте модели регрессии
- Просмотр сводки по подбору регрессионной модели
- Просмотрите диагностические графики для модели
- Постройте подогнанную модель регрессии
- Делайте прогнозы, используя модель регрессии
Подходящая регрессионная модель
В следующем коде показано, как использовать функцию lm() для подбора модели линейной регрессии в R:
#define data
df = data.frame(x=c(1, 3, 3, 4, 5, 5, 6, 8, 9, 12),
y=c(12, 14, 14, 13, 17, 19, 22, 26, 24, 22))
#fit linear regression model using 'x' as predictor and 'y' as response variable
model <- lm(y ~ x, data=df)
Посмотреть сводку регрессионной модели
Затем мы можем использовать функцию summary() для просмотра сводки соответствия регрессионной модели:
#view summary of regression model
summary(model)
Call:
lm(formula = y ~ x, data = df)
Residuals:
Min 1Q Median 3Q Max
-4.4793 -0.9772 -0.4772 1.4388 4.6328
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 11.1432 1.9104 5.833 0.00039 \*\*\*
x 1.2780 0.2984 4.284 0.00267 \*\*
---
Signif. codes: 0 ‘\*\*\*’ 0.001 ‘\*\*’ 0.01 ‘\*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.929 on 8 degrees of freedom
Multiple R-squared: 0.6964, Adjusted R-squared: 0.6584
F-statistic: 18.35 on 1 and 8 DF, p-value: 0.002675
Вот как интерпретировать наиболее важные значения в модели:
- F-статистика = 18,35, соответствующее значение p = 0,002675. Поскольку это p-значение меньше 0,05, модель в целом является статистически значимой.
- Множественный R-квадрат = 0,6964. Это говорит нам о том, что 69,64% вариации переменной отклика y можно объяснить переменной-предиктором x.
- Коэффициентная оценка x : 1,2780. Это говорит нам о том, что каждое дополнительное увеличение x на одну единицу связано со средним увеличением y на 1,2780.
Затем мы можем использовать оценки коэффициентов из выходных данных, чтобы написать оценочное уравнение регрессии:
у = 11,1432 + 1,2780*(х)
Бонус : полное руководство по интерпретации каждого значения в выводе регрессии в R можно найти здесь .
Просмотрите диагностические графики модели
Затем мы можем использовать функцию plot() для построения диагностических графиков для регрессионной модели:
#create diagnostic plots
plot(model)
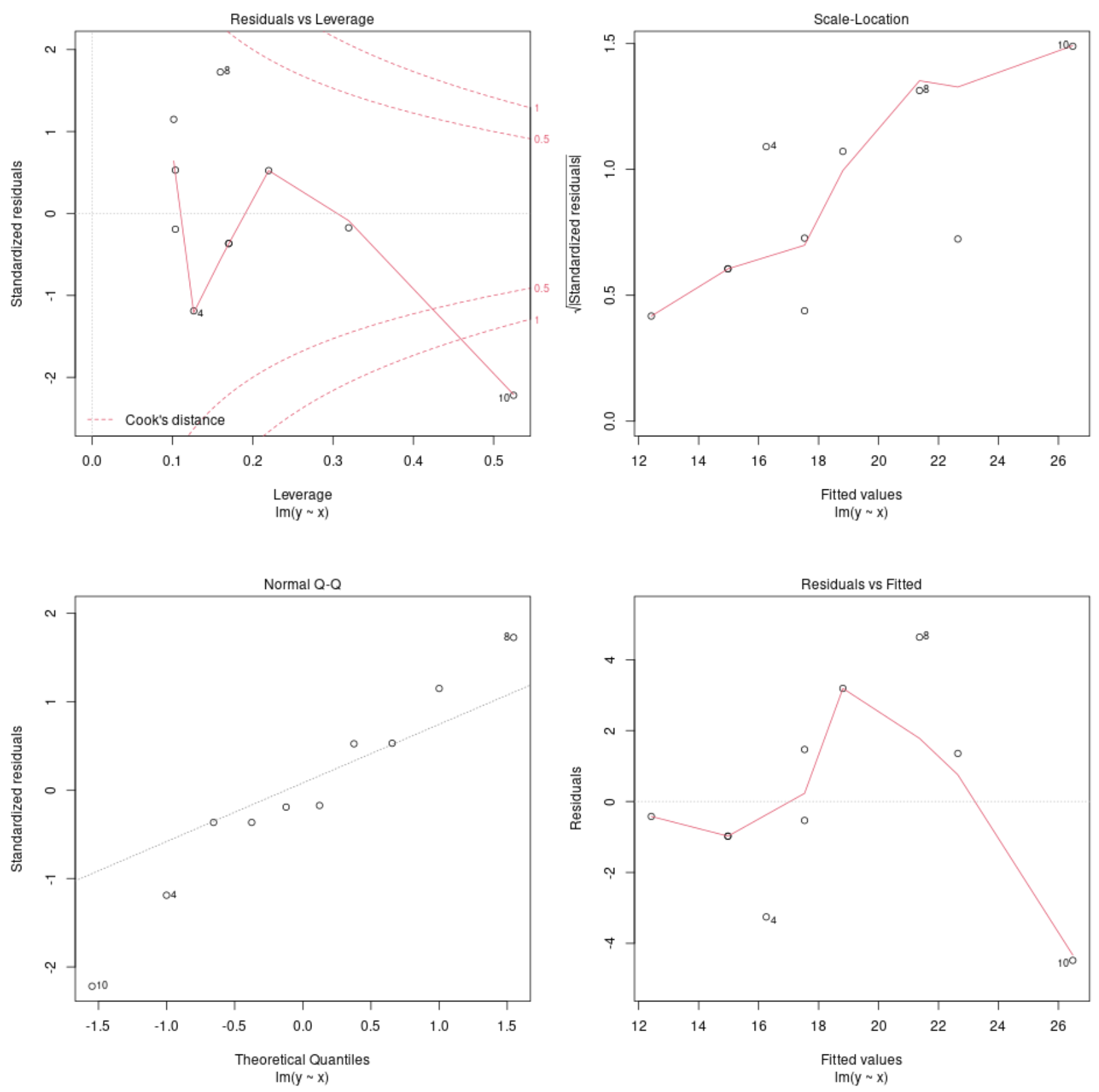
Эти графики позволяют нам анализировать остатки регрессионной модели, чтобы определить, подходит ли модель для использования с данными.
Обратитесь к этому руководству для полного объяснения того, как интерпретировать диагностические графики для модели в R.
Постройте подогнанную модель регрессии
Мы можем использовать функцию abline() для построения подобранной модели регрессии:
#create scatterplot of raw data
plot(df$x, df$y, col='red', main='Summary of Regression Model', xlab='x', ylab='y')
#add fitted regression line
abline(model)
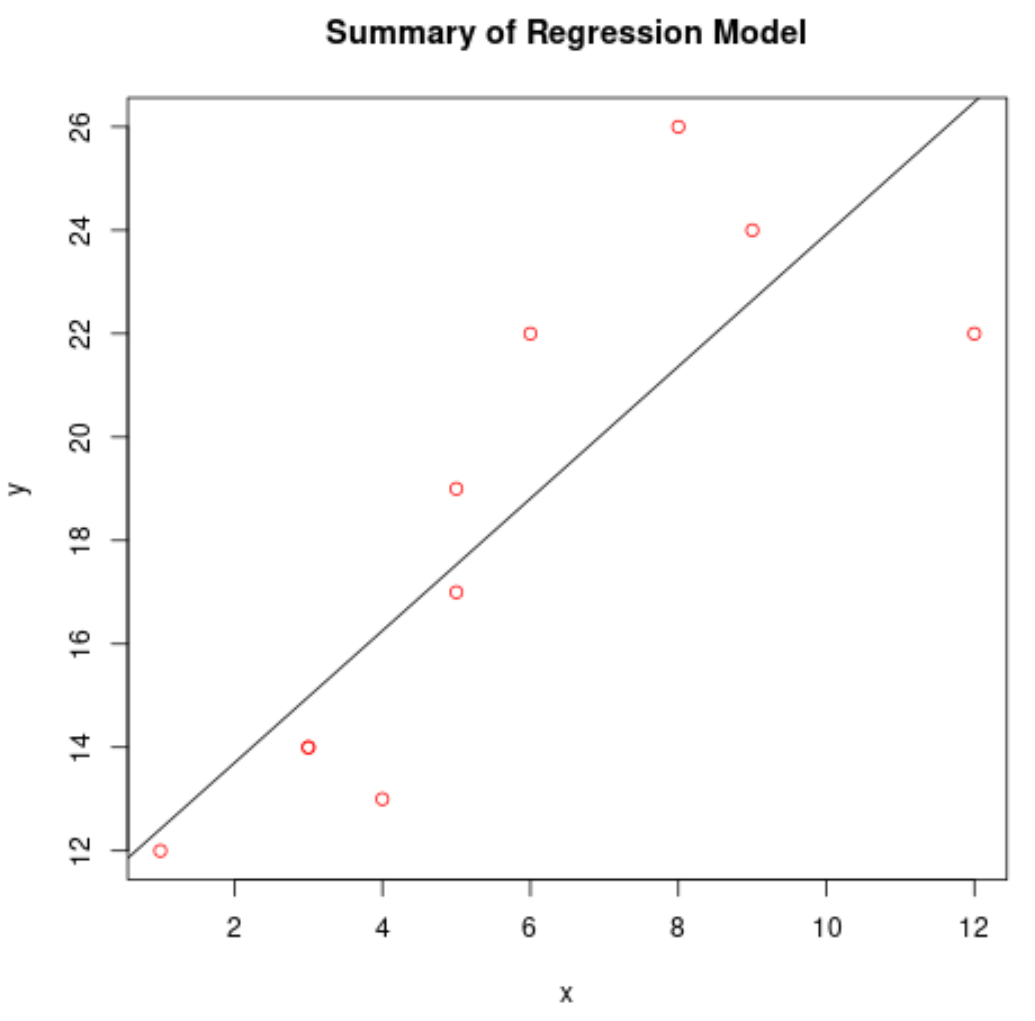
Используйте модель регрессии, чтобы делать прогнозы
Мы можем использовать функцию predict() , чтобы предсказать значение ответа для нового наблюдения:
#define new observation
new <- data.frame(x=c(5))
#use the fitted model to predict the value for the new observation
predict(model, newdata = new)
1
17.5332
Модель предсказывает, что это новое наблюдение будет иметь значение отклика 17,5332 .
Дополнительные ресурсы
Как выполнить простую линейную регрессию в R
Как выполнить множественную линейную регрессию в R
Как выполнить пошаговую регрессию в R