Модели регрессии используются для количественной оценки взаимосвязи между одной или несколькими переменными-предикторами и переменной отклика .
Всякий раз, когда мы подбираем регрессионную модель, мы хотим понять, насколько хорошо модель может использовать значения переменных-предикторов для прогнозирования значения переменной отклика.
Две метрики, которые мы часто используем для количественной оценки того, насколько хорошо модель соответствует набору данных, — это средняя абсолютная ошибка (MAE) и среднеквадратическая ошибка (RMSE), которые рассчитываются следующим образом:
MAE : метрика, которая сообщает нам среднюю абсолютную разницу между прогнозируемыми значениями и фактическими значениями в наборе данных. Чем ниже MAE, тем лучше модель соответствует набору данных.
MAE = 1/n * Σ|y i – ŷ i |
куда:
- Σ — это символ, который означает «сумма»
- y i - наблюдаемое значение для i -го наблюдения
- ŷ i - прогнозируемое значение для i -го наблюдения
- n - размер выборки
RMSE : метрика, которая сообщает нам квадратный корень из средней квадратичной разницы между прогнозируемыми значениями и фактическими значениями в наборе данных. Чем ниже RMSE, тем лучше модель соответствует набору данных.
Он рассчитывается как:
СКО = √ Σ(y i – ŷ i ) 2 / n
куда:
- Σ — это символ, который означает «сумма»
- ŷ i - прогнозируемое значение для i -го наблюдения
- y i - наблюдаемое значение для i -го наблюдения
- n - размер выборки
Пример: Расчет RMSE и MAE
Предположим, мы используем регрессионную модель, чтобы предсказать количество очков, которое 10 игроков наберут в баскетбольном матче.
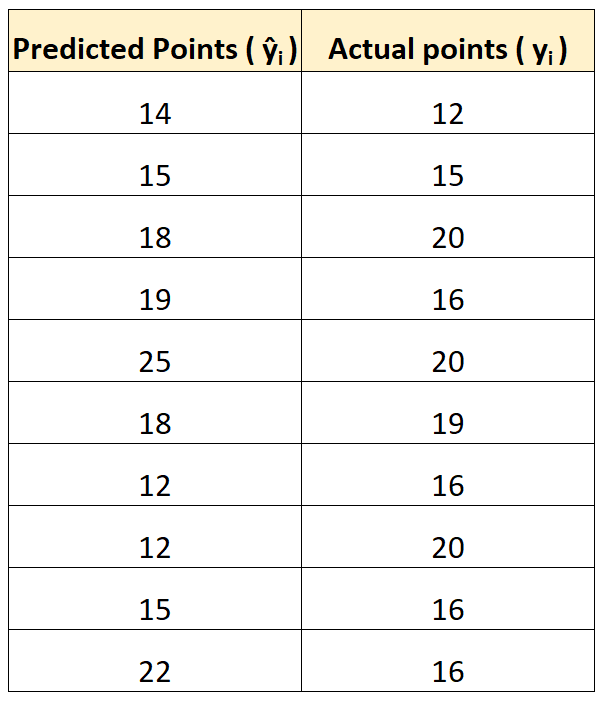
В следующей таблице показаны прогнозируемые очки по модели и фактические очки, набранные игроками:

Используя калькулятор MAE , мы можем рассчитать MAE как 3,2.
Это говорит нам о том, что средняя абсолютная разница между прогнозируемыми значениями модели и фактическими значениями составляет 3,2.
Используя Калькулятор RMSE , мы можем рассчитать RMSE, чтобы он был равен 4 .
Это говорит нам о том, что квадратный корень из среднеквадратичной разницы между предсказанными набранными очками и фактическими набранными очками равен 4.
Обратите внимание, что каждая метрика дает нам представление о типичной разнице между прогнозируемым значением, сделанным моделью, и фактическим значением в наборе данных, но интерпретация каждой метрики немного отличается.
RMSE против MAE: какую метрику следует использовать?
Если вы хотите придать больший вес наблюдениям, которые находятся дальше от среднего (т. е. если «отклонение» на 20 более чем в два раза хуже, чем отклонение на 10 дюймов), то лучше использовать RMSE для измерения ошибки, потому что RMSE более чувствителен к наблюдениям, которые далеки от среднего.
Однако, если «выключиться» в 20 раз хуже, чем в 10, то лучше использовать MAE.
Чтобы проиллюстрировать это, предположим, что у нас есть один игрок, который явно отличается по количеству набранных очков:

Используя онлайн-калькуляторы, упомянутые ранее, мы можем рассчитать MAE и RMSE следующим образом:
- МАЭ : 8
- Среднеквадратичное значение : 16,4356
Обратите внимание, что RMSE увеличивается намного больше, чем MAE.
Это связано с тем, что в формуле RMSE используются квадраты разницы, а квадрат разницы между наблюдаемым значением 76 и прогнозируемым значением 22 довольно велик. Это приводит к значительному увеличению значения RMSE.
На практике мы обычно подгоняем несколько моделей регрессии к набору данных и вычисляем только одну из этих метрик для каждой модели.
Например, мы можем подобрать три разные регрессионные модели и рассчитать RMSE для каждой модели. Затем мы выберем модель с самым низким значением RMSE в качестве «лучшей» модели, потому что именно она делает прогнозы, наиболее близкие к фактическим значениям из набора данных.
В любом случае просто убедитесь, что вы вычисляете одну и ту же метрику для каждой модели. Например, не рассчитывайте MAE для одной модели и RMSE для другой модели, а затем сравнивайте эти две метрики.
Дополнительные ресурсы
В следующих руководствах объясняется, как рассчитать MAE с помощью различных статистических программ:
Как рассчитать среднюю абсолютную ошибку в Excel
Как рассчитать среднюю абсолютную ошибку в R
Как рассчитать среднюю абсолютную ошибку в Python
В следующих руководствах объясняется, как рассчитать RMSE с помощью различных статистических программ:
Как рассчитать среднеквадратичную ошибку в Excel
Как рассчитать среднеквадратичную ошибку в R
Как рассчитать среднеквадратичную ошибку в Python