Распределение вероятностей говорит нам о вероятности того, что случайная величина примет определенные значения.
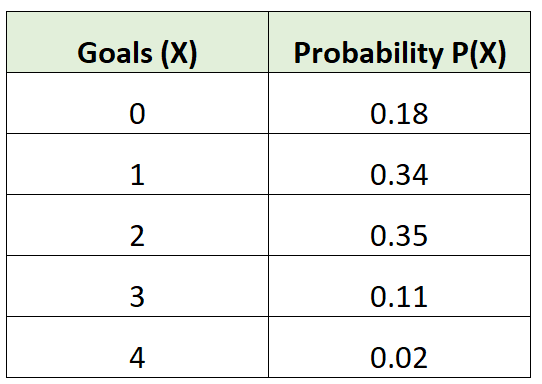
Например, следующее распределение вероятностей говорит нам о вероятности того, что определенная футбольная команда забьет определенное количество голов в данной игре:
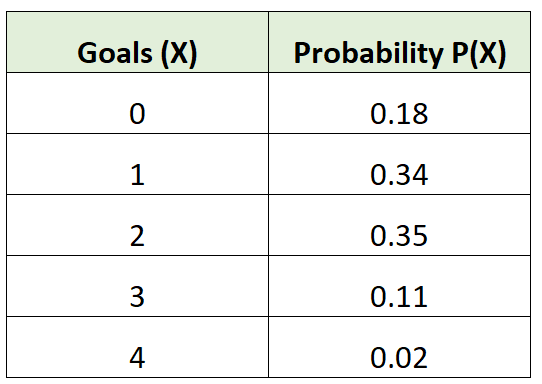
Примечание.Вероятности в действительном распределении вероятностей всегда будут в сумме равны 1. Мы можем подтвердить, что это распределение вероятностей действительно: 0,18 + 0,34 + 0,35 + 0,11 + 0,02 = 1.
Чтобы найти среднее (иногда называемое «ожидаемым значением») любого распределения вероятностей, мы можем использовать следующую формулу:
Mean (Or "Expected Value") of a Probability Distribution:
μ = Σx \* P(x)
where:
•x: Data value
•P(x): Probability of value
Например, рассмотрим наше распределение вероятностей для футбольной команды:

Среднее количество голов для футбольной команды будет рассчитываться как:
μ = 0*0,18 + 1*0,34 + 2*0,35 + 3*0,11 + 4*0,02 = 1,45 гола.
В следующих примерах показано, как вычислить среднее значение распределения вероятностей в нескольких других сценариях.
Пример 1: Среднее количество отказов транспортных средств
Следующее распределение вероятностей говорит нам о вероятности того, что данное транспортное средство испытает определенное количество отказов батареи в течение 10-летнего периода:
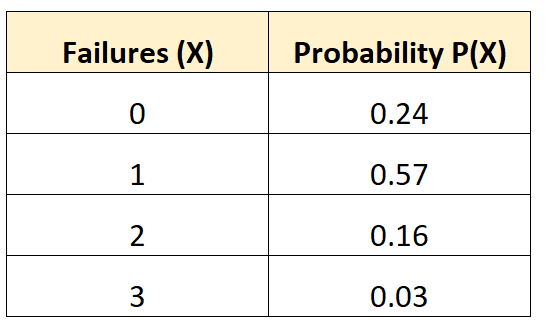
Вопрос: Каково среднее количество ожидаемых отказов для этого автомобиля?
Решение.Среднее количество ожидаемых отказов рассчитывается как:
μ = 0*0,24 + 1*0,57 + 2*0,16 + 3*0,03 = 0,98 отказов.
Пример 2: Среднее количество побед
Следующее распределение вероятностей говорит нам о вероятности того, что данная баскетбольная команда выиграет определенное количество игр в турнире:
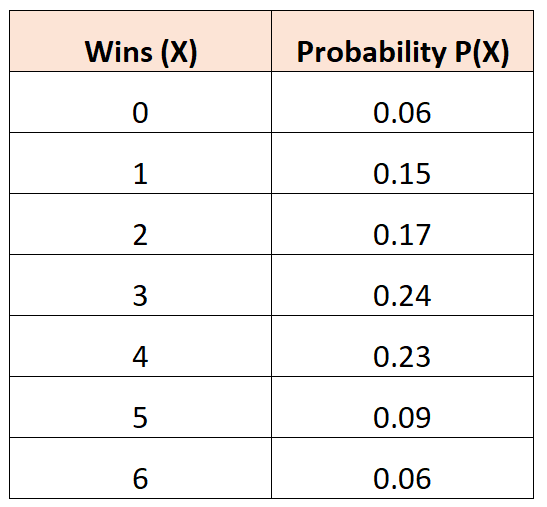
Вопрос: Каково среднее количество ожидаемых побед для этой команды?
Решение: Среднее количество ожидаемых выигрышей рассчитывается как:
μ = 0*0,06 + 1*0,15 + 2*0,17 + 3*0,24 + 4*0,23 + 5*0,09 + 6*0,06 = 2,94 победы.
Пример 3: Среднее количество продаж
Следующее распределение вероятностей говорит нам о вероятности того, что данный продавец совершит определенное количество продаж в предстоящем месяце:
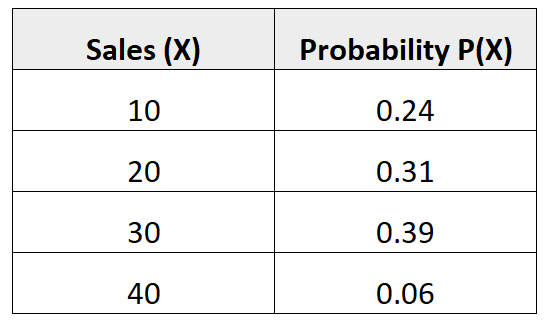
Вопрос: Каково среднее количество ожидаемых продаж этого продавца в предстоящем месяце?
Решение: Среднее количество ожидаемых продаж рассчитывается как:
μ = 10*0,24 + 20*0,31 + 30*0,39 + 40*0,06 = 22,7 продаж.
Бонус: калькулятор распределения вероятностей
Вы можете использовать этот калькулятор для автоматического расчета среднего значения любого распределения вероятностей.