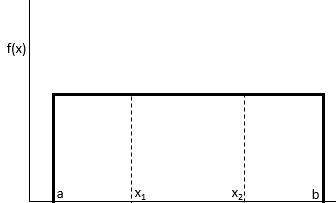
Равномерное распределение — это такое распределение вероятностей, при котором каждое значение в интервале от a до b будет выбрано с равной вероятностью.
Вероятность того, что мы получим значение между x 1 и x 2 на интервале от a до b , можно найти по формуле:
P(получить значение между x 1 и x 2 ) = (x 2 – x 1 ) / (b – a)
В этом руководстве объясняется, как найти оценку максимального правдоподобия (mle) для параметров a и b равномерного распределения.
Оценка максимального правдоподобия
Шаг 1: Напишите функцию правдоподобия.
Для равномерного распределения функция правдоподобия может быть записана как:
Шаг 2: Напишите функцию логарифмического правдоподобия.
Шаг 3: Найдите значения для a и b , которые максимизируют логарифмическое правдоподобие, взяв производную функции логарифмического правдоподобия по отношению к a и b .
Производная логарифмической функции правдоподобия по a может быть записана как:
Точно так же производная логарифмической функции правдоподобия по b может быть записана как:
Шаг 4: Определите оценщики максимального правдоподобия для a и b.
Обратите внимание, что производная по а монотонно возрастает. Таким образом, mle для а будет максимально возможным, что будет просто равно:
мин(Х 1 , Х 2 , … , Х п )
Также обратите внимание, что производная по b монотонно убывает. Таким образом, mle для b будет наименьшим из возможных b , который будет равен:
макс(Х 1 , Х 2 , … , Х п )