Одним из способов количественной оценки связи между двумя переменными является использованиекоэффициента корреляции Пирсона , который является мерой линейной связи между двумя переменными . Он всегда принимает значение от -1 до 1, где:
- -1 указывает на совершенно отрицательную линейную корреляцию между двумя переменными
- 0 указывает на отсутствие линейной корреляции между двумя переменными
- 1 указывает на совершенно положительную линейную корреляцию между двумя переменными.
Чтобы определить, является ли коэффициент корреляции статистически значимым, можно рассчитать соответствующий t-показатель и p-значение.
Формула для расчета t-показателя коэффициента корреляции (r):
т = г √ (п-2) / √ (1-г 2 )
Значение p рассчитывается как соответствующее двустороннее значение p для t-распределения с n-2 степенями свободы.
P-значение для коэффициента корреляции в Excel
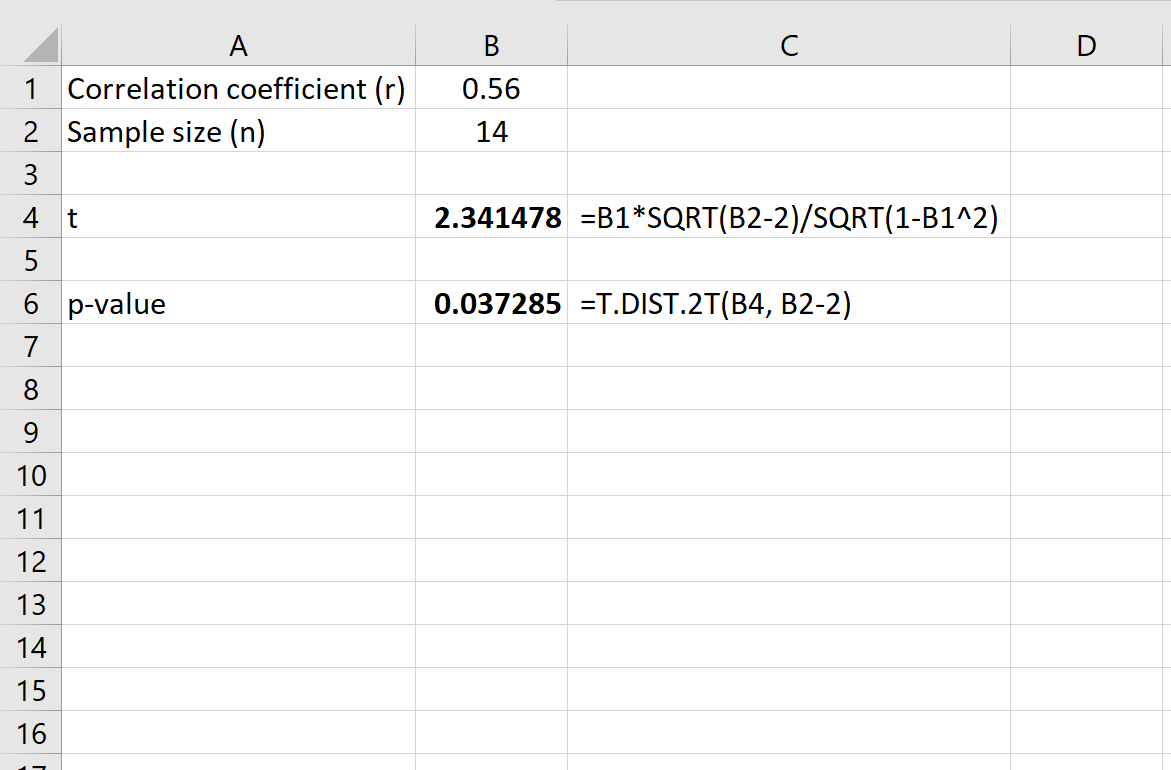
Следующие формулы показывают, как рассчитать значение p для заданного коэффициента корреляции и размера выборки в Excel:
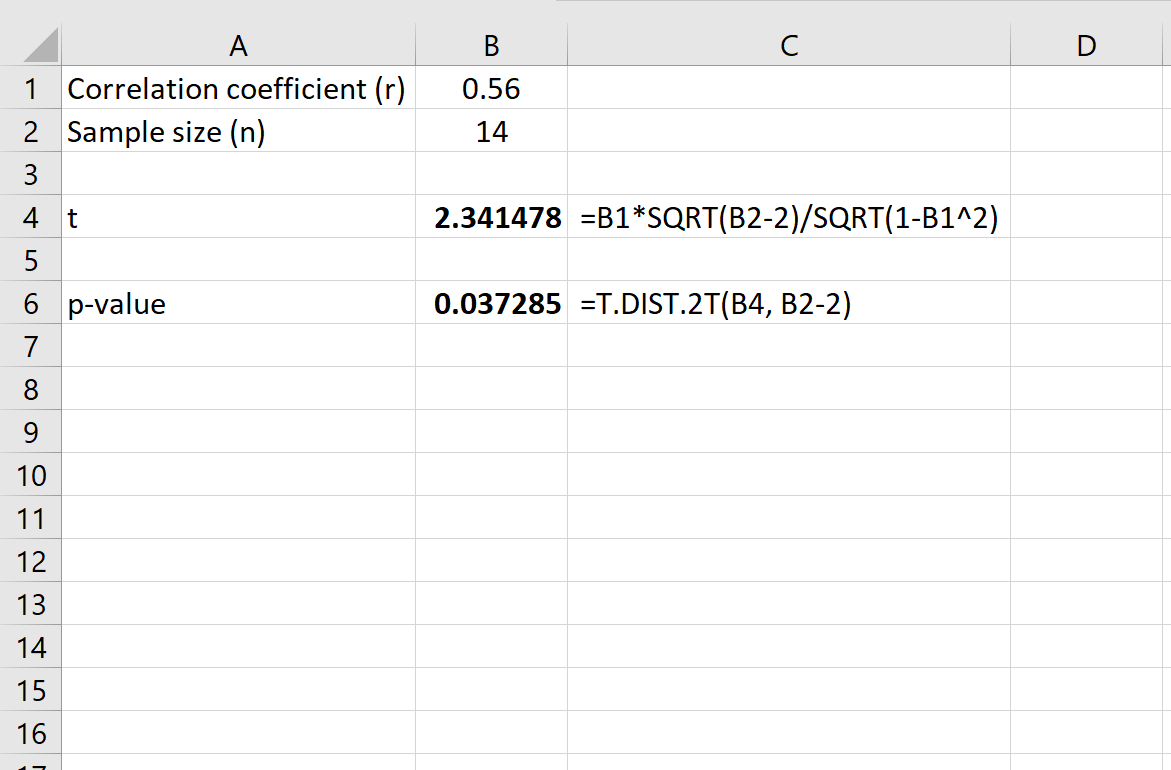
Для коэффициента корреляции r = 0,56 и размера выборки n = 14 мы находим, что:
- t-балл: 2,341478
- р-значение: 0,037285
Напомним, что для корреляционного теста у нас есть следующие нулевая и альтернативная гипотезы:
Нулевая гипотеза (H 0 ): корреляция между двумя переменными равна нулю.
Альтернативная гипотеза: (Ha): корреляция между двумя переменными не равна нулю, например, существует статистически значимая корреляция.
Если мы используем уровень значимости α = 0,05, то в этом случае мы отклоним нулевую гипотезу, поскольку значение p (0,037285) меньше 0,05. Можно сделать вывод, что коэффициент корреляции статистически значим.