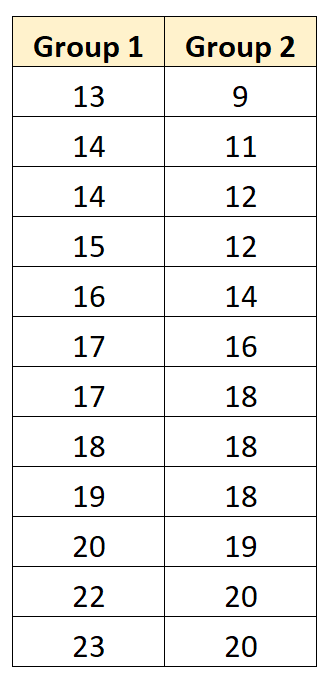
Стьюдентный критерий для парных выборок используется для сравнения средних значений двух выборок, когда каждое наблюдение в одной выборке может быть сопоставлено с наблюдением в другой выборке.
В следующем пошаговом примере показано, как выполнить t-критерий парных выборок, чтобы определить, равны ли средние значения генеральной совокупности между следующими двумя группами:
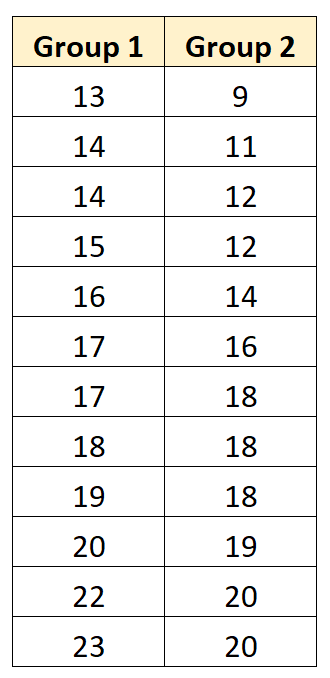
Шаг 1: Рассчитайте тестовую статистику
Тестовая статистика парного t-теста рассчитывается как:
t = x diff / (s diff /√ n )
куда:
- x diff : выборочное среднее различий
- s: выборочное стандартное отклонение различий
- n: размер выборки (т.е. количество пар)
Мы рассчитаем среднее значение различий между двумя группами и стандартное отклонение различий между двумя группами:
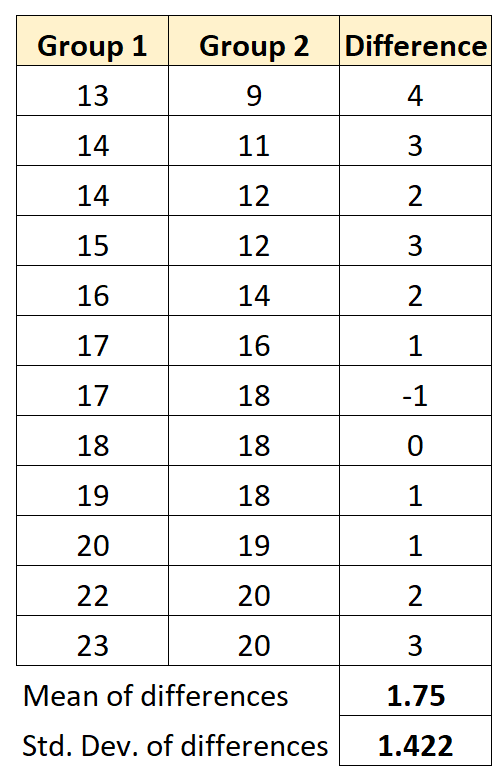
Таким образом, наша тестовая статистика может быть рассчитана как:
- t = x diff / (s diff /√ n )
- т = 1,75 / (1,422/√ 12 )
- т = 4,26
Шаг 2: Рассчитайте критическое значение
Далее нам нужно найти критическое значение, с которым можно сравнить нашу тестовую статистику.
В этом примере мы будем использовать двусторонний критерий с α = 0,05 и df = n-1 степеней свободы.
Согласно таблице t-Distribution критическое значение, соответствующее этим значениям, равно 2,201 :
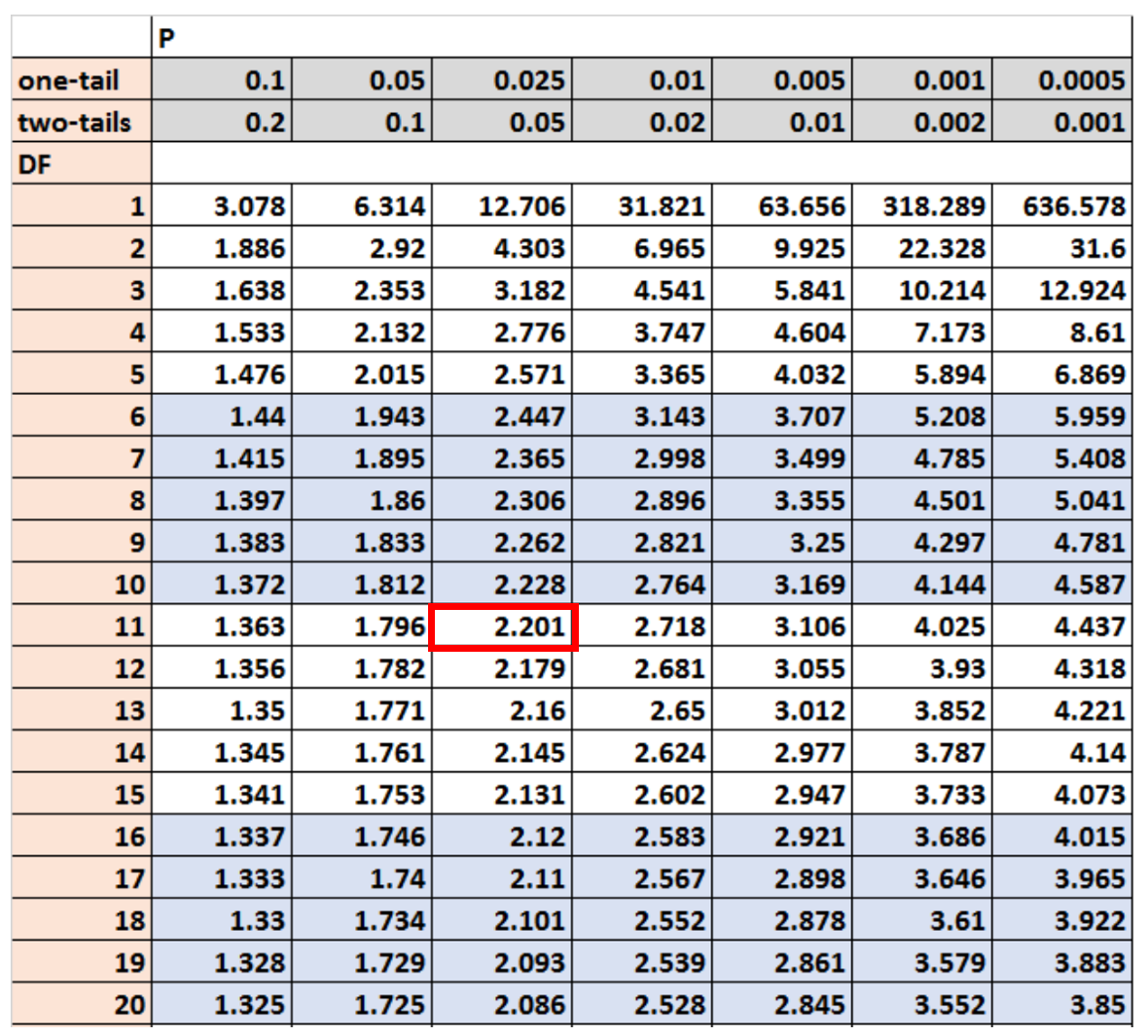
Шаг 3: Отклонить или не отклонить нулевую гипотезу
Наш t-тест для парных выборок использует следующую нулевую и альтернативную гипотезы:
- H 0 : µ 1 = µ 2 (средние значения двух популяций равны)
- H A : µ 1 ≠ µ 2 (две средние значения совокупности не равны)
Поскольку абсолютное значение нашей тестовой статистики ( 4.26 ) больше критического значения, найденного в t-таблице ( 2.201 ), мы отклоняем нулевую гипотезу.
Это означает, что у нас есть достаточно доказательств, чтобы сказать, что среднее значение между двумя группами не равно.
Бонус: не стесняйтесь использовать калькулятор t-критерия для парных выборок, чтобы подтвердить свои результаты.