В статистике мы часто используемкоэффициент корреляции Пирсона для измерения линейной зависимости между двумя переменными. Однако иногда нам интересно понять взаимосвязь между двумя переменными , контролируя при этом третью переменную .
Например, предположим, что мы хотим измерить связь между количеством часов, отработанных учащимся, и полученной им итоговой оценкой на экзамене, контролируя текущую оценку учащегося в классе. В этом случае мы могли бы использовать частичную корреляцию для измерения взаимосвязи между часами обучения и итоговой оценкой на экзамене.
В этом руководстве объясняется, как рассчитать частичную корреляцию в Excel.
Пример: Частичная корреляция в Excel
Предположим, у нас есть набор данных, который показывает следующую информацию для 10 студентов:
- Текущая оценка в классе
- Количество часов, потраченных на подготовку к выпускному экзамену
- Итоговый балл за экзамен
Используйте следующие шаги, чтобы найти частичную корреляцию между часами обучения и экзаменационными баллами при контроле текущей оценки.
Шаг 1: Рассчитайте каждую попарную корреляцию.
Во-первых, мы рассчитаем корреляцию между каждой парной комбинацией переменных:
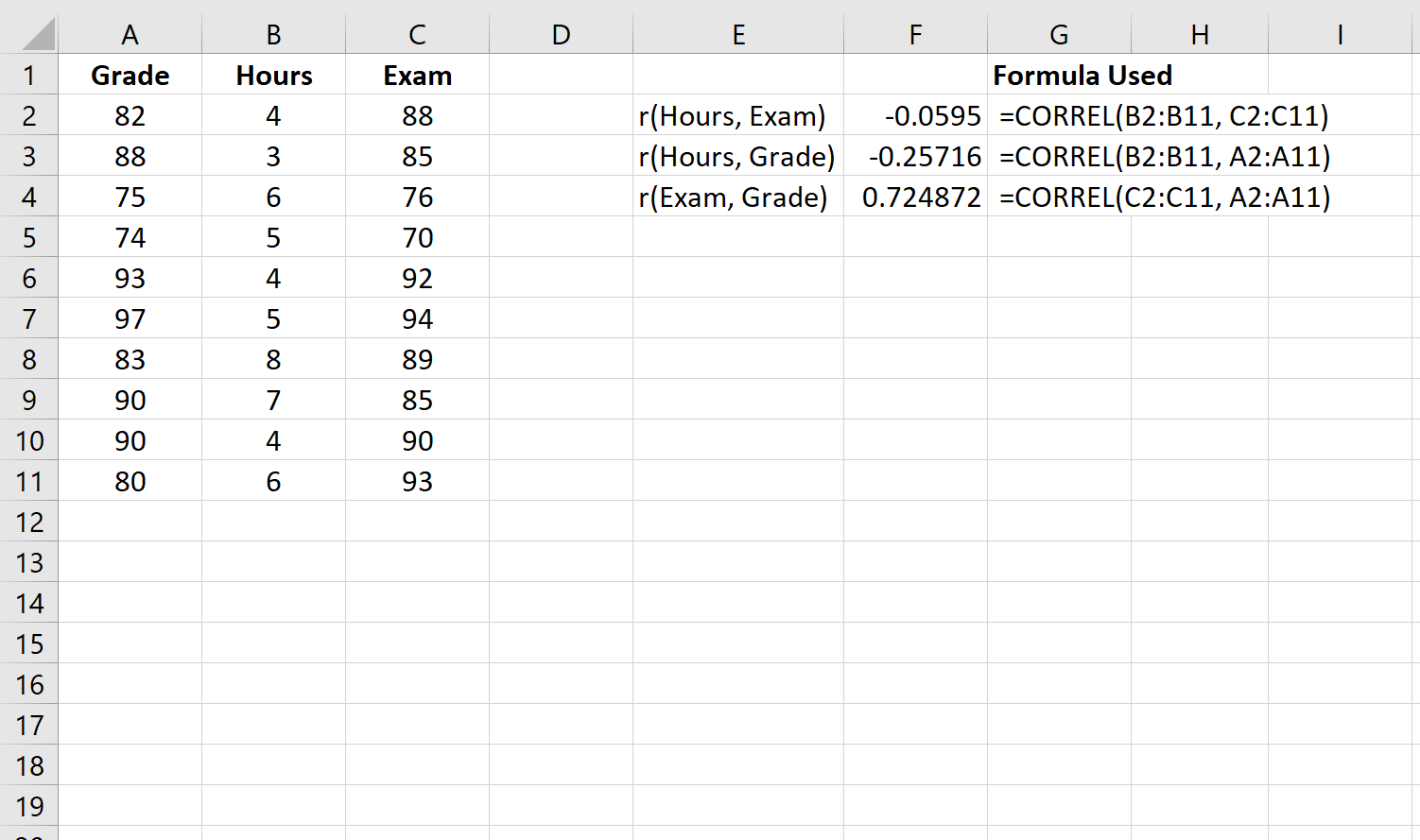
Шаг 2: Рассчитайте частичную корреляцию между часами и экзаменационным баллом.
Формула для расчета частичной корреляции между переменной A и переменной B при контроле переменной C выглядит следующим образом:
Частная корреляция = (r A,B – r A,C *r B,C ) / √((1-r 2 A,B )(1-r 2 B,C ))
На следующем снимке экрана показано, как использовать эту формулу для расчета частичной корреляции между часами и экзаменационным баллом с учетом текущей оценки:
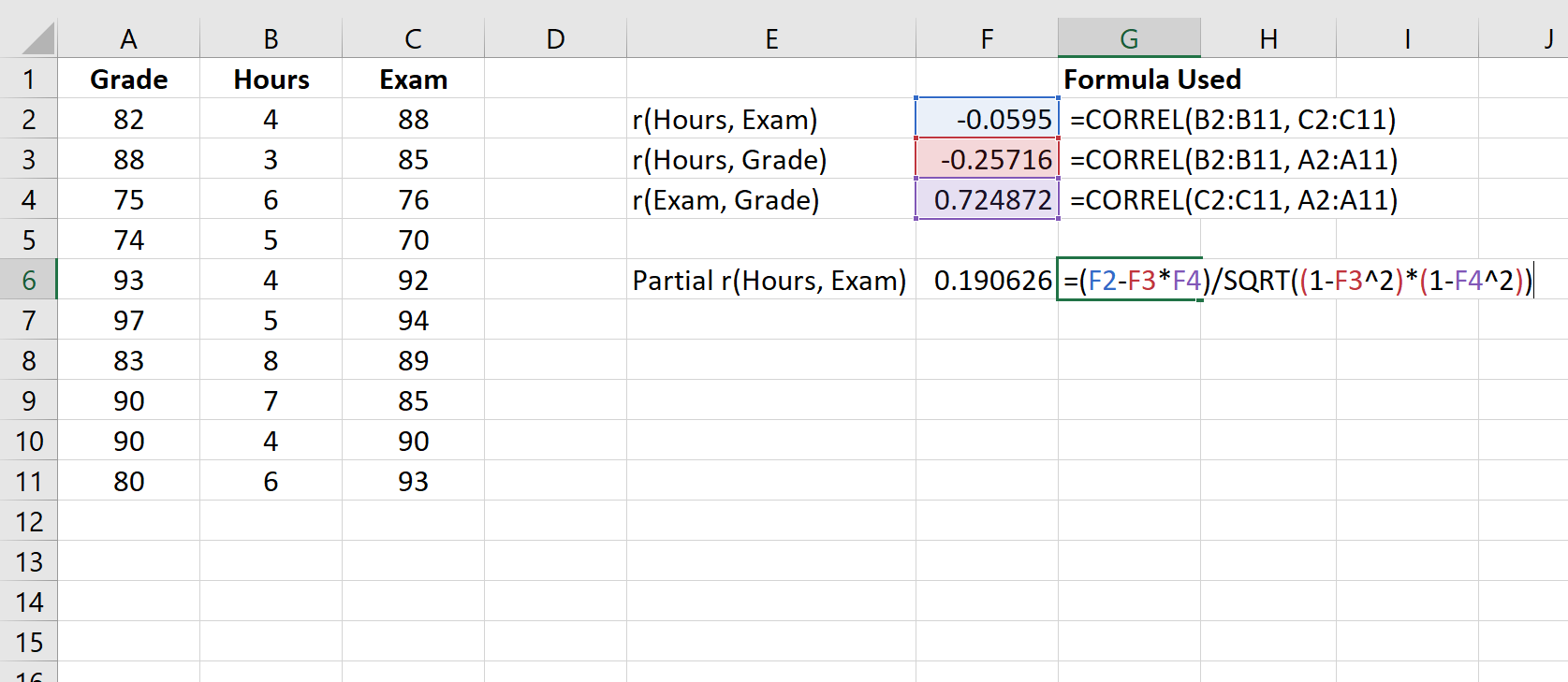
Частная корреляция составляет 0,190626.Чтобы определить, является ли эта корреляция статистически значимой, мы можем найти соответствующее значение p.
Шаг 3: Рассчитайте p-значение частной корреляции.
Тестовая статистика t может быть рассчитана как:
т = г √ (n-3) / √ (1-г 2 )
На следующем снимке экрана показано, как использовать эту формулу для расчета статистики теста и соответствующего значения p:
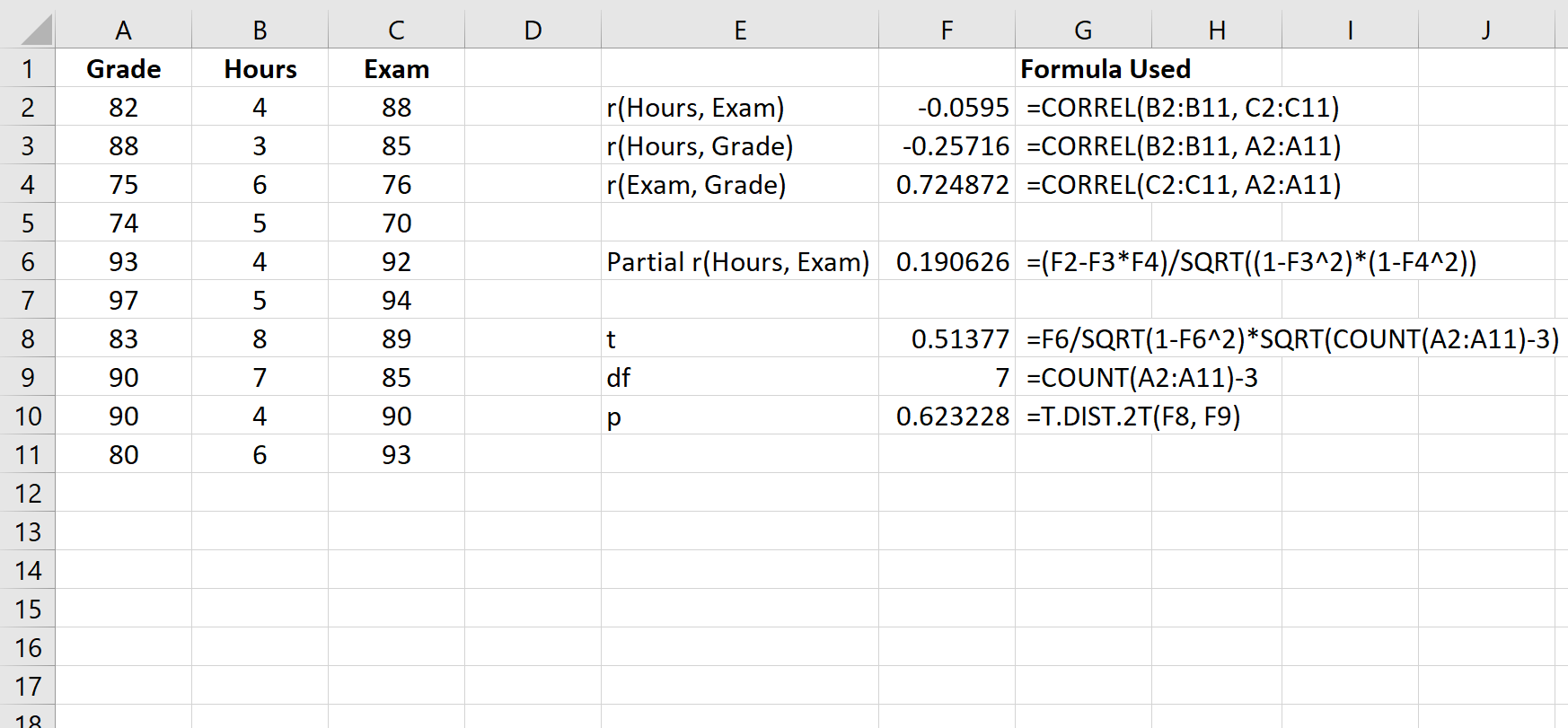
Тестовая статистика t равна 0,51377.Всего степеней свободы n-3 = 10-3 = 7.Соответствующее значение p равно 0,623228.Поскольку это значение не меньше 0,05, это означает, что частичная корреляция между часами и экзаменационным баллом не является статистически значимой.