Коэффициент фи (иногда называемый среднеквадратичным коэффициентом непредвиденных обстоятельств ) является мерой связи между двумя бинарными переменными.
Для данной таблицы 2 × 2 для двух случайных величин x и y :

Коэффициент Фи можно рассчитать как:
Φ = (AD-BC) / √ (A+B)(C+D)(A+C)(B+D)
Пример. Расчет коэффициента Фи
Предположим, мы хотим знать, связан ли пол с предпочтениями политической партии. Мы берем простую случайную выборку из 25 избирателей и опрашиваем их об их предпочтениях в отношении политических партий. В следующей таблице представлены результаты опроса:
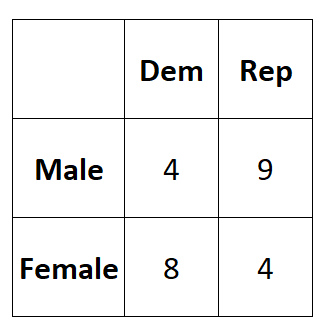
Мы можем рассчитать коэффициент Фи между двумя переменными как:
Φ = (4*4-9*8) / √ (4+9)(8+4)(4+8)(9+4) = (16-72)/√ 24336 = -0,3589
Примечание. Мы также могли бы рассчитать это с помощью Калькулятора коэффициента Фи .
Как интерпретировать коэффициент Фи
Подобно коэффициенту корреляции Пирсона, коэффициент Фи принимает значения от -1 до 1, где:
- -1 указывает на совершенно отрицательную связь между двумя переменными.
- 0 указывает на отсутствие связи между двумя переменными.
- 1 указывает на совершенно положительную связь между двумя переменными.
Как правило, чем дальше коэффициент Фи от нуля, тем сильнее связь между двумя переменными.
Другими словами, чем дальше коэффициент Фи от нуля, тем больше свидетельств того, что между двумя переменными существует какая-то систематическая закономерность.
Дополнительные ресурсы
Руководство по коэффициенту корреляции Пирсона
Руководство по точному тесту Фишера
Руководство по критерию независимости хи-квадрат


