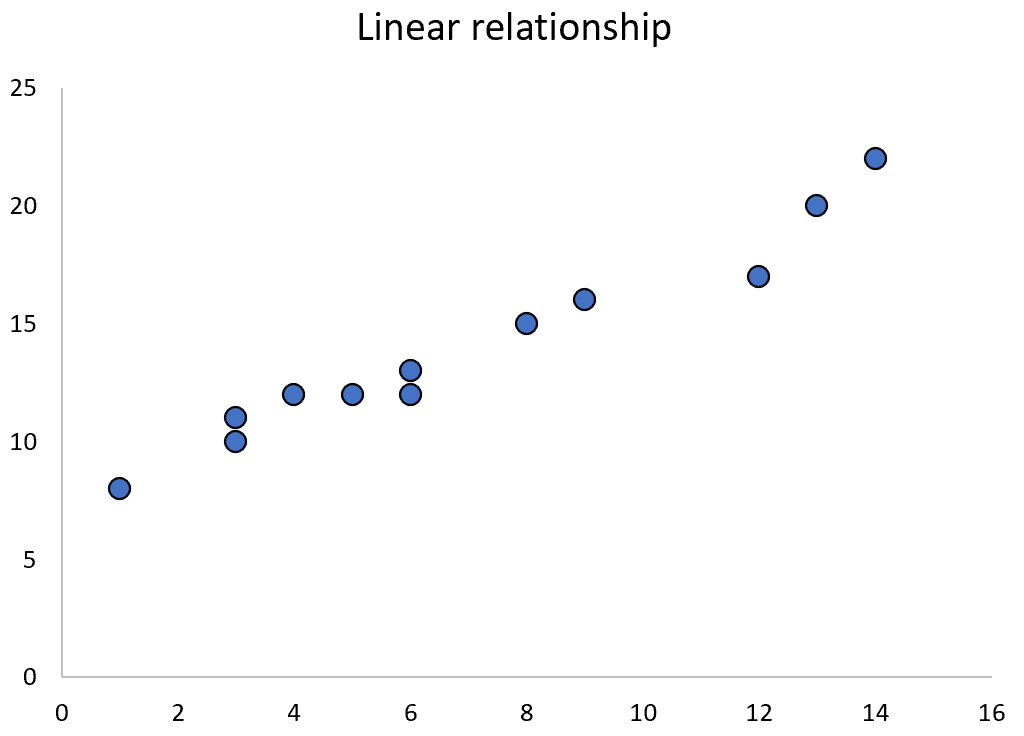
Когда две переменные имеют линейную связь, мы часто можем использовать простую линейную регрессию для количественной оценки их связи.
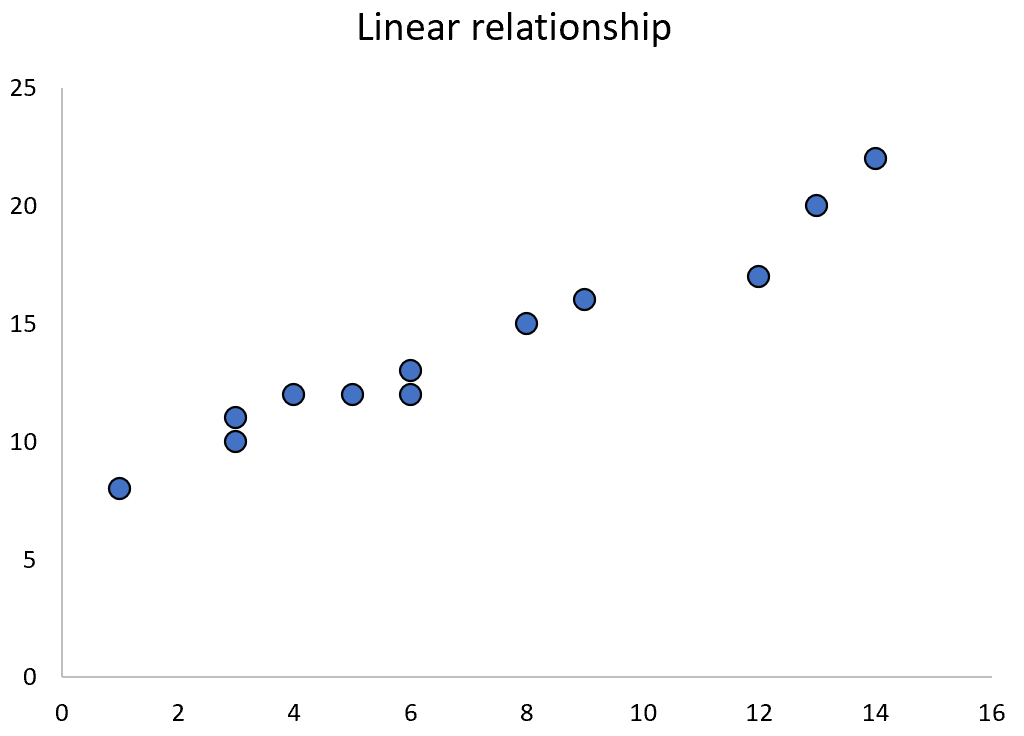
Однако, когда две переменные имеют квадратичную связь, мы можем вместо этого использовать квадратичную регрессию для количественной оценки их связи.
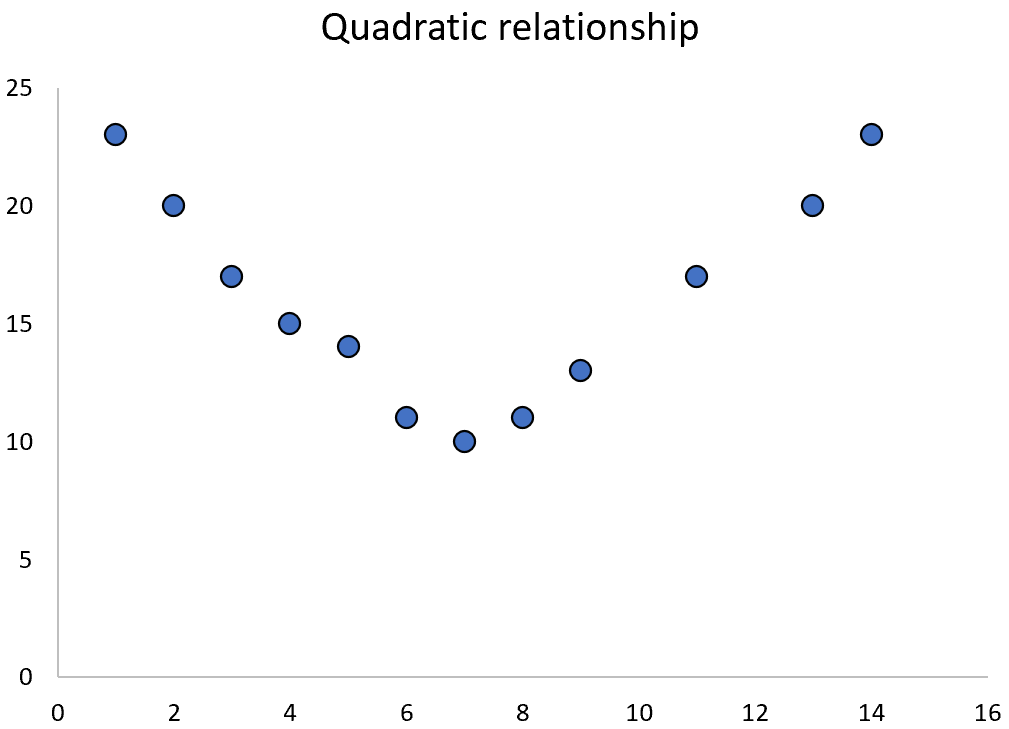
В этом руководстве объясняется, как выполнить квадратичную регрессию в R.
Пример: квадратичная регрессия в R
Предположим, нас интересует взаимосвязь между количеством отработанных часов и сообщаемым счастьем. У нас есть следующие данные о количестве отработанных часов в неделю и сообщаемом уровне счастья (по шкале от 0 до 100) для 11 разных людей:
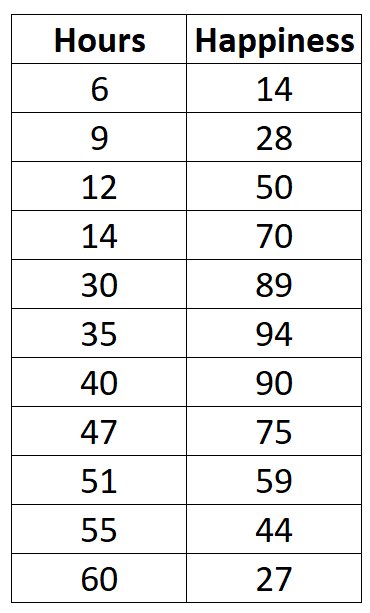
Используйте следующие шаги, чтобы подогнать модель квадратичной регрессии в R.
Шаг 1: Введите данные.
Сначала мы создадим фрейм данных, содержащий наши данные:
#create data
data <- data.frame(hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))
#view data
data
hours happiness
1 6 14
2 9 28
3 12 50
4 14 70
5 30 89
6 35 94
7 40 90
8 47 75
9 51 59
10 55 44
11 60 27
Шаг 2: Визуализируйте данные.
Далее мы создадим простую диаграмму рассеяния для визуализации данных.
#create scatterplot
plot(data$hours, data$happiness, pch=16)
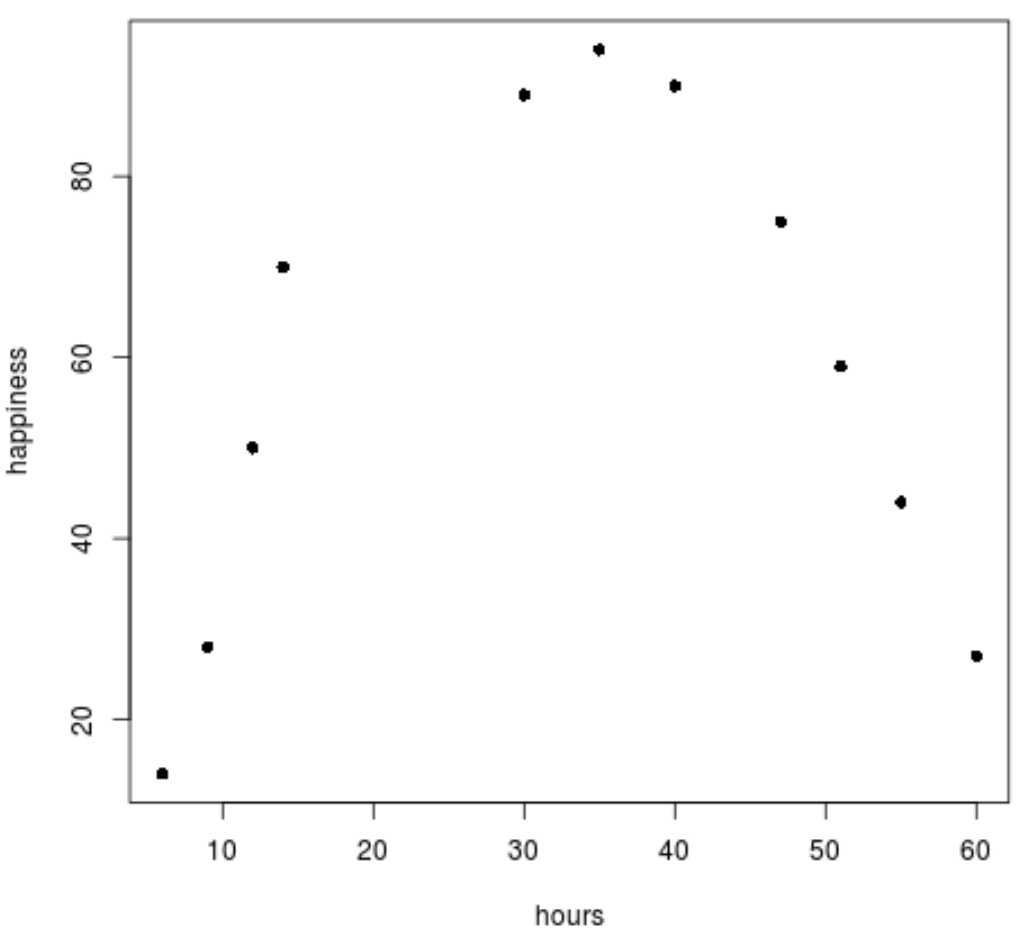
Мы можем ясно видеть, что данные не следуют линейному шаблону.
Шаг 3: Подберите простую модель линейной регрессии.
Далее мы подгоним простую модель линейной регрессии, чтобы увидеть, насколько хорошо она соответствует данным:
#fit linear model
linearModel <- lm(happiness ~ hours, data=data)
#view model summary
summary(linearModel)
Call:
lm(formula = happiness ~ hours)
Residuals:
Min 1Q Median 3Q Max
-39.34 -21.99 -2.03 23.50 35.11
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 48.4531 17.3288 2.796 0.0208 \*
hours 0.2981 0.4599 0.648 0.5331
---
Signif. codes: 0 '\*\*\*' 0.001 '\*\*' 0.01 '\*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 28.72 on 9 degrees of freedom
Multiple R-squared: 0.0446, Adjusted R-squared: -0.06156
F-statistic: 0.4201 on 1 and 9 DF, p-value: 0.5331
Общая дисперсия счастья, объясняемая моделью, составляет всего 4,46% , как показано значением множественного R-квадрата.
Шаг 4: Подберите модель квадратичной регрессии.
Далее мы подгоним модель квадратичной регрессии.
#create a new variable for hours 2
data$hours2 <- data$hours^2
#fit quadratic regression model
quadraticModel <- lm(happiness ~ hours + hours2, data=data)
#view model summary
summary(quadraticModel)
Call:
lm(formula = happiness ~ hours + hours2, data = data)
Residuals:
Min 1Q Median 3Q Max
-6.2484 -3.7429 -0.1812 1.1464 13.6678
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -18.25364 6.18507 -2.951 0.0184 \*
hours 6.74436 0.48551 13.891 6.98e-07 \*\*\*
hours2 -0.10120 0.00746 -13.565 8.38e-07 \*\*\*
---
Signif. codes: 0 '\*\*\*' 0.001 '\*\*' 0.01 '\*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 6.218 on 8 degrees of freedom
Multiple R-squared: 0.9602, Adjusted R-squared: 0.9502
F-statistic: 96.49 on 2 and 8 DF, p-value: 2.51e-06
Общая дисперсия счастья, объясняемая моделью, подскочила до 96,02% .
Мы можем использовать следующий код, чтобы визуализировать, насколько хорошо модель соответствует данным:
#create sequence of hour values
hourValues <- seq(0, 60, 0.1)
#create list of predicted happines levels using quadratic model
happinessPredict <- predict(quadraticModel,list(hours=hourValues, hours2=hourValues^2))
#create scatterplot of original data values
plot(data$hours, data$happiness, pch=16)
#add predicted lines based on quadratic regression model
lines(hourValues, happinessPredict, col='blue')
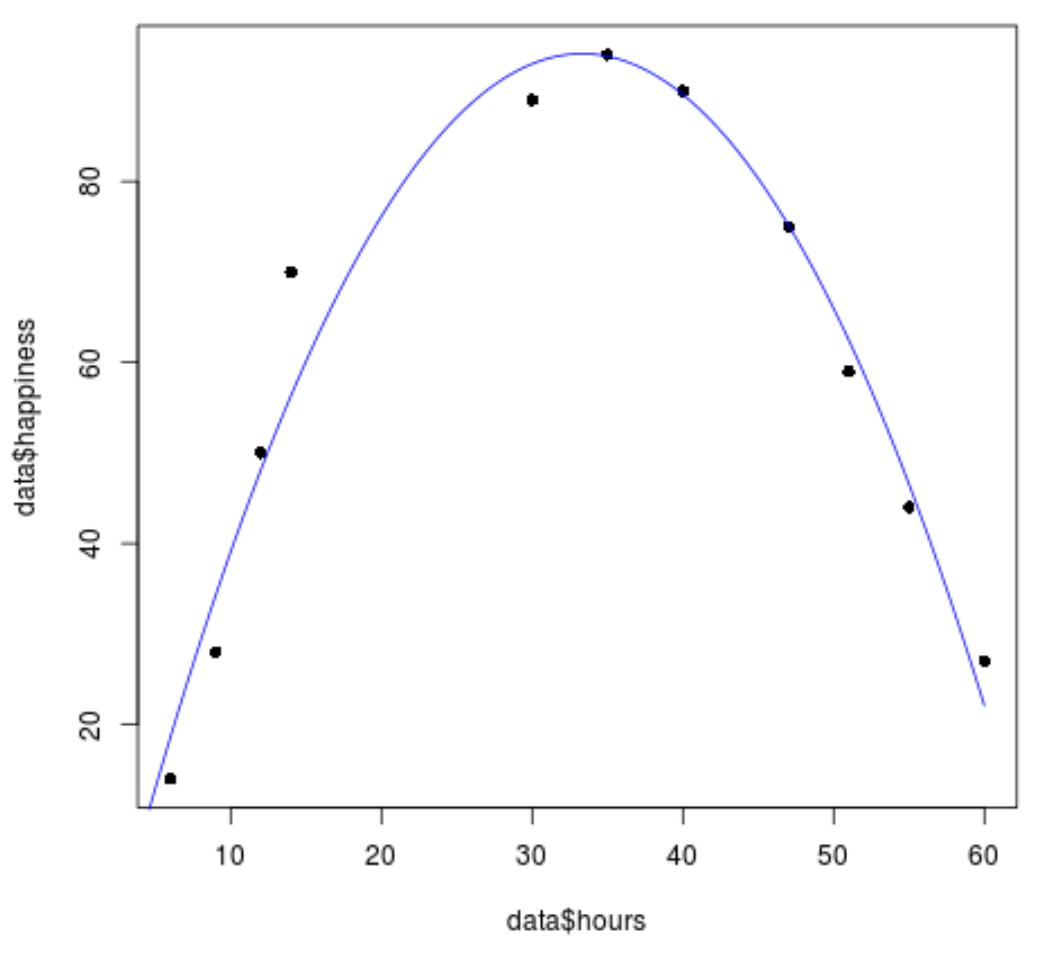
Мы видим, что линия квадратичной регрессии довольно хорошо соответствует значениям данных.
Шаг 5: Интерпретируйте модель квадратичной регрессии.
На предыдущем шаге мы видели, что результат модели квадратичной регрессии был следующим:
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -18.25364 6.18507 -2.951 0.0184 \*
hours 6.74436 0.48551 13.891 6.98e-07 \*\*\*
hours2 -0.10120 0.00746 -13.565 8.38e-07 \*\*\*
На основе коэффициентов, показанных здесь, подобранная квадратичная регрессия будет:
Счастье = -0,1012(час) 2 + 6,7444(час) - 18,2536
Мы можем использовать это уравнение, чтобы найти прогнозируемое счастье человека, учитывая количество часов, которые он работает в неделю.
Например, прогнозируется, что человек, который работает 60 часов в неделю, будет иметь уровень счастья 22,09 :
Счастье = -0,1012(60) 2 + 6,7444(60) – 18,2536 = 22,09
И наоборот, человек, который работает 30 часов в неделю, по прогнозам, будет иметь уровень счастья 92,99 :
Счастье = -0,1012(30) 2 + 6,7444(30) – 18,2536 = 92,99