Остаточная дисперсия (иногда называемая «необъяснимой дисперсией») относится к дисперсии в модели, которая не может быть объяснена переменными в модели.
Чем выше остаточная дисперсия модели, тем меньше модель способна объяснить изменение данных.
Остаточная дисперсия появляется на выходе двух разных статистических моделей:
1. Дисперсионный анализ: используется для сравнения средних значений трех или более независимых групп.
2. Регрессия: используется для количественной оценки взаимосвязи между одной или несколькими переменными-предикторами и переменной отклика .
В следующих примерах показано, как интерпретировать остаточную дисперсию в каждом из этих методов.
Остаточная дисперсия в моделях ANOVA
Всякий раз, когда мы подбираем модель ANOVA («дисперсионный анализ»), мы получаем таблицу ANOVA, которая выглядит следующим образом:
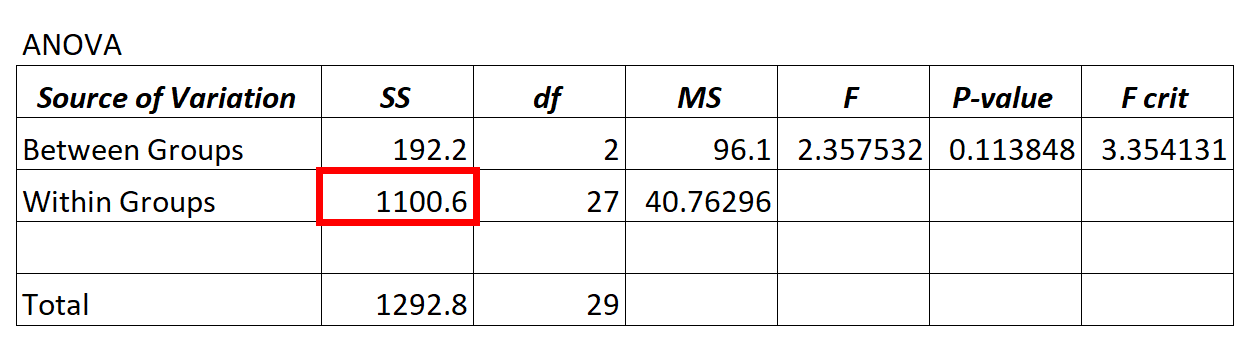
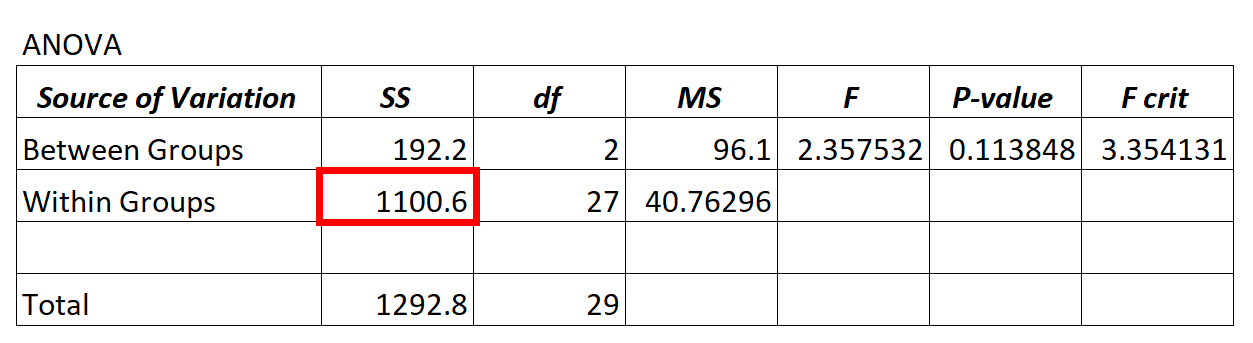
Значение остаточной дисперсии модели ANOVA можно найти в столбце SS («сумма квадратов») для варианта внутри групп .
Это значение также называется «сумма квадратов ошибок» и рассчитывается по следующей формуле:
Σ( Xij – Xj ) 2
куда:
- Σ : греческий символ, означающий «сумма».
- X ij : i -е наблюдение в группе j
- X j : среднее значение группы j
В приведенной выше модели ANOVA мы видим, что остаточная дисперсия составляет 1100,6.
Чтобы определить, является ли эта остаточная дисперсия «высокой», мы можем рассчитать среднюю сумму квадратов для внутри групп и среднюю сумму квадратов для между группами и найти соотношение между ними, что приводит к общему F-значению в таблице ANOVA.
- F = MS между / MS внутри
- F = 96,1/40,76296
- F = 2,357
Значение F в приведенной выше таблице ANOVA равно 2,357, а соответствующее значение p равно 0,113848. Поскольку это p-значение не меньше α = 0,05, у нас нет достаточных доказательств, чтобы отклонить нулевую гипотезу.
Это означает, что у нас нет достаточных доказательств, чтобы сказать, что средняя разница между группами, которые мы сравниваем, значительно отличается.
Это говорит нам о том, что остаточная дисперсия в модели ANOVA высока по сравнению с вариацией, которую модель фактически может объяснить.
Остаточная дисперсия в регрессионных моделях
В регрессионной модели остаточная дисперсия определяется как сумма квадратов разностей между прогнозируемыми точками данных и наблюдаемыми точками данных.
Он рассчитывается как:
Σ(ŷ i – y i ) 2
куда:
- Σ : греческий символ, означающий «сумма».
- ŷ i : прогнозируемые точки данных
- y i : наблюдаемые точки данных
Когда мы подбираем регрессионную модель, мы обычно получаем результат, который выглядит следующим образом:
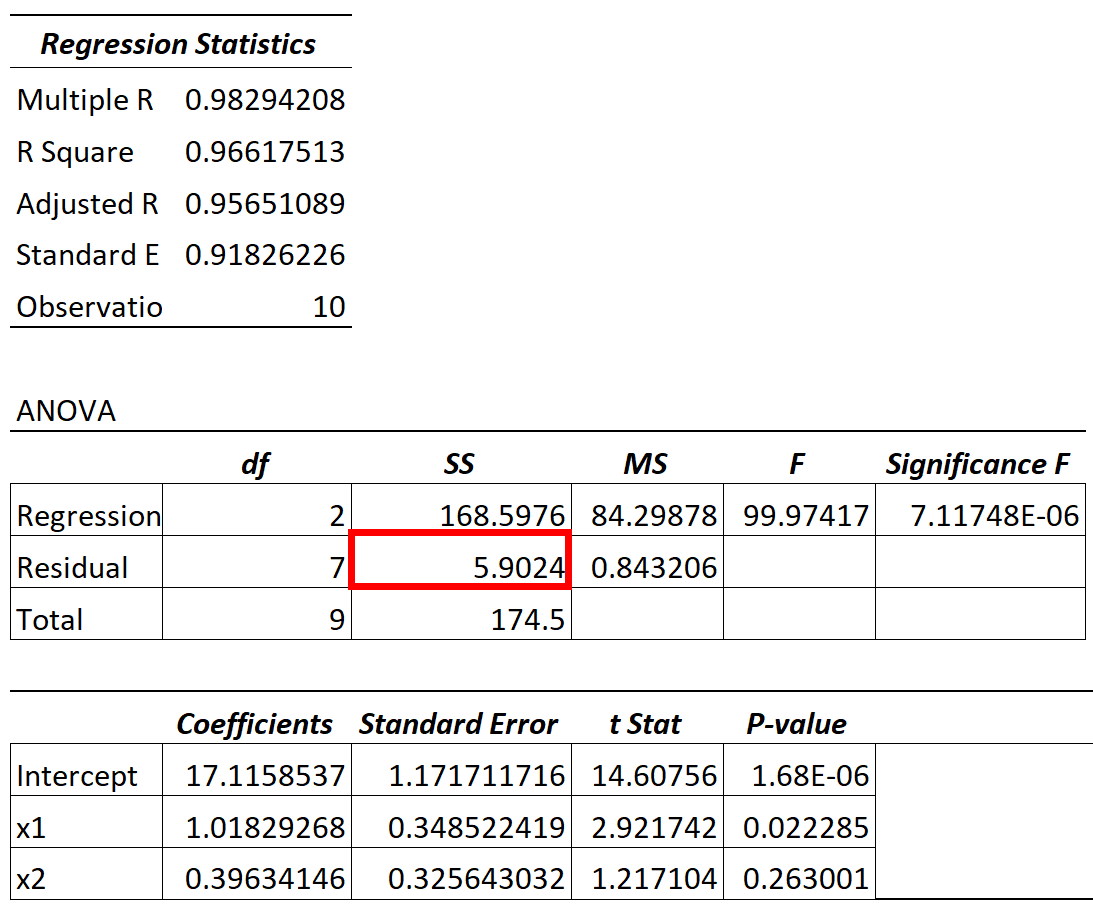
Значение остаточной дисперсии модели ANOVA можно найти в столбце SS («сумма квадратов») для остаточной вариации.
Отношение остаточной вариации к общей вариации в модели говорит нам о проценте вариации переменной отклика, которая не может быть объяснена предикторными переменными в модели.
Например, в приведенной выше таблице мы рассчитали бы этот процент как:
- Необъяснимая вариация = SS Residual / SS Total
- Необъяснимая вариация = 5,9024 / 174,5
- Необъяснимая вариация = 0,0338
Мы также можем рассчитать это значение, используя следующую формулу:
- Необъяснимая вариация = 1 – R 2
- Необъяснимая вариация = 1 – 0,96617
- Необъяснимая вариация = 0,0338
Значение R-квадрата для модели говорит нам о процентной вариации переменной отклика, которая может быть объяснена переменной-предиктором.
Таким образом, чем ниже необъяснимая вариация, тем лучше модель способна использовать переменные-предикторы для объяснения вариации переменной отклика.
Дополнительные ресурсы
Что такое хорошее значение R-квадрата?
Как рассчитать R-квадрат в Excel
Как рассчитать R-квадрат в R