Логистическая регрессия — это статистический метод, который мы используем для подбора модели регрессии, когда переменная отклика является бинарной. Чтобы оценить, насколько хорошо модель логистической регрессии соответствует набору данных, мы можем взглянуть на следующие две метрики:
- Чувствительность: вероятность того, что модель предсказывает положительный результат для наблюдения, когда результат действительно положительный.
- Специфичность: вероятность того, что модель предсказывает отрицательный результат для наблюдения, когда результат действительно отрицательный.
Один из простых способов визуализировать эти две метрики — создать кривую ROC , представляющую собой график, отображающий чувствительность и специфичность модели логистической регрессии.
В этом руководстве объясняется, как создать и интерпретировать кривую ROC в SPSS.
Пример: ROC-кривая в SPSS
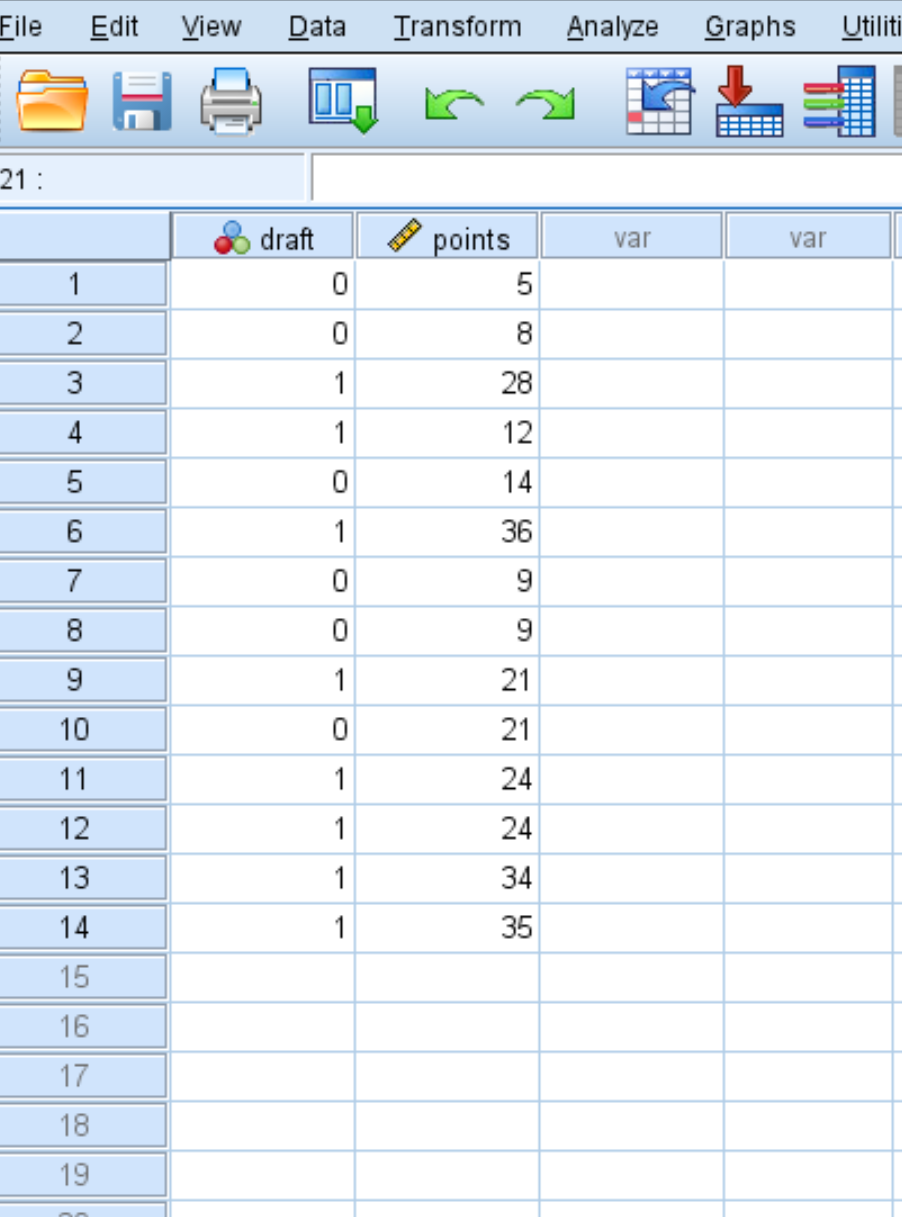
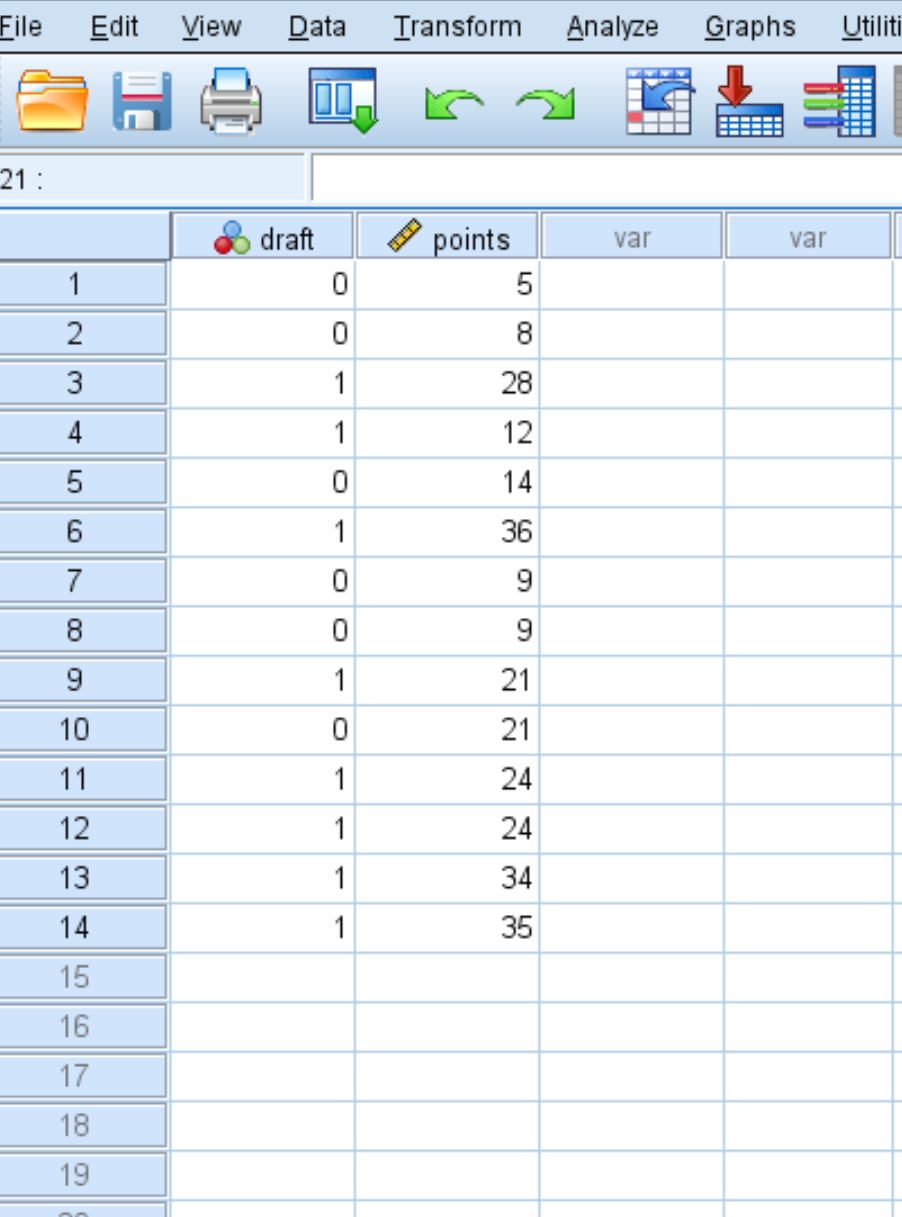
Предположим, у нас есть следующий набор данных, который показывает, попал ли баскетболист в НБА (0 = нет, 1 = да), а также его среднее количество очков за игру в колледже:
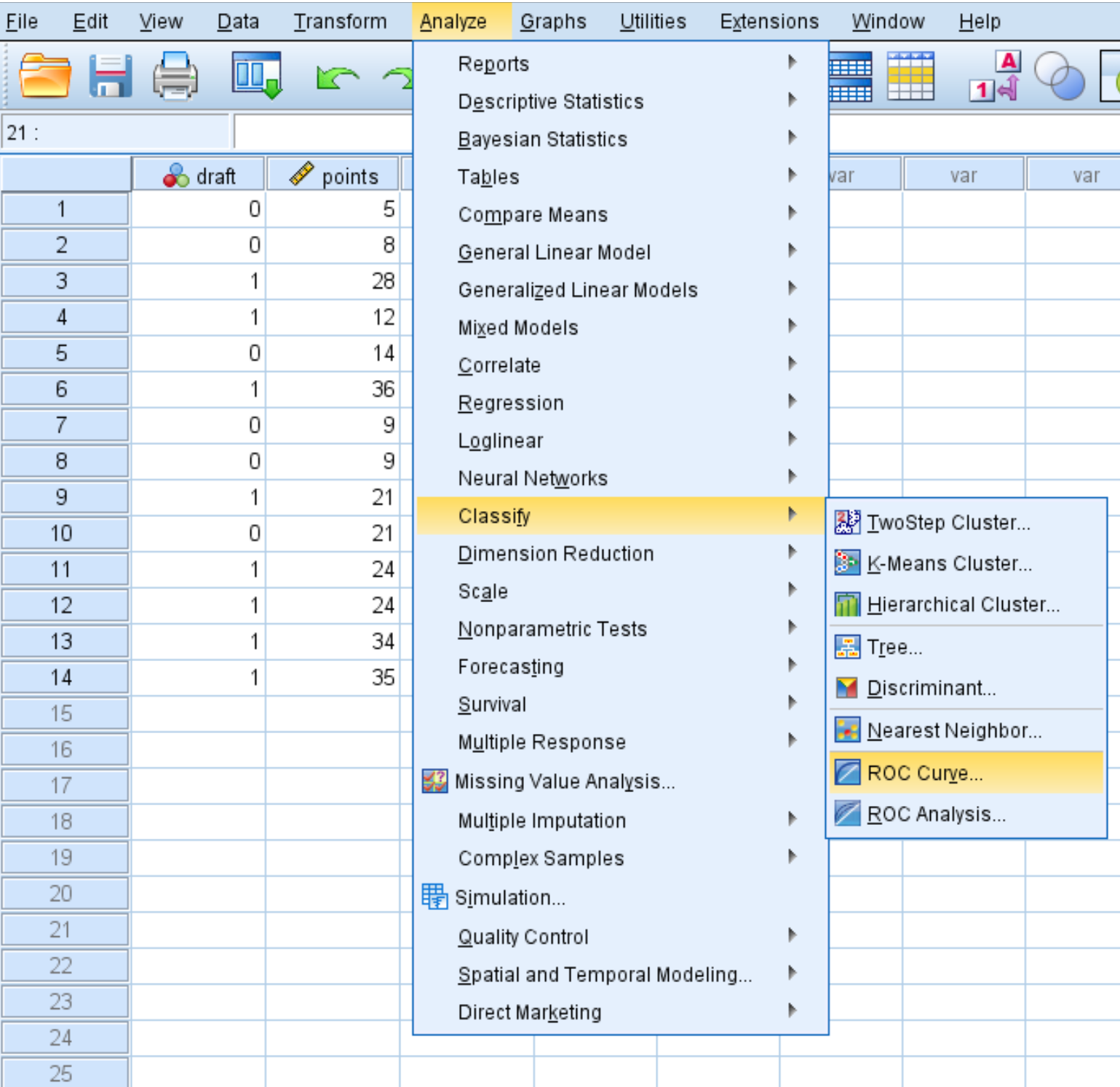
Чтобы создать кривую ROC для этого набора данных, перейдите на вкладку « Анализ », затем « Классификация », затем « Кривая ROC» :
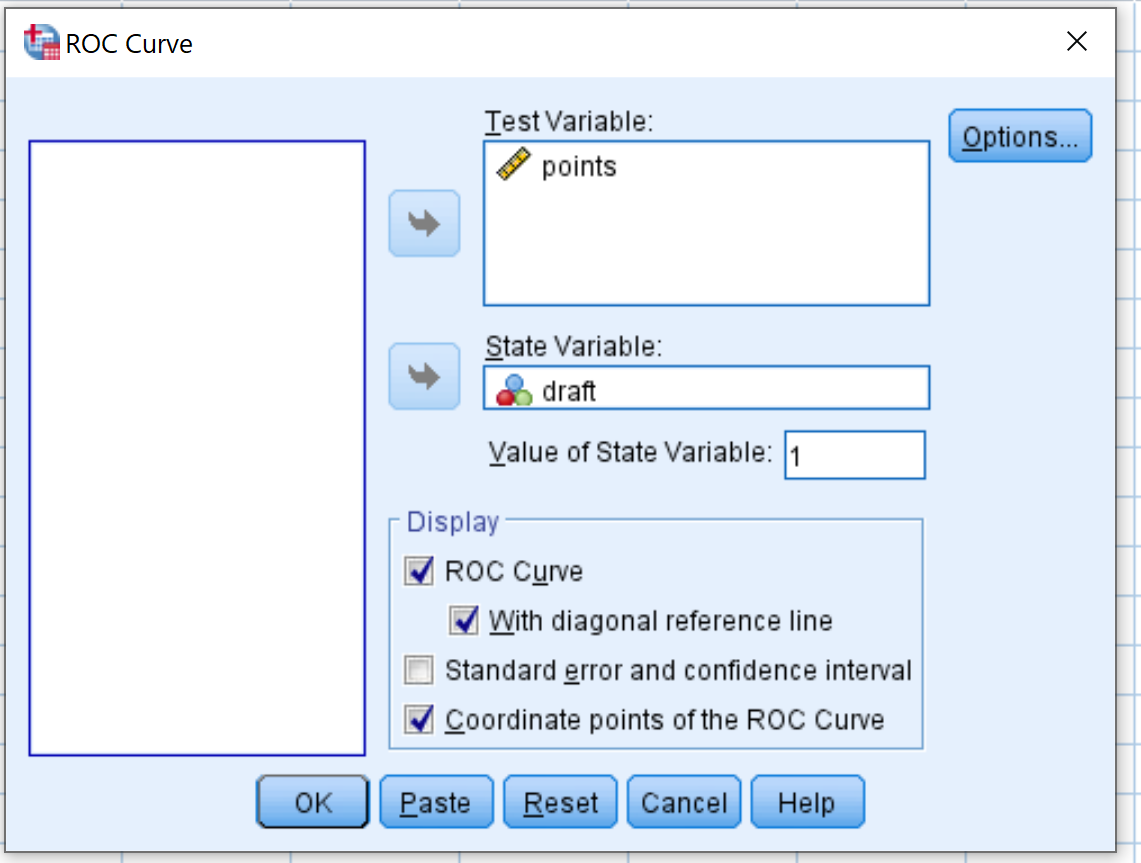
В появившемся новом окне перетащите переменную draft в поле с надписью State Variable. Определите значение переменной состояния равным 1.(Это значение указывает на то, что игрок выбран на драфте). Перетащите точки переменных в поле с надписью Test Variable.
Установите флажки рядом с С диагональной опорной линией и Координатными точками кривой ROC.Затем нажмите ОК .
Вот как интерпретировать вывод:
Резюме обработки дела:
В этой таблице отображается общее количество положительных и отрицательных случаев в наборе данных. В этом примере 8 игроков были выбраны на драфте (положительный результат) и 6 игроков не были выбраны на драфте (отрицательный результат):

ROC-кривая:
Кривая ROC (рабочая характеристика приемника) представляет собой график зависимости значений чувствительности от 1-специфичности при изменении значения точки отсечки от 0 до 1:
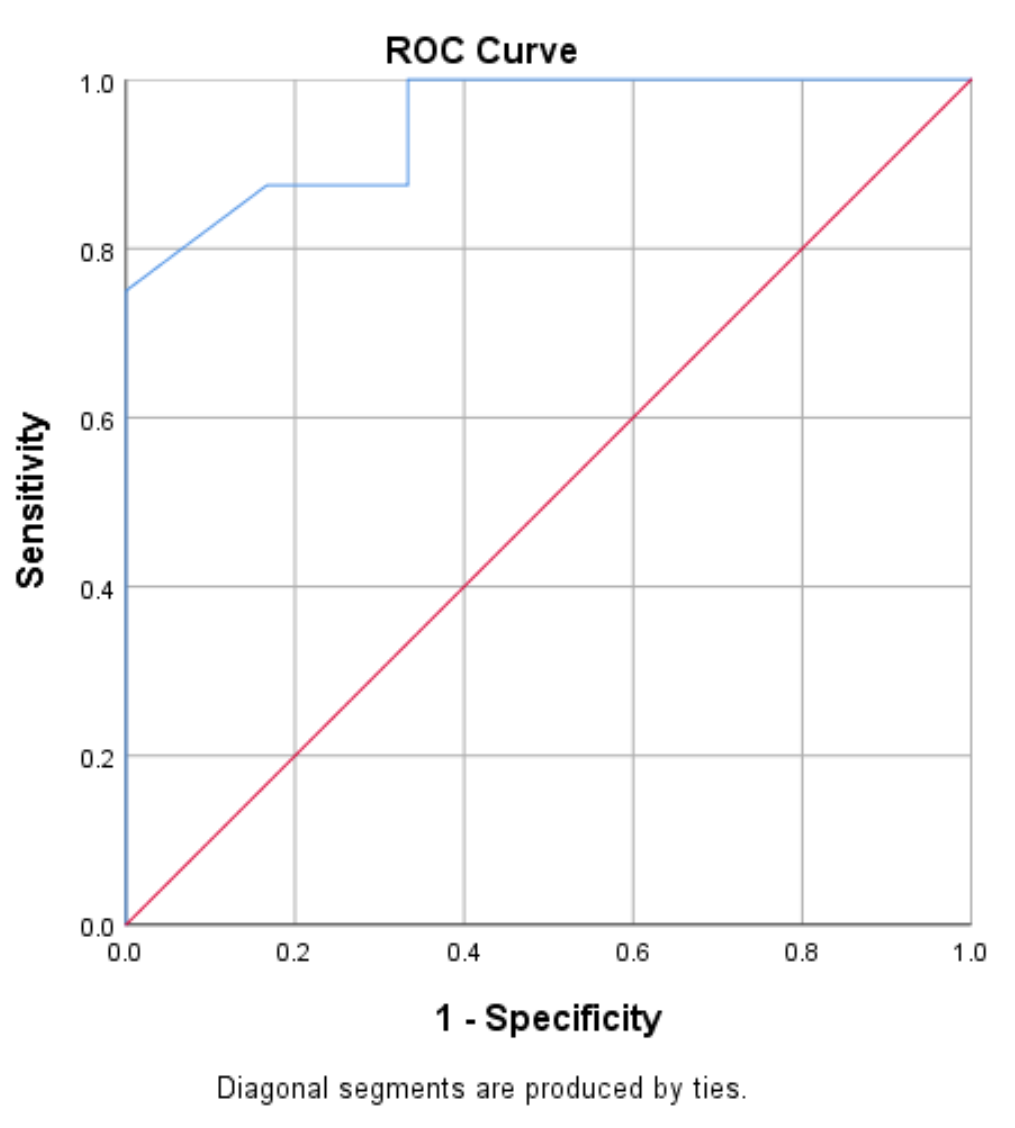
Модель с высокой чувствительностью и высокой специфичностью будет иметь кривую ROC, которая охватывает верхний левый угол графика. Модель с низкой чувствительностью и низкой специфичностью будет иметь кривую, близкую к диагональной линии под углом 45 градусов.
Мы видим, что кривая ROC (синяя линия) в этом примере охватывает верхний левый угол графика, что указывает на то, что модель хорошо предсказывает, будут ли игроки выбраны на драфте, основываясь на их среднем количестве очков за игру. .
Площадь под кривой:
Площадь под кривой дает нам представление о том, насколько хорошо модель способна различать положительные и отрицательные результаты. AUC может варьироваться от 0 до 1. Чем выше AUC, тем лучше модель правильно классифицирует результаты.
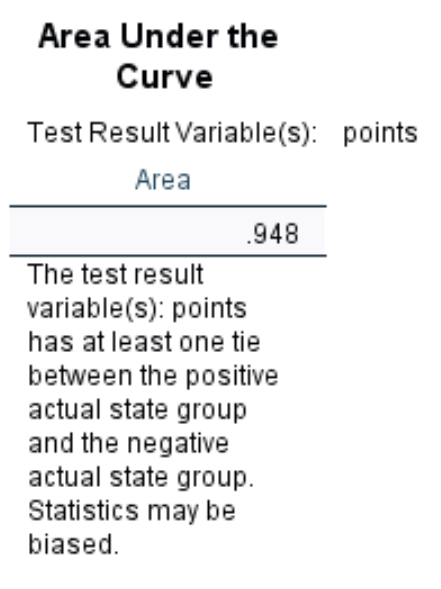
Мы видим, что AUC для этой конкретной модели логистической регрессии составляет 0,948 , что является чрезвычайно высоким показателем. Это указывает на то, что модель хорошо предсказывает, будет ли игрок выбран на драфте.
Координаты кривой:
Эта последняя таблица отображает чувствительность и 1 – специфичность ROC-кривой для различных точек отсечки.
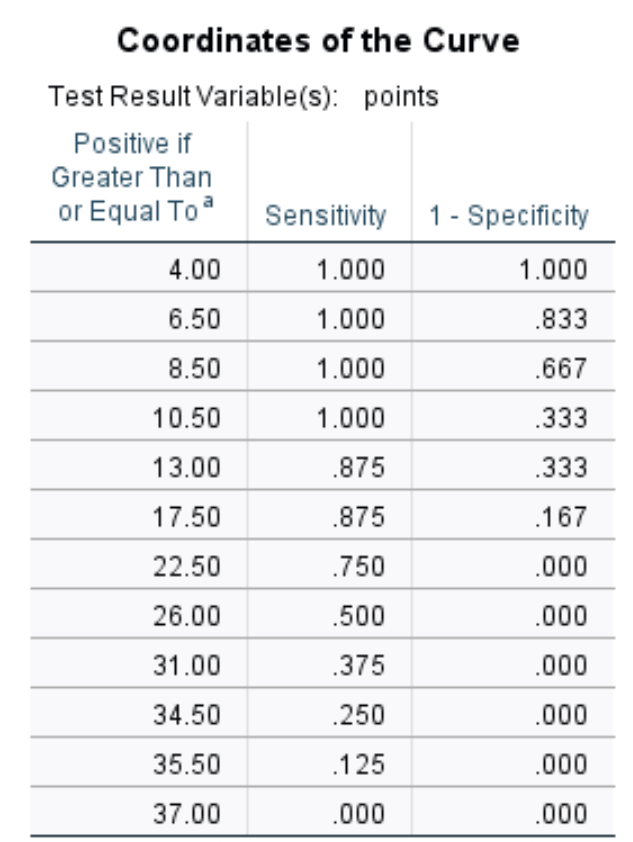
Например:
Если мы допустим, что точка отсечения равна 8,50 , это означает, что мы прогнозируем, что любой игрок, набравший менее 8,50 очков за игру, не будет выбран на драфте, а любой игрок, набравший более 8,50 очков за игру, будет выбран.
Если использовать это как точку отсечки, наша чувствительность будет равна 100 % (поскольку каждый игрок, набравший менее 8,50 очков за игру, действительно не был выбран на драфте), а наша 1-специфичность составит 66,7 % (поскольку 8 из 12 игроков, набравших на драфте действительно было больше 8,50 очков за игру).
Приведенная выше таблица позволяет нам увидеть чувствительность и 1-специфичность для каждой потенциальной пороговой точки.