В статистике стандартное отклонение используется для измерения разброса значений в выборке.
Мы можем использовать следующую формулу для расчета стандартного отклонения данной выборки:
√ Σ(x i – x бар ) 2 / (n-1)
куда:
- Σ: символ, означающий «сумма».
- x i : i -е значение в выборке
- x bar : среднее значение выборки
- n: размер выборки
Чем выше значение стандартного отклонения, тем более разбросаны значения в выборке .
Чем ниже значение стандартного отклонения, тем более плотно упакованы значения.
Если стандартное отклонение выборки равно нулю, это означает, что все значения в выборке абсолютно одинаковы.
Другими словами, существует нулевой разброс значений.
В следующем примере показано, как интерпретировать стандартное отклонение нуля на практике.
Пример: как интерпретировать стандартное отклонение нуля
Предположим, мы собираем простую случайную выборку из 10 ящериц и измеряем их длину (в дюймах):
Длины : 7, 7, 7, 7, 7, 7, 7, 7, 7, 7
Средняя длина ящериц в выборке составляет 7 дюймов.
Зная это, мы можем рассчитать стандартное отклонение выборки (s) для этого набора данных:
- s = √ Σ(x i – x бар ) 2 / (n-1)
- s = √ ((7 – 7) 2 + (7 – 7) 2 + (7 – 7) 2 + … + (7 – 7) 2 / (10-1)
- s = √ 0 2 + 0 2 + 0 2 + … + 0 2 / 9
- с = 0
Стандартное отклонение выборки оказывается равным 0 .
Поскольку каждая ящерица имеет одинаковую длину, разброс значений в наборе данных точно равен нулю.
Станет ли стандартное отклонение когда-либо равным нулю в реальном мире?
Вполне возможно, что реальный набор данных может иметь стандартное отклонение, равное нулю, но это случается редко.
Наиболее вероятный сценарий, в котором вы можете столкнуться со стандартным отклонением, равным нулю, — это сбор небольших выборок для редких событий.
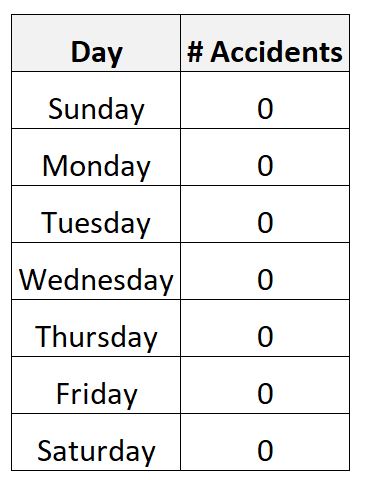
Например, предположим, что вы собираете данные о количестве дорожно-транспортных происшествий за недельный интервал в определенном городе.
Вполне возможно, что вы могли бы собрать следующие данные:

В этом сценарии среднее количество ежедневных аварий будет равно нулю, и стандартное отклонение также будет равно нулю.
Или, возможно, вы собираете следующие данные о количестве ежемесячных продаж какого-либо дорогого продукта для какой-либо компании в течение 6-месячного периода времени:

Поскольку продукт очень дорогой, так уж получилось, что компания продает только два продукта в месяц.
В этом сценарии среднее количество ежемесячно продаваемых продуктов равно двум, а стандартное отклонение ежемесячно проданных продуктов равно нулю.
Всякий раз, когда вы сталкиваетесь со стандартным отклонением, равным нулю, в реальном наборе данных, просто знайте, что это означает, что все значения в наборе данных абсолютно одинаковы.
Дополнительные ресурсы
Следующие руководства предоставляют дополнительную информацию о стандартном отклонении в статистике:
Почему важно стандартное отклонение?
Стандартное отклонение и стандартная ошибка: в чем разница?
Стандартное отклонение и межквартильный диапазон: в чем разница?