В статистике нам часто интересно понять, как распространяется набор данных. В частности, есть четыре вещи, которые полезно знать о дистрибутиве:
1 . Форма
- Распределение симметрично или смещено в одну сторону?
- Является ли распределение одномодальным (один пик) илибимодальным (два пика)?
2. Выбросы
- Присутствуют ли какие-либо выбросы в распределении?
3. Центр
- Что такое среднее значение, медиана и способ распределения?
4. Распространение
- Что такое размах, межквартильный размах, стандартное отклонение и дисперсия распределения?
SOCS — полезная аббревиатура, которую мы можем использовать, чтобы запомнить эти четыре вещи. Это означает «форма, выбросы, центр, распространение».
Давайте рассмотрим простой пример того, как использовать SOCS для описания дистрибутива.
Пример: как использовать SOCS для описания дистрибутива
Предположим, у нас есть следующий набор данных, который показывает высоту выборки из 20 разных растений.

Вот как мы можем использовать SOCS для описания этого распределения значений данных.
Форма
Во-первых, мы хотим описать форму распределения.
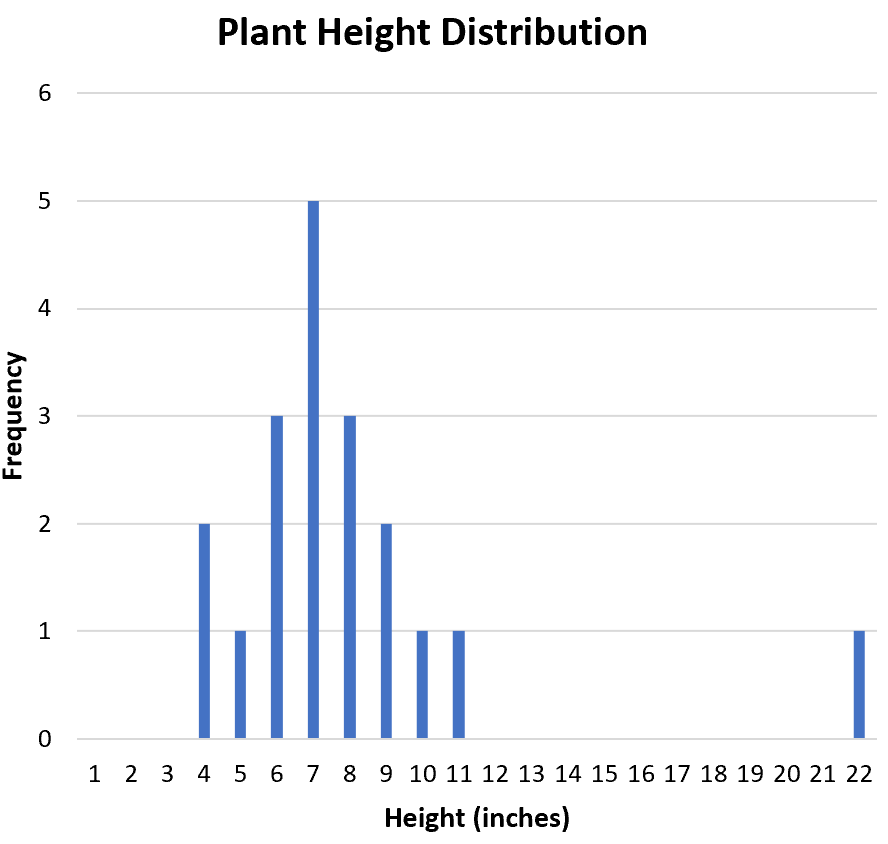
Одним из полезных способов визуализации формы распределения является создание гистограммы, которая отображает частоты каждого значения в наборе данных:

Распределение симметрично или смещено в одну сторону? Из гистограммы видно, что распределение примерно симметрично. То есть значения не перекошены в ту или иную сторону.
Является ли распределение одномодальным (один пик) или бимодальным (два пика)? Распространение унимодальное. Он имеет один пик при значении «7».
Выбросы
Затем мы хотим определить, есть ли какие-либо выбросы в наборе данных. Из гистограммы мы можем визуально проверить распределение и увидеть, что 22 потенциально является выбросом:
Одним из распространенных способов формального определения выброса является любое значение, которое в 1,5 раза превышает межквартильный диапазон выше третьего квартиля или ниже первого квартиля.
Используя калькулятор межквартильного диапазона, мы можем ввести 20 необработанных значений данных и обнаружить, что третий квартиль равен 9 , межквартильный диапазон равен 3 , и, таким образом, любое значение выше 9 + (1,5 * 3) = 13,5 является выбросом по определению.
Поскольку 22 больше 13,5, мы можем объявить 22 выбросом.
Центр
Далее мы хотим описать, где находится центр распределения. Три общих показателя центральной тенденции , которые мы можем использовать, — это среднее значение, медиана и мода.
Среднее: это среднее значение в распределении. Мы находим это путем сложения всех отдельных значений, а затем деления на общее количество значений:
Среднее = (8+4+6+7+7+6+7+8+6+11+8+22+10+9+9+7+5+7+6+4) / 20 = 7,85
Медиана: это «среднее» значение в распределении. Мы находим это, упорядочивая все значения от наименьшего к наибольшему, а затем определяя среднее значение. Получается 7 .
4, 4, 5, 6, 6, 6, 6, 7, 7, 7 , 7 , 7, 8, 8, 8, 9, 9, 10, 11, 22
Режим: это значение, которое встречается чаще всего. Получается 7 .
Распространять
Далее мы хотим описать, насколько разбросаны значения в распределении. Четыре общих показателя дисперсии , которые мы можем использовать, — это размах, межкварильный размах, стандартное отклонение и дисперсия.
Диапазон: это разница между наибольшим и наименьшим значением в наборе данных. Получается 22 – 4 = 18 .
Межквартильный диапазон: измеряет ширину средних 50% значений данных. Введя 20 необработанных значений данных в калькулятор межквартильного диапазона , мы видим, что это равно 3 .
Стандартное отклонение: это мера того, насколько разбросаны значения данных в среднем. Введя 20 необработанных значений данных в калькулятор дисперсии и стандартного отклонения, мы видим, что стандартное отклонение равно 3,69 .
Дисперсия: это просто стандартное отклонение, возведенное в квадрат. Это равно 3,69 2 = 13,63 .
Вывод
Используя SOCS в качестве ориентира, мы смогли описать распределение высоты растений следующим образом:
- Распределение было унимодальным и симметричным, то есть имело только один пик и не было смещено в ту или иную сторону.
- В распределении был один выброс: 22.
- Распределение имело среднее значение 7,85, медиану 7 и моду 7.
- Распределение имело диапазон 18, межквартильный диапазон 3, стандартное отклонение 3,69 и дисперсию 13,63.
Обратите внимание, что мы можем использовать SOCS для описания любого распределения, что является полезным способом получить хорошее представление о форме распределения, есть ли в нем какие-либо выбросы, где примерно расположен центр и как распределены значения данных. находятся.


