В статистике однофакторный дисперсионный анализ используется для сравнения средних значений трех или более независимых групп, чтобы определить, существует ли статистически значимая разница между соответствующими средними значениями генеральной совокупности.
Всякий раз, когда вы выполняете однофакторный дисперсионный анализ, вы всегда будете вычислять три значения суммы квадратов:
1. Регрессия суммы квадратов (SSR)
- Это сумма квадратов разностей между средним значением каждой группы и общим средним значением .
2. Ошибка суммы квадратов (SSE)
- Это сумма квадратов разностей между каждым отдельным наблюдением и групповым средним значением этого наблюдения.
3. Общая сумма квадратов (SST)
- Это сумма квадратов разностей между каждым отдельным наблюдением и средним значением.
Каждое из этих трех значений помещается в итоговую таблицу ANOVA, которую мы используем, чтобы определить, существует ли статистически значимая разница между средними группами.
В следующем примере показано, как на практике рассчитать каждое из этих значений суммы квадратов для однофакторного дисперсионного анализа.
Пример: как рассчитать сумму квадратов в ANOVA
Предположим, мы хотим знать, приводят ли три разные программы подготовки к экзаменам к разным средним баллам на определенном экзамене. Чтобы проверить это, мы набираем 30 студентов для участия в исследовании и разделяем их на три группы.
Студенты в каждой группе случайным образом назначаются для использования одной из трех программ подготовки к экзамену в течение следующих трех недель для подготовки к экзамену. По истечении трех недель все студенты сдают один и тот же экзамен.
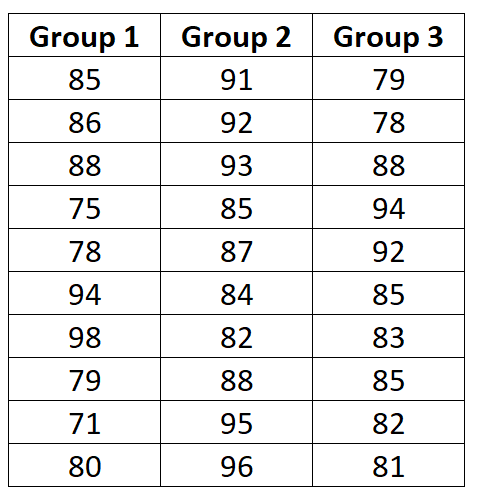
Ниже представлены результаты экзаменов для каждой группы:
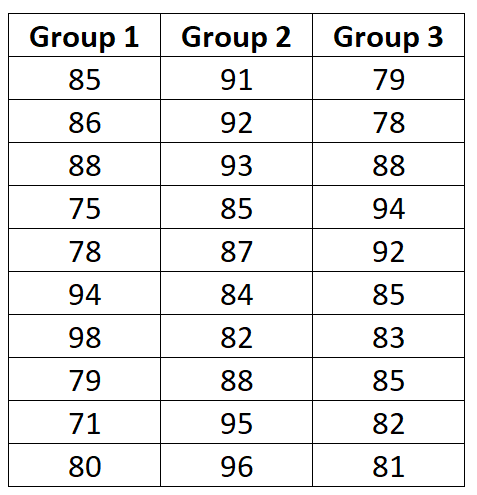
Следующие шаги показывают, как рассчитать сумму квадратов значений для этого однофакторного дисперсионного анализа.
Шаг 1: Рассчитайте групповые средние и общее среднее.
Во-первых, мы рассчитаем среднее значение для всех трех групп вместе с общим (или «общим») средним значением:
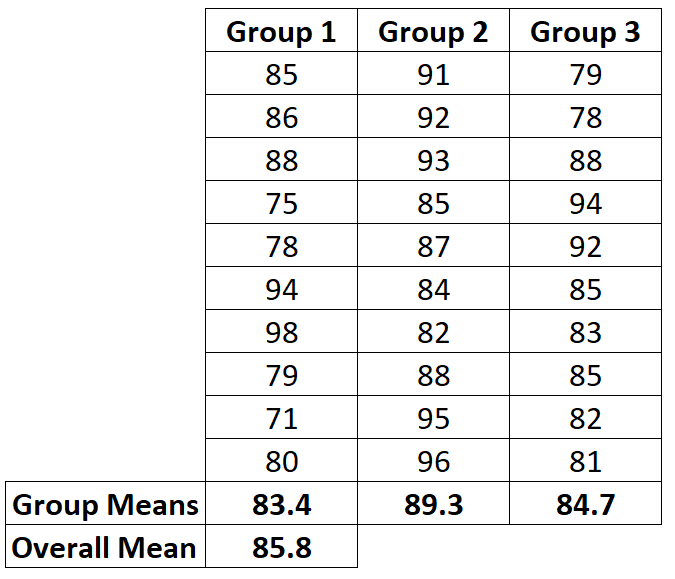
Шаг 2: Рассчитайте SSR.
Далее мы рассчитаем сумму квадратов регрессии (SSR) по следующей формуле:
nΣ(X j – X ..) 2
куда:
- n : размер выборки группы j
- Σ : греческий символ, означающий «сумма».
- X j : среднее значение группы j
- X .. : общее среднее значение
В нашем примере мы вычисляем, что SSR = 10(83,4-85,8) 2 + 10(89,3-85,8) 2 + 10(84,7-85,8) 2 = 192,2
Шаг 3: Рассчитайте SSE.
Далее мы рассчитаем ошибку суммы квадратов (SSE) по следующей формуле:
Σ( Xij – Xj ) 2
куда:
- Σ : греческий символ, означающий «сумма».
- X ij : i -е наблюдение в группе j
- X j : среднее значение группы j
В нашем примере мы вычисляем SSE следующим образом:
1 группа: (85-83,4) 2 + (86-83,4) 2 +(88-83,4) 2 +(75-83,4) 2 +(78-83,4) 2 +(94-83,4) 2 +(98-83,4) 2 +(79-83,4) 2 +(71-83,4) 2 +(80-83,4) 2 = 640,4
2 группа: (91-89,3) 2 + (92-89,3) 2 +(93-89,3) 2 +(85-89,3) 2 +(87-89,3) 2 +(84-89,3) 2 +(82-89,3) 2 +(88-89,3) 2 +(95-89,3) 2 +(96-89,3) 2 = 208,1
3 группа: (79-84,7) 2 + (78-84,7) 2 +(88-84,7) 2 +(94-84,7) 2 +(92-84,7) 2 +(85-84,7) 2 +(83-84,7) 2 +(85-84,7) 2 +(82-84,7) 2 +(81-84,7) 2 = 252,1
ССЭ: 640,4 + 208,1 + 252,1 = 1100,6
Шаг 4: Рассчитайте SST.
Далее мы рассчитаем общую сумму квадратов (SST) по следующей формуле:
SST = SSR + SSE
В нашем примере SST = 192,2 + 1100,6 = 1292,8.
Как только мы рассчитали значения для SSR, SSE и SST, каждое из этих значений в конечном итоге будет помещено в таблицу ANOVA:
| Источник | Сумма квадратов (СС) | дф | Средние квадраты (MS) | F-значение | р-значение | | --- | --- | --- | --- | --- | --- | | Регрессия | 192,2 | 2 | 96,1 | 2,358 | 0,1138 | | Ошибка | 1100,6 | 27 | 40,8 | | | | Общий | 1292,8 | 29 | | | |
Вот как мы рассчитали различные числа в таблице:
- регрессия df: k-1 = 3-1 = 2
- ошибка df: nk = 30-3 = 27
- df всего: n-1 = 30-1 = 29
- Лечение MS: лечение SST / df = 192,2 / 2 = 96,1
- Ошибка MS: ошибка SSE/df = 1100,6/27 = 40,8
- Значение F: обработка МС/ошибка МС = 96,1/40,8 = 2,358.
- p-значение : p-значение, соответствующее значению F.
Примечание: n = общее количество наблюдений, k = количество групп.
Ознакомьтесь с этим руководством , чтобы узнать, как интерпретировать F-значение и p-значение в таблице ANOVA.