Многие статистические тесты предполагают , что наборы данных обычно распределяются.
Есть четыре распространенных способа проверить это предположение в R:
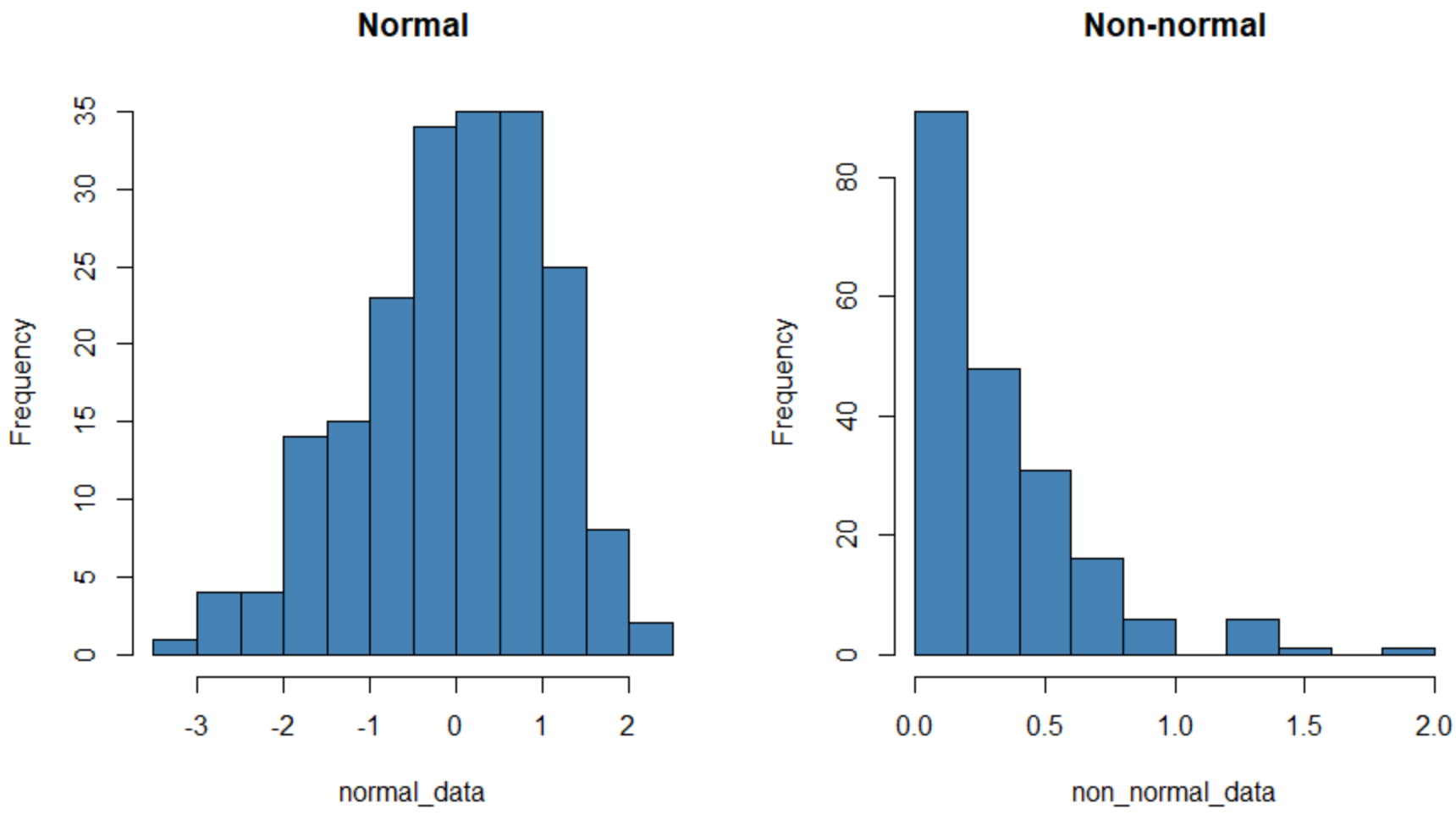
1. (Визуальный метод) Создайте гистограмму.
- Если гистограмма имеет форму колокола, то считается, что данные распределены нормально.
2. (Визуальный метод) Создайте график QQ.
- Если точки на графике примерно совпадают с прямой диагональной линией, предполагается, что данные распределены нормально.
3. (Формальный статистический тест) Выполните тест Шапиро-Уилка.
- Если p-значение теста больше, чем α = 0,05, то предполагается, что данные распределены нормально.
4. (Формальный статистический тест) Выполните тест Колмогорова-Смирнова.
- Если p-значение теста больше, чем α = 0,05, то предполагается, что данные распределены нормально.
В следующих примерах показано, как использовать каждый из этих методов на практике.
Способ 1: создание гистограммы
В следующем коде показано, как создать гистограмму для нормально распределенного и ненормально распределенного набора данных в R:
#make this example reproducible
set. seed (0)
#create data that follows a normal distribution
normal_data <- rnorm(200)
#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)
#define plotting region
par(mfrow=c(1,2))
#create histogram for both datasets
hist(normal_data, col='steelblue', main='Normal')
hist(non_normal_data, col='steelblue', main='Non-normal')

На гистограмме слева показан набор данных с нормальным распределением (примерно «колокольчик»), а на гистограмме справа представлен набор данных с ненормальным распределением.
Способ 2: создать график QQ
В следующем коде показано, как создать график QQ для нормально распределенного и ненормально распределенного набора данных в R:
#make this example reproducible
set. seed (0)
#create data that follows a normal distribution
normal_data <- rnorm(200)
#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)
#define plotting region
par(mfrow=c(1,2))
#create Q-Q plot for both datasets
qqnorm(normal_data, main='Normal')
qqline(normal_data)
qqnorm(non_normal_data, main='Non-normal')
qqline(non_normal_data)

На графике QQ слева представлен набор данных с нормальным распределением (точки падают на прямую диагональную линию), а на графике QQ справа представлен набор данных с ненормальным распределением.
Метод 3: выполнить тест Шапиро-Уилка
В следующем коде показано, как выполнить тест Шапиро-Уилка для нормально распределенного и ненормально распределенного набора данных в R:
#make this example reproducible
set. seed (0)
#create data that follows a normal distribution
normal_data <- rnorm(200)
#perform shapiro-wilk test
shapiro. test (normal_data)
Shapiro-Wilk normality test
data: normal_data
W = 0.99248, p-value = 0.3952
#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)
#perform shapiro-wilk test
shapiro. test (non_normal_data)
Shapiro-Wilk normality test
data: non_normal_data
W = 0.84153, p-value = 1.698e-13
Значение p первого теста не менее 0,05, что указывает на нормальное распределение данных.
Значение p второго теста меньше 0,05, что указывает на то, что данные не распределены нормально.
Метод 4: выполнить тест Колмогорова-Смирнова
В следующем коде показано, как выполнить тест Колмогорова-Смирнова для нормально распределенного и ненормально распределенного набора данных в R:
#make this example reproducible
set. seed (0)
#create data that follows a normal distribution
normal_data <- rnorm(200)
#perform kolmogorov-smirnov test
ks. test (normal_data, 'pnorm')
One-sample Kolmogorov-Smirnov test
data: normal_data
D = 0.073535, p-value = 0.2296
alternative hypothesis: two-sided
#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)
#perform kolmogorov-smirnov test
ks. test (non_normal_data, 'pnorm')
One-sample Kolmogorov-Smirnov test
data: non_normal_data
D = 0.50115, p-value < 2.2e-16
alternative hypothesis: two-sided
Значение p первого теста не менее 0,05, что указывает на нормальное распределение данных.
Значение p второго теста меньше 0,05, что указывает на то, что данные не распределены нормально.
Как обращаться с ненормальными данными
Если данный набор данных не имеет нормального распределения, мы часто можем выполнить одно из следующих преобразований, чтобы сделать его более нормально распределенным:
1. Преобразование журнала: преобразование значений из x в log(x) .
2. Преобразование квадратного корня: преобразование значений из x в √ x .
3. Преобразование кубического корня: преобразование значений от x до x 1/3 .
Выполняя эти преобразования, набор данных обычно становится более нормально распределенным.
Прочтите этот учебник , чтобы узнать, как выполнить эти преобразования в R.
Дополнительные ресурсы
Как создавать гистограммы в R
Как создать и интерпретировать график QQ в R
Как выполнить тест Шапиро-Уилка в R
Как выполнить тест Колмогорова-Смирнова в R