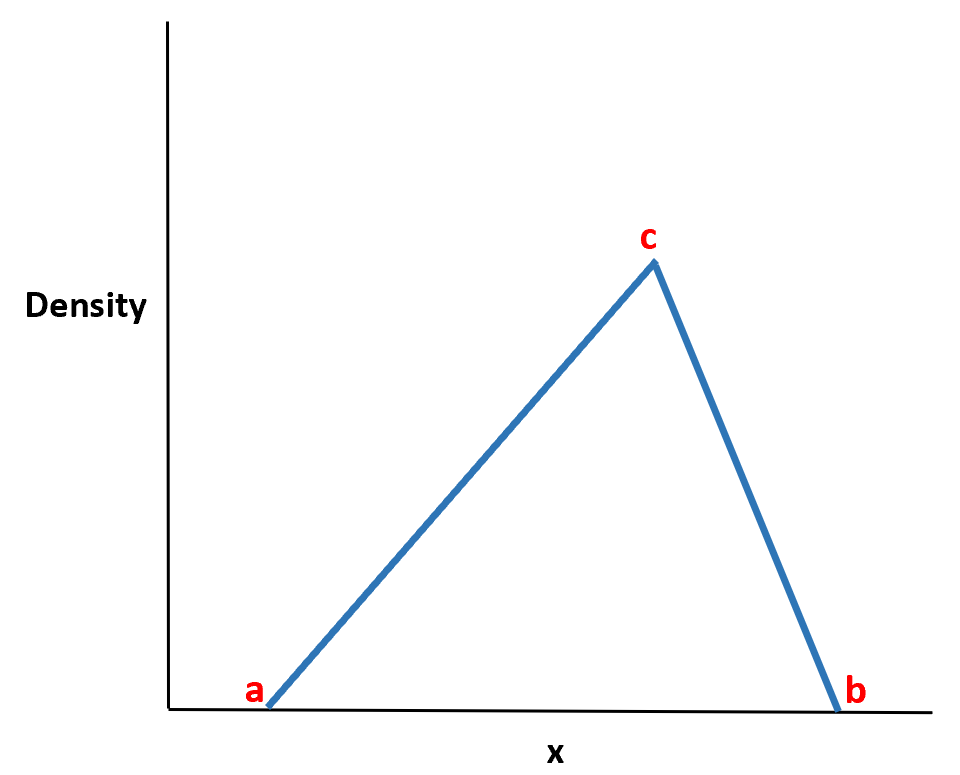
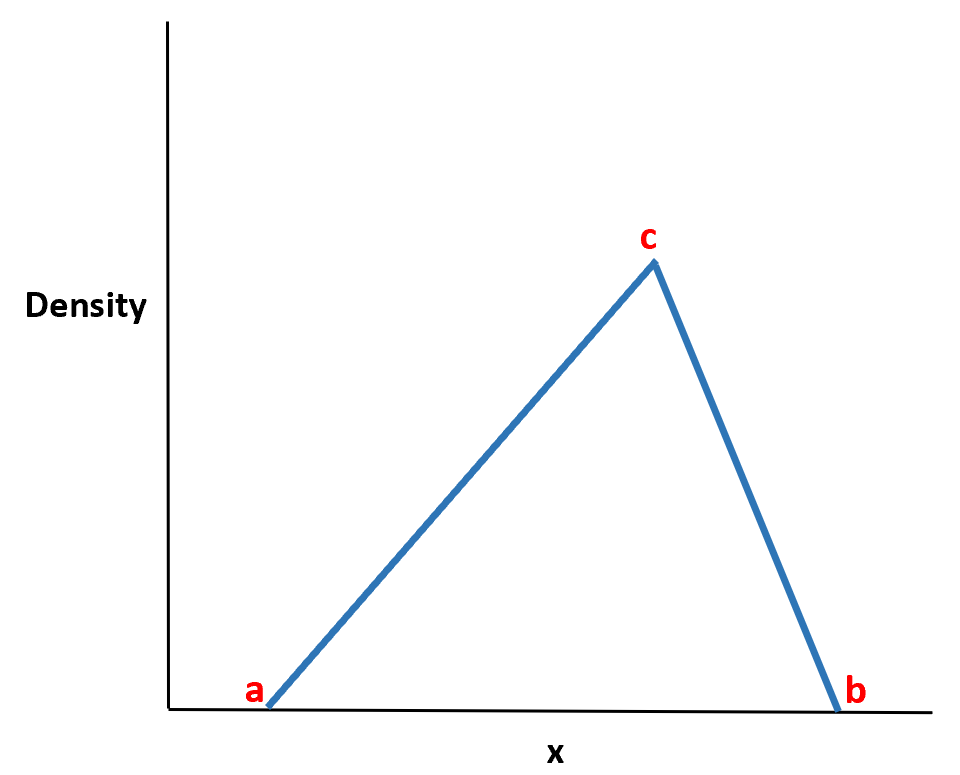
Треугольное распределение представляет собой непрерывное распределение вероятностей с функцией плотности вероятности в форме треугольника.
Он определяется тремя значениями:
- Минимальное значение а
- Максимальное значение б
- Пиковое значение с
Чтобы вычислить вероятности для треугольного распределения в R, мы можем использовать функцию ptri( ) из пакета EnvStats , которая использует следующий синтаксис:
ptri(q, мин. = 0, макс. = 1, мода = 1/2)
куда:
- q : Квантиль интереса
- min : минимальное значение распределения
- max : максимальное значение распределения
- mode : Пиковое значение распределения
В следующих примерах показано, как использовать эту функцию на практике в R.
Пример 1: Расчет вероятности меньше некоторого значения
Предположим, ресторан оценивает, что их общий объем продаж на предстоящей неделе составит минимум 10 000 долларов, максимум 30 000 долларов и, скорее всего, 25 000 долларов.
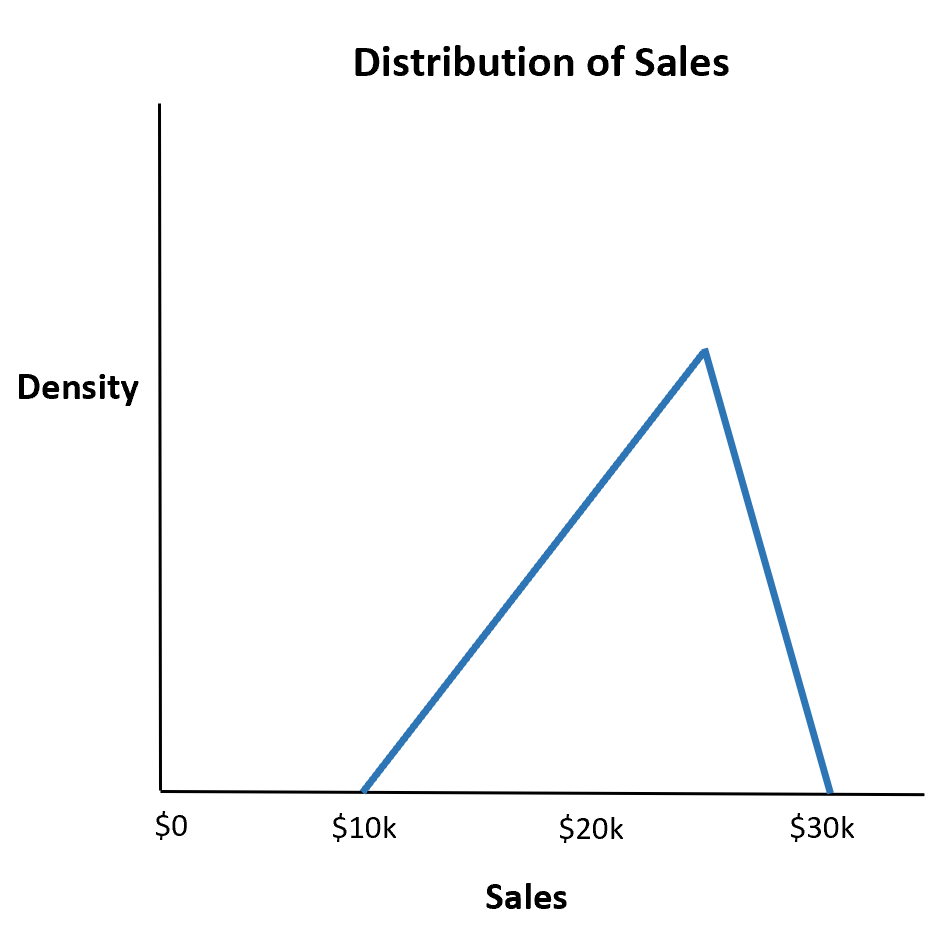
Какова вероятность того, что общий объем продаж ресторана составит менее 20 000 долларов?
Мы можем использовать следующий код для вычисления этой вероятности:
library (EnvStats)
#calculate probability
ptri(q = 20000, min = 10000, max = 30000, mode = 25000)
[1] 0.3333333
Вероятность того, что общий объем продаж ресторана составит менее 20 000 долларов, равна 0,333 .
Пример 2: Расчет вероятности больше некоторого значения
Предположим, магазин оценивает, что количество покупателей, которые войдут в данную неделю, будет минимум 500, максимум 2000 и, скорее всего, 1200.

Какова вероятность того, что за данную неделю в магазин зайдет более 1500 покупателей?
Мы можем использовать следующий код для вычисления этой вероятности:
library (EnvStats)
#calculate probability
1 - ptri(q = 1500, min = 500, max = 2000, mode = 1200)
[1] 0.2083333
Вероятность того, что в магазин войдут более 1500 покупателей, составляет около 0,208.
Примечание.Полную документацию по функции ptri() можно найти здесь .
Дополнительные ресурсы
В следующих руководствах объясняется, как работать с другими распределениями вероятностей в R:
Как использовать нормальное распределение в R
Как использовать биномиальное распределение в R
Как использовать распределение Пуассона в R
Как использовать полиномиальное распределение в R