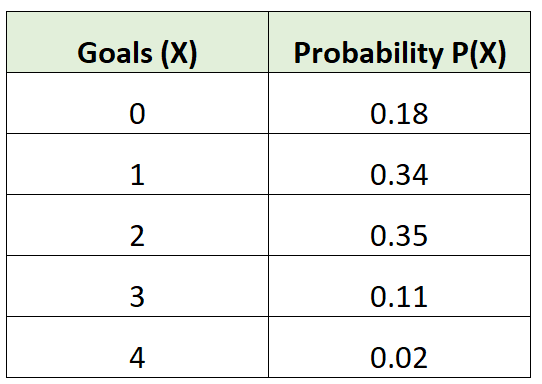
Распределение вероятностей говорит нам о вероятности того, что случайная величина примет определенные значения.
Например, следующее распределение вероятностей говорит нам о вероятности того, что определенная футбольная команда забьет определенное количество голов в данной игре:
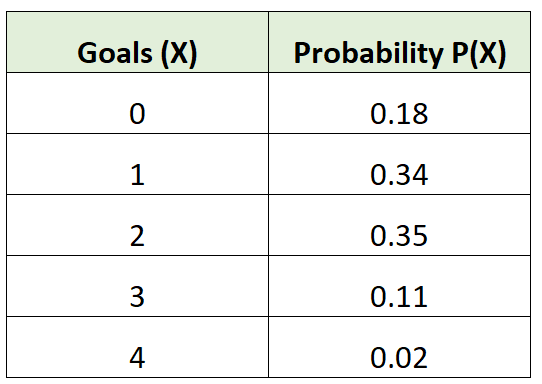
Чтобы найти дисперсию распределения вероятностей, мы можем использовать следующую формулу:
σ 2 = Σ(x i -μ) 2 * P(x i )
куда:
- x i : i -е значение
- μ: среднее значение распределения
- P(x i ): Вероятность i -го значения
Например, рассмотрим наше распределение вероятностей для футбольной команды:

Среднее количество голов для футбольной команды будет рассчитываться как:
μ = 0*0,18 + 1*0,34 + 2*0,35 + 3*0,11 + 4*0,02 = 1,45 гола.
Затем мы могли бы рассчитать дисперсию как:
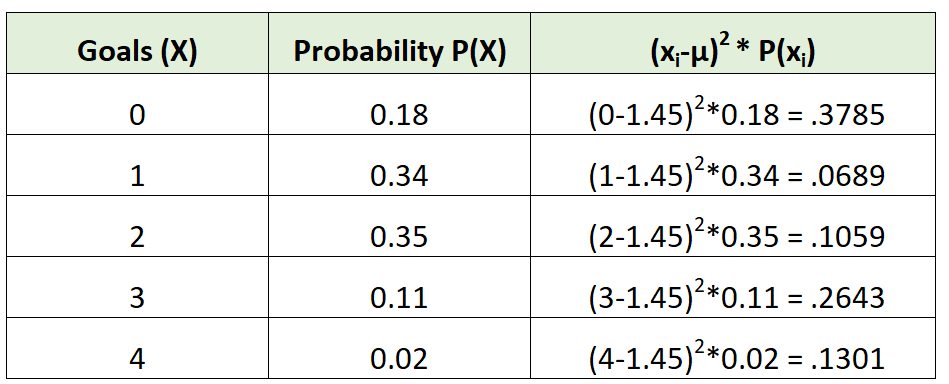
Дисперсия — это просто сумма значений в третьем столбце. Таким образом, мы будем рассчитывать его как:
σ 2 = 0,3785 + 0,0689 + 0,1059 + 0,2643 + 0,1301 = 0,9475
В следующих примерах показано, как рассчитать дисперсию распределения вероятностей в нескольких других сценариях.
Пример 1: Дисперсия отказов транспортных средств
Следующее распределение вероятностей говорит нам о вероятности того, что данное транспортное средство испытает определенное количество отказов батареи в течение 10-летнего периода:
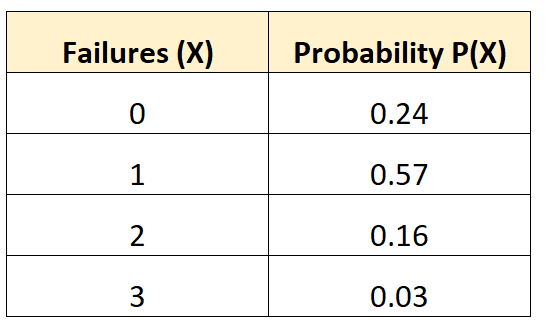
Чтобы найти дисперсию этого распределения вероятностей, нам нужно сначала вычислить среднее количество ожидаемых отказов:
μ = 0*0,24 + 1*0,57 + 2*0,16 + 3*0,03 = 0,98 отказов.
Затем мы могли бы рассчитать дисперсию как:
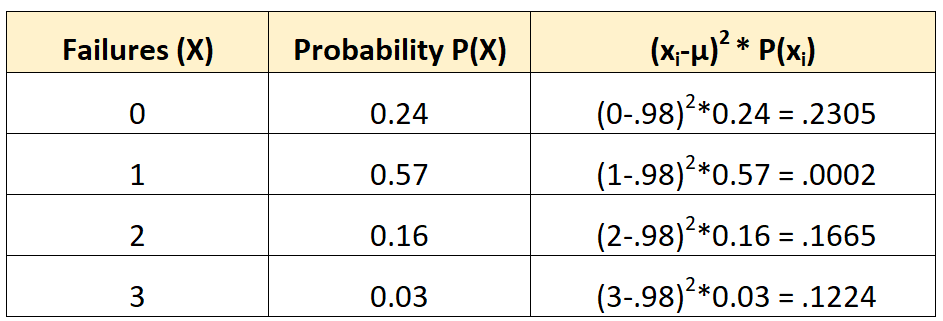
Дисперсия представляет собой сумму значений в третьем столбце. Таким образом, мы будем рассчитывать его как:
σ 2 = 0,2305 + 0,0002 + 0,1665 + 0,1224 = 0,5196
Пример 2: Отклонение продаж
Следующее распределение вероятностей говорит нам о вероятности того, что данный продавец совершит определенное количество продаж в предстоящем месяце:
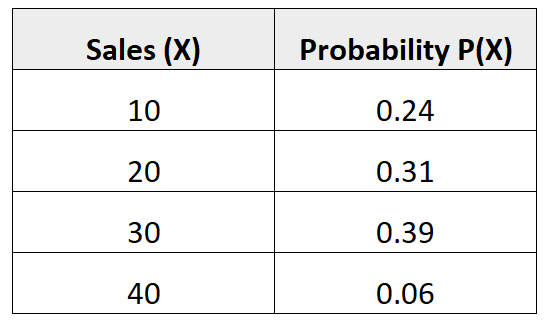
Чтобы найти дисперсию этого распределения вероятностей, нам нужно сначала вычислить среднее количество ожидаемых продаж:
μ = 10*0,24 + 20*0,31 + 30*0,39 + 40*0,06 = 22,7 продаж.
Затем мы могли бы рассчитать дисперсию как:
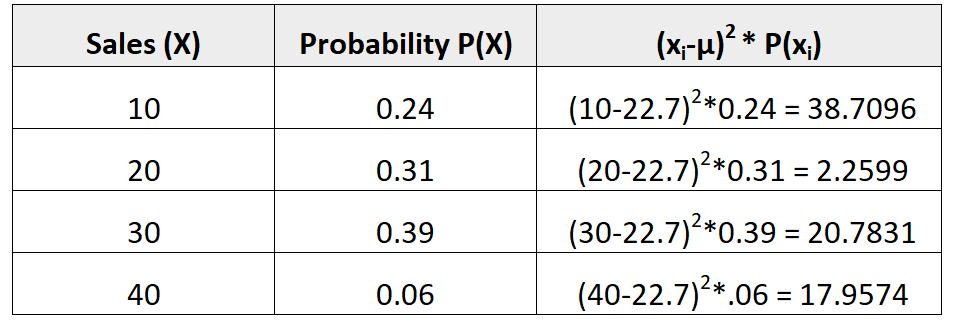
Дисперсия представляет собой сумму значений в третьем столбце. Таким образом, мы будем рассчитывать его как:
σ 2 = 38,7096 + 2,2599 + 20,7831 + 17,9574 = 79,71
Обратите внимание, что мы также можем использовать калькулятор распределения вероятностей для автоматического расчета дисперсии этого распределения:


Дисперсия составляет 79,71.Это соответствует значению, которое мы рассчитали вручную.