Корреляция используется для измерения линейной связи между двумя переменными.
Коэффициент корреляции всегда принимает значение от -1 до 1, где:
- -1 указывает на совершенно отрицательную линейную корреляцию между двумя переменными
- 0 указывает на отсутствие линейной корреляции между двумя переменными
- 1 указывает на совершенно положительную линейную корреляцию между двумя переменными.
У студентов часто возникает вопрос: когда мне следует использовать корреляцию?
Краткий ответ: используйте корреляцию, когда вы хотите количественно оценить линейную связь между двумя переменными, и ни одна из переменных не представляет собой переменную ответа или «результата» .
Следующие примеры показывают, когда вы должны и не должны использовать корреляцию на практике.
Пример 1: когда использовать корреляцию
Предположим, профессор хочет понять линейную зависимость между результатами экзаменов по математике и результатами экзаменов по естественным наукам для студентов его класса.
Например, учащиеся, получившие высокие баллы на экзамене по математике, также получают высокие баллы на экзамене по естественным наукам? Или учащиеся с высокими баллами по математике, как правило, имеют низкие баллы по естественным наукам?
В этом сценарии он мог бы вычислить корреляцию между результатами экзамена по математике и результатами экзамена по естественным наукам, потому что он просто хочет понять линейную связь между двумя переменными, и ни одна из переменных не может считаться переменной ответа.
Предположим, он вычислилкоэффициент корреляции Пирсона и обнаружил, что он равен r = 0,78. Это сильная положительная корреляция, которая означает, что учащиеся с высокими баллами по математике также, как правило, имеют высокие баллы по естественным наукам.
Пример 2. Когда не следует использовать корреляцию
Предположим, что отдел маркетинга какой-то компании хочет количественно определить, как расходы на рекламу влияют на общий доход.
Например, на каждый дополнительный доллар, потраченный на рекламу, какую дополнительную прибыль может получить компания?
В этом сценарии отдел должен использовать модель линейной регрессии для количественной оценки взаимосвязи между расходами на рекламу и общим доходом, поскольку переменная «доход» является переменной ответа.
Предположим, отдел подходит к простой модели линейной регрессии и считает, что следующее уравнение лучше всего описывает взаимосвязь между расходами на рекламу и общим доходом:
Общий доход = 145,4 + 0,34 * (расходы на рекламу)
Мы интерпретируем это так, что каждый дополнительный доллар, потраченный на рекламу, приводит к среднему увеличению общего дохода на 0,34 доллара.
Предостережения по использованию корреляции
Важно отметить, что корреляцию можно использовать только для количественной оценки линейной зависимости между двумя переменными.
Однако в некоторых случаях коэффициент корреляции не может эффективно отразить взаимосвязь между двумя переменными, имеющими нелинейную взаимосвязь.
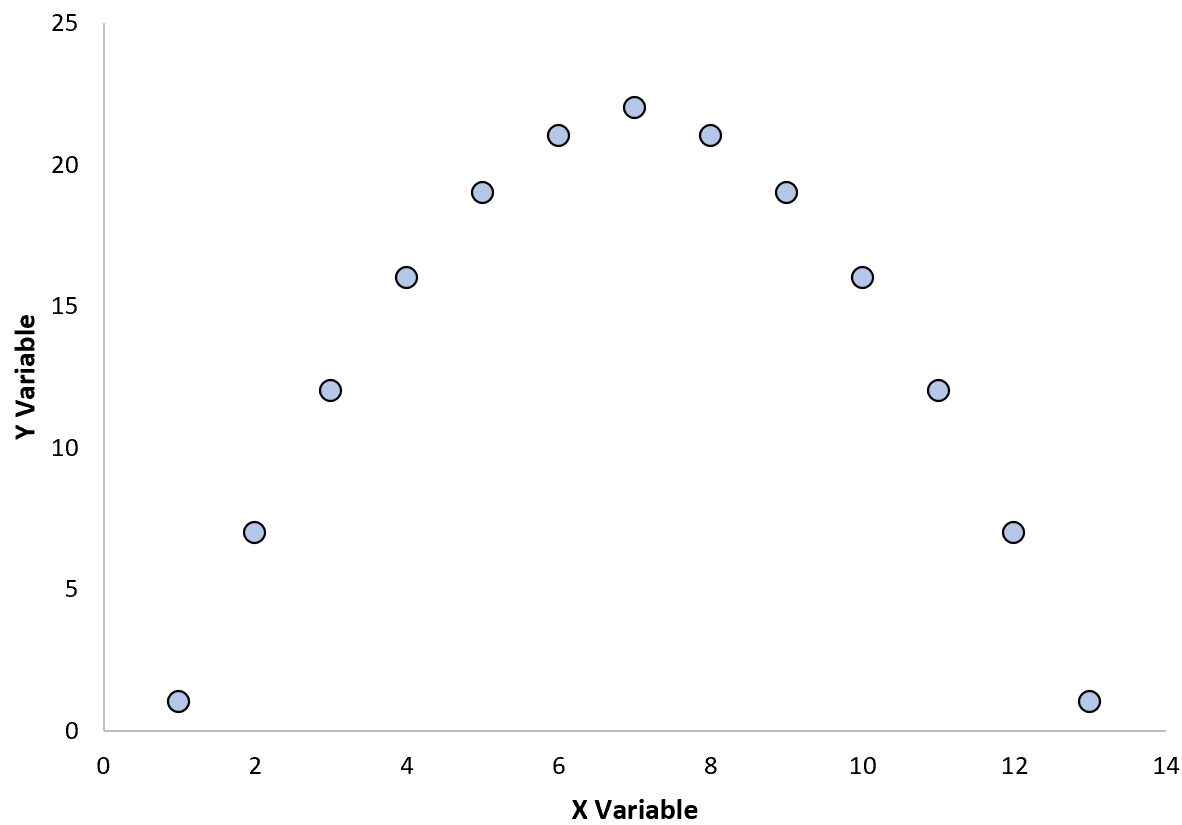
Например, предположим, что мы создали следующую диаграмму рассеяния, чтобы визуализировать взаимосвязь между двумя переменными:
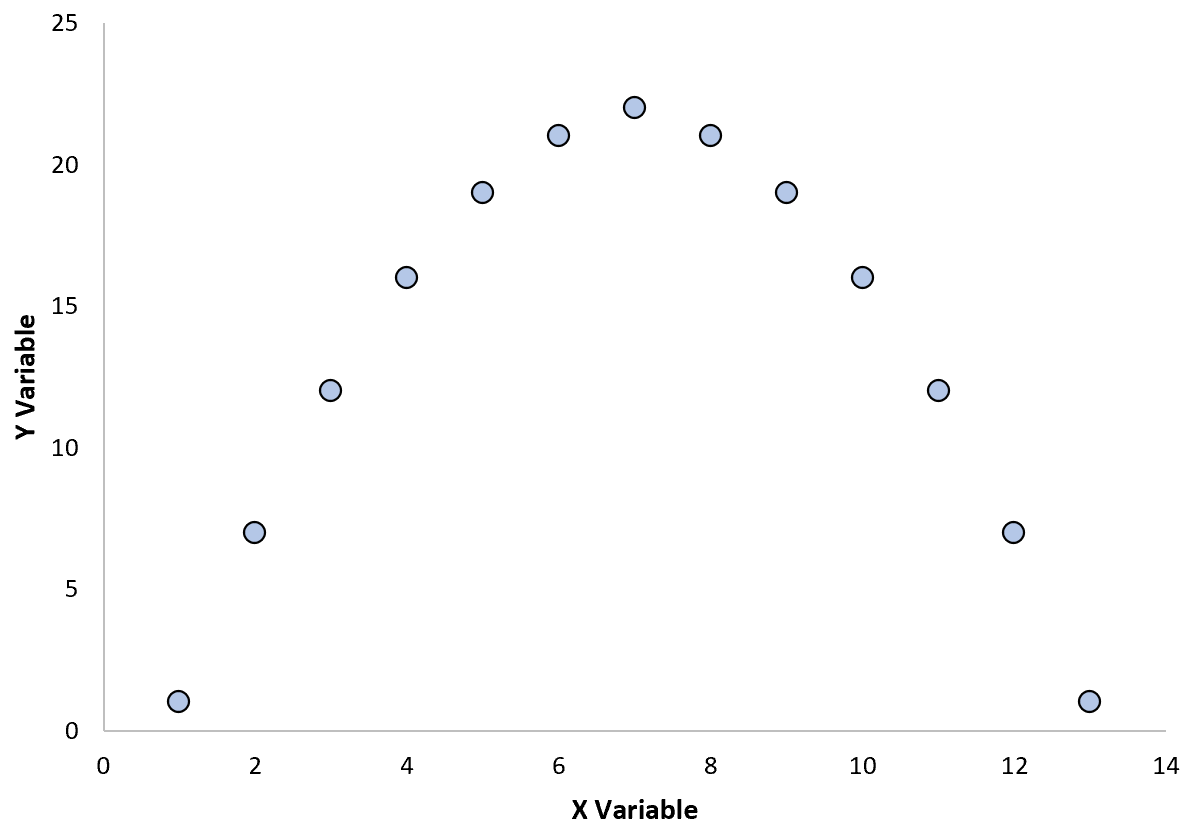
Если вычислить коэффициент корреляции между этими двумя переменными, окажется, что r = 0. Это означает, что между двумя переменными нет линейной зависимости.
Однако из графика видно, что две переменные имеют отношение — просто оно квадратичное, а не линейное.
Таким образом, когда вы вычисляете корреляцию между двумя переменными, имейте в виду, что может быть полезно создать диаграмму рассеяния, чтобы визуализировать взаимосвязь между переменными.
Даже если две переменные не имеют линейной связи, вполне возможно, что они могут иметь нелинейную связь, которая будет показана на диаграмме рассеяния.
Дополнительные ресурсы
В следующих руководствах объясняется, как корреляция используется в различных обстоятельствах:
6 примеров корреляции в реальной жизни
Что считается «сильной» корреляцией?
Корреляция против ассоциации: в чем разница?
Корреляция против регрессии: в чем разница?