Критерий знакового ранга Уилкоксона — это непараметрическая версия парного t-критерия.Он используется для проверки наличия значительной разницы между двумя средними значениями генеральной совокупности, когда распределение различий между двумя выборками нельзя считать нормальным.
В этом руководстве объясняется, как провести знаковый ранговый тест Уилкоксона в R.
Пример. Критерий знакового ранга Уилкоксона в R
Предположим, тренер по баскетболу хочет знать, увеличивает ли определенная программа тренировок количество штрафных бросков, выполняемых его игроками. Чтобы проверить это, он попросил 15 игроков выполнить по 20 штрафных бросков до и после тренировочной программы.
Поскольку каждый игрок может быть «спарен» сам с собой, тренер планировал использовать парный t-критерий, чтобы определить, была ли существенная разница между средним количеством штрафных бросков, выполненных до и после тренировочной программы. Однако распределение различий оказывается ненормальным, поэтому вместо этого тренер использует критерий знакового ранга Уилкоксона.
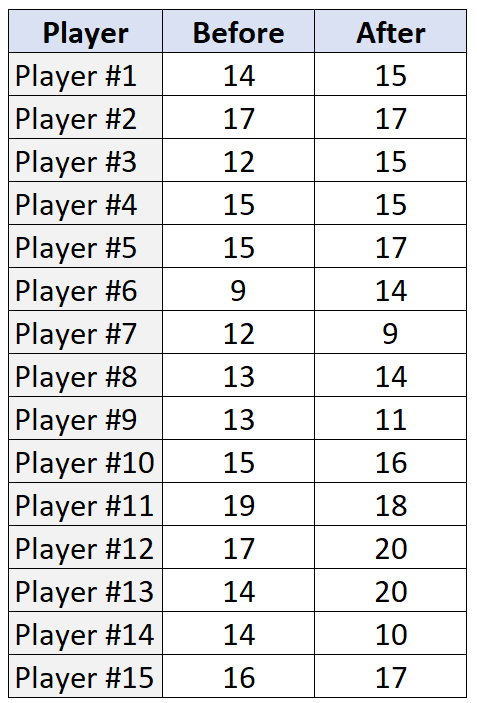
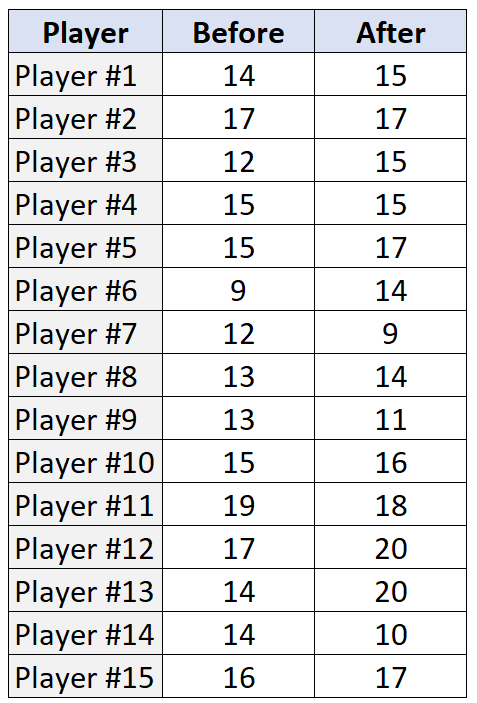
В следующей таблице показано количество штрафных бросков, выполненных (из 20 попыток) каждым из 15 игроков как до, так и после тренировочной программы:
Чтобы выполнить знаковый ранговый тест Уилкоксона для этих данных в R, мы можем использовать функцию wilcox.test() , которая использует следующий синтаксис:
wilkox.test(x, y, парный = TRUE)
куда:
- x, y: два вектора значений данных
- парный: установка этого параметра в TRUE сообщает R, что наши два вектора содержат парные данные.
В следующем коде показано, как использовать эту функцию для выполнения критерия знакового ранга Уилкоксона для этих данных:
#create the two vectors of data
before <- c(14, 17, 12, 15, 15, 9, 12, 13, 13, 15, 19, 17, 14, 14, 16)
after <- c(15, 17, 15, 15, 17, 14, 9, 14, 11, 16, 18, 20, 20, 10, 17)
#perform Wilcoxon Signed-Rank Test
wilcox.test(before, after, paired=TRUE)
Wilcoxon signed rank test with continuity correction
data: before and after
V = 29.5, p-value = 0.275
alternative hypothesis: true location shift is not equal to 0
Статистика теста составляет 29,5 , а соответствующее значение p равно 0,275.Поскольку это p-значение не меньше 0,05, мы не можем отвергнуть нулевую гипотезу. Нет статистически значимой разницы в количестве штрафных бросков до и после участия игроков в тренировочной программе.
По умолчанию эта функция выполняет двусторонний знаковый ранговый критерий Уилкоксона, но вы можете указать левосторонний или правосторонний критерий, используя альтернативный аргумент:
#perform left-tailed Wilcoxon Signed-Rank Test
wilcox.test(before, after, paired=TRUE, alternative="less")
Wilcoxon signed rank test with continuity correction
data: before and after
V = 29.5, p-value = 0.1375
alternative hypothesis: true location shift is less than 0
#perform right-tailed Wilcoxon Signed-Rank Test
wilcox.test(before, after, paired=TRUE, alternative="greater")
Wilcoxon signed rank test with continuity correction
data: before and after
V = 29.5, p-value = 0.8774
alternative hypothesis: true location shift is greater than 0
Дополнительные ресурсы
Введение в критерий знакового ранга Уилкоксона
Калькулятор критерия знакового ранга Уилкоксона