ANOVA («дисперсионный анализ») — это тип модели, который используется для определения того, существует ли значительная разница между средними значениями трех или более независимых групп.
Всякий раз, когда мы подгоняем модель ANOVA к набору данных, всегда будут остатки — они представляют собой разницу между каждым отдельным наблюдением и средним значением группы, из которой было получено наблюдение.
В следующем примере показано, как вычислить остатки для модели ANOVA на практике.
Пример: расчет остатков в ANOVA
Предположим, мы набираем 90 человек для участия в эксперименте по снижению веса, в котором мы случайным образом назначаем 30 человек следовать либо программе А, либо программе Б, либо программе С в течение одного месяца.
Мы можем провести односторонний дисперсионный анализ, чтобы определить, есть ли статистически значимая разница между результирующей потерей веса по трем программам.
Предположим, мы рассчитали среднюю потерю веса для участников каждой программы:
- Программа А : 1,58 фунта
- Программа B : 2,56 фунта
- Программа C : 4,13 фунта
Остатки для модели ANOVA будут представлять собой разницу между потерей веса каждого человека и средней потерей веса в их программе.
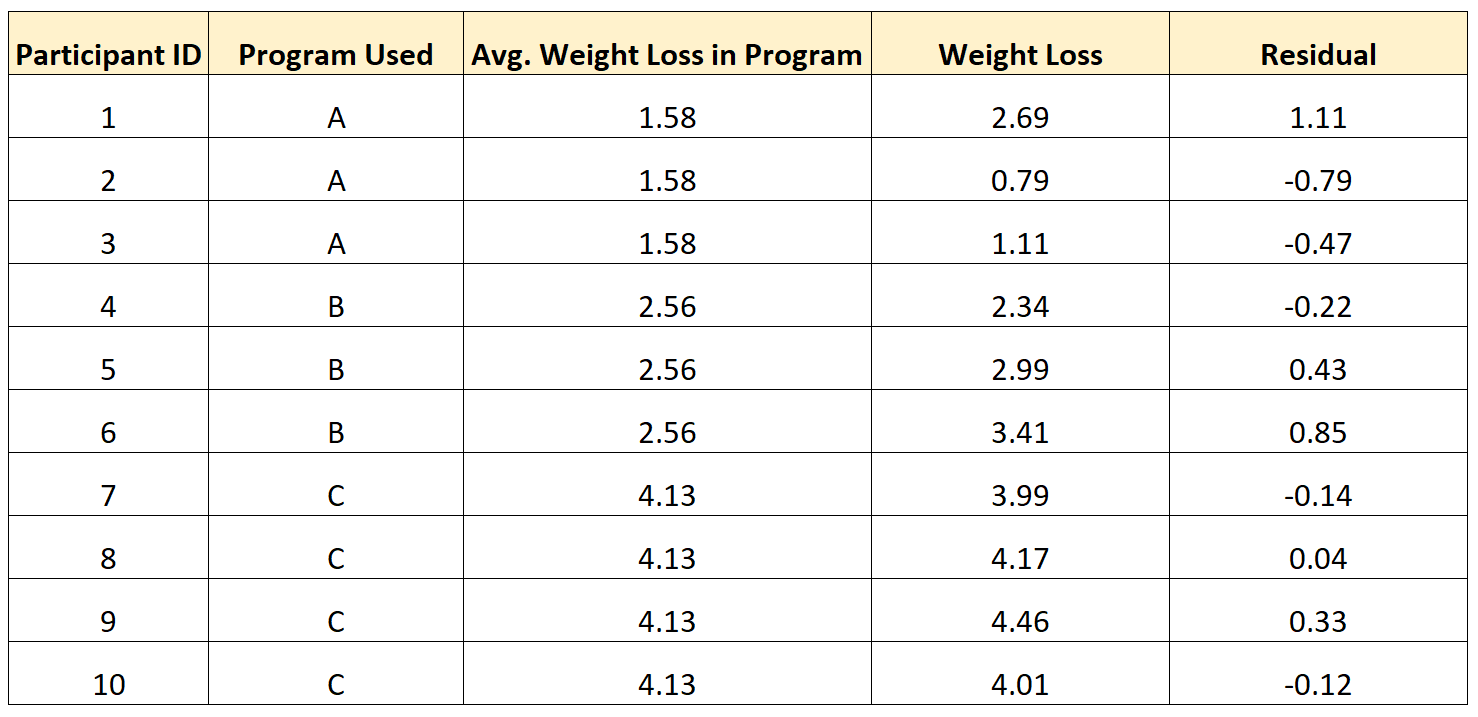
Например, в следующей таблице показано, как рассчитать остатки для 10 разных участников исследования:

Обратите внимание на следующую закономерность:
- Лица, значение которых превышало среднее значение их группы, имели положительную невязку .
- Лица, у которых значение было меньше, чем среднее значение их группы, имели отрицательный остаток .
На практике мы рассчитали бы остатки для всех 90 человек.
Как использовать остатки для проверки нормальности
Одно из предположений дисперсионного анализа состоит в том, что остатки распределены нормально.
Самый распространенный способ проверить это предположение — создать график QQ .
Если остатки распределены нормально, то точки на графике QQ будут лежать на прямой диагональной линии.
Вот как будет выглядеть график QQ для нашего предыдущего примера:
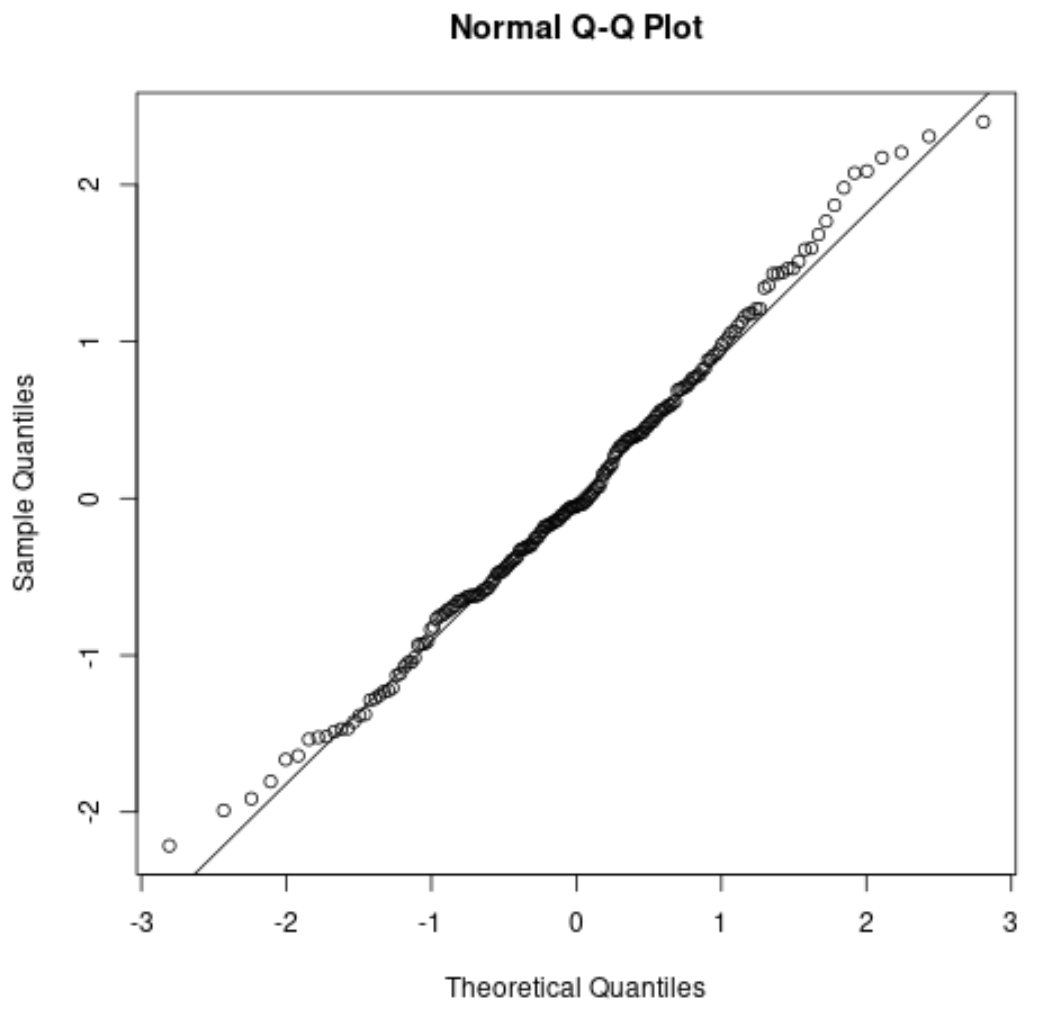
Точки немного отклоняются от прямой диагональной линии на хвостовых концах, но в целом точки довольно хорошо следуют диагональной линии. Это говорит нам о том, что предположение о нормальности, вероятно, выполнено.
В качестве справки, вот как может выглядеть график QQ для ненормально распределенных остатков:
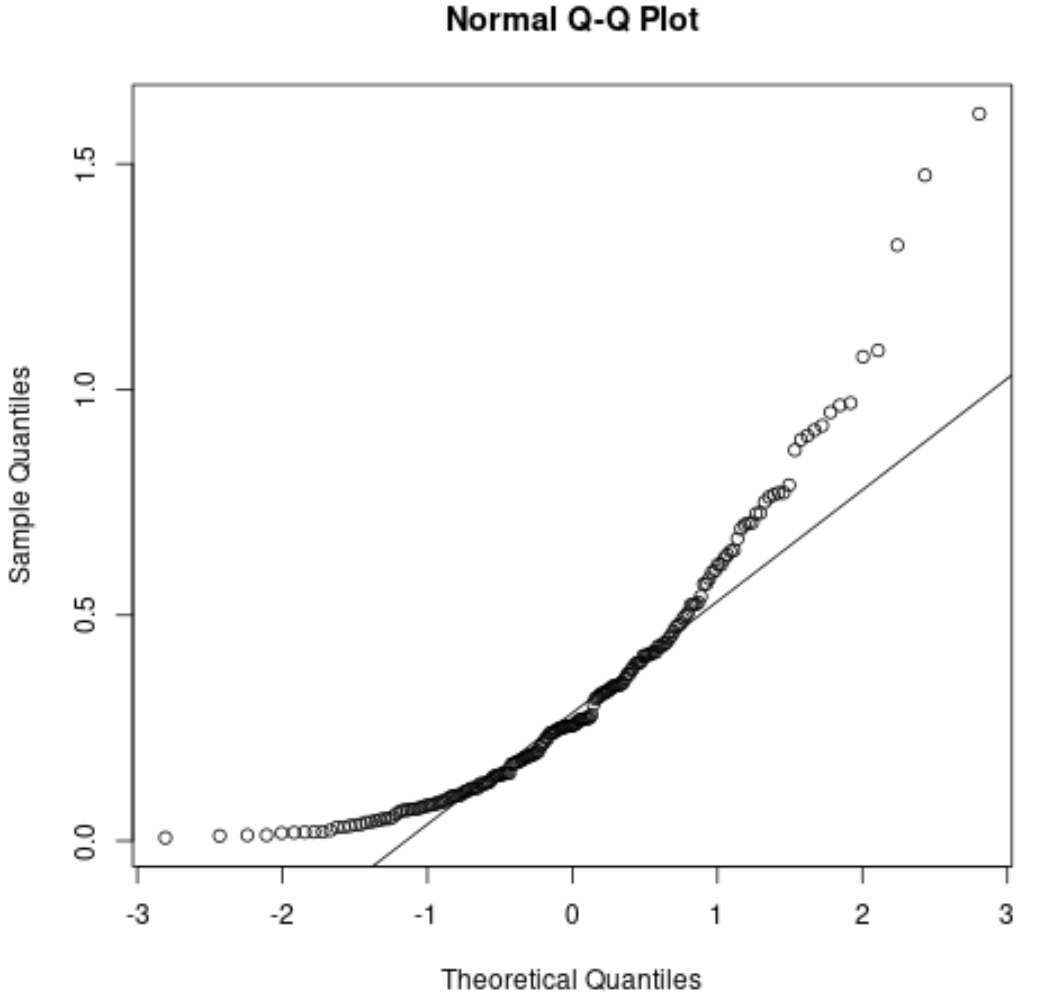
Точки сильно отклоняются от прямой диагональной линии, что указывает на то, что остатки не распределены нормально.
Обратитесь к следующим учебным пособиям, чтобы узнать, как создавать графики QQ в другом программном обеспечении:
Дополнительные ресурсы
Следующие статьи предоставляют дополнительную информацию о моделях ANOVA:
Введение в однофакторный дисперсионный анализ
Как проверить предположения ANOVA
4 примера использования ANOVA в реальной жизни