Теорема Байеса утверждает следующее для любых двух событий A и B :
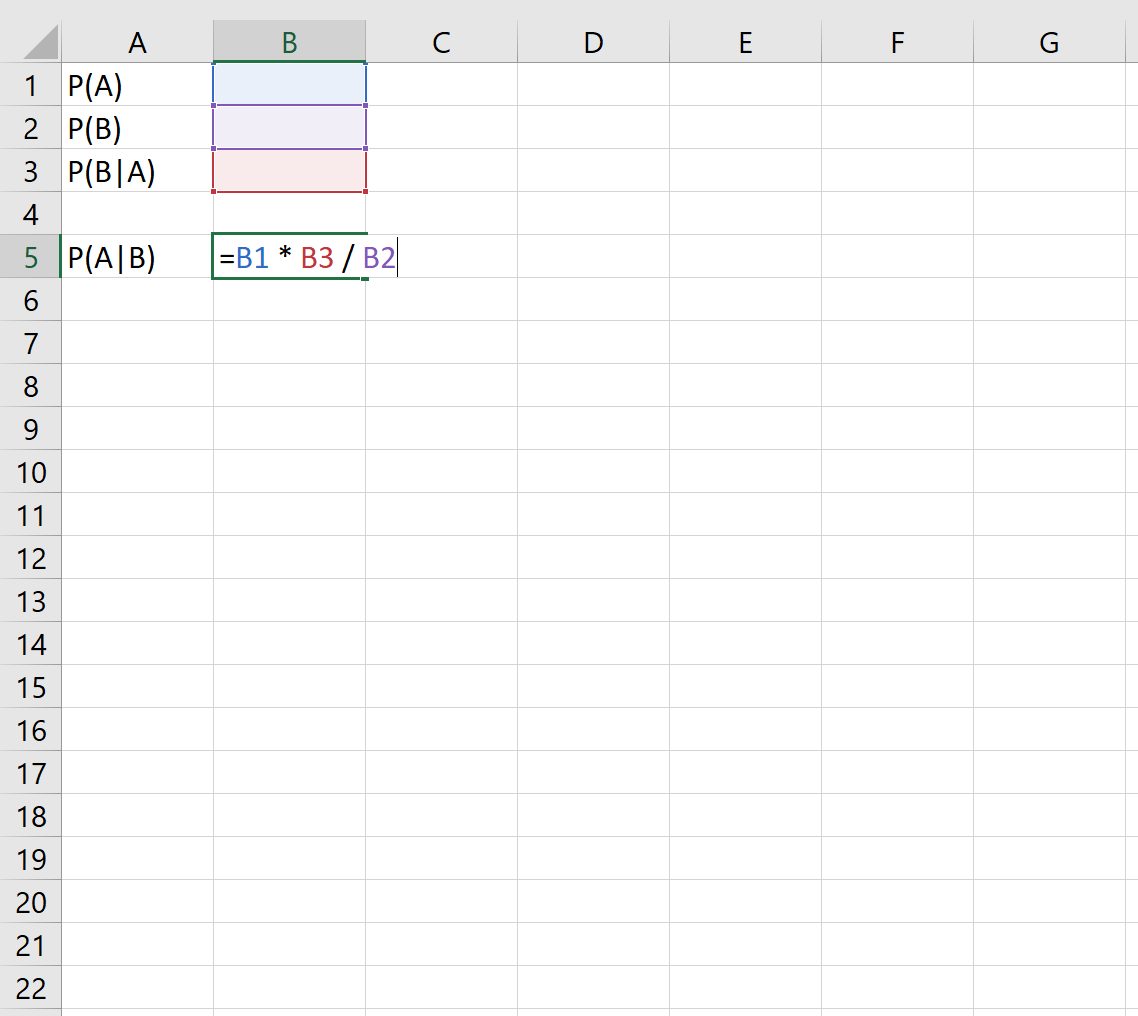
Р(А|В) = Р(А)*Р(В|А) / Р(В)
куда:
- P(A|B): Вероятность события A при условии, что произошло событие B.
- P(B|A): Вероятность события B при условии, что произошло событие A.
- P(A): Вероятность события A.
- P(B): Вероятность события B.
Например, предположим, что вероятность того, что погода будет облачной, составляет 40%. Также предположим, что вероятность дождя в данный день составляет 20 %, а вероятность облаков в дождливый день — 85 %.
Если в данный день на улице облачно, какова вероятность того, что в этот день пойдет дождь?
Решение :
- Р(облачно) = 0,40
- P(дождь) = 0,20
- P(облачно | дождь) = 0,85
Таким образом, мы можем рассчитать:
- P(дождь | облачно) = P(дождь) * P(облачно | дождь) / P(облачно)
- P(дождь | облачно) = 0,20 * 0,85 / 0,40
- P(дождь | облачно) = 0,425
Если в данный день на улице облачно, вероятность того, что в этот день пойдет дождь, составляет 0,425 или 42,5% .
В следующем примере показано, как решить именно эту задачу с помощью теоремы Байеса в Excel.
Пример: теорема Байеса в Excel
Следующая формула показывает, как применить теорему Байеса в Excel:
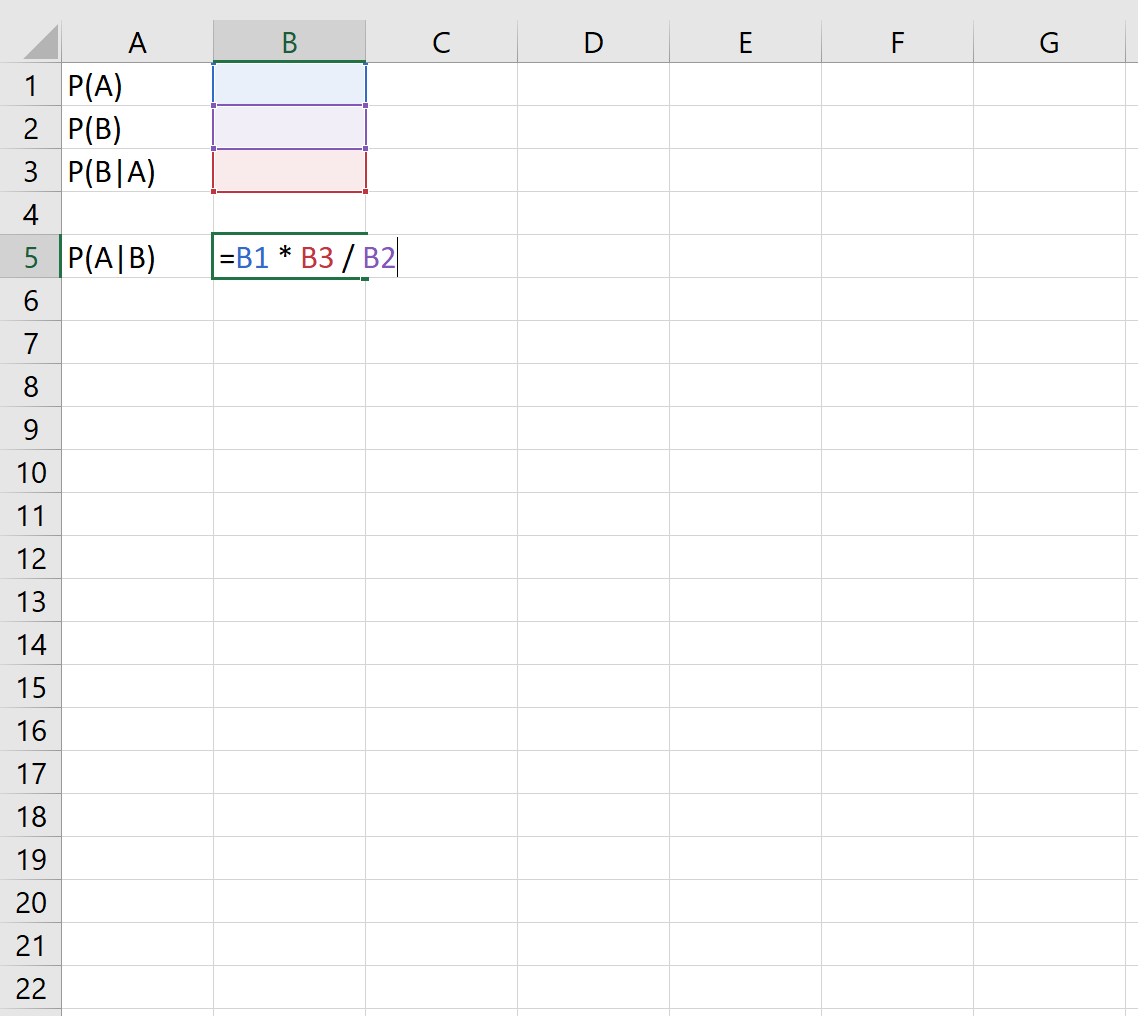
Например, если мы знаем следующие вероятности:
- Р(облачно) = 0,40
- P(дождь) = 0,20
- P(облачно | дождь) = 0,85
Затем мы можем просто вставить их в ячейки в Excel:
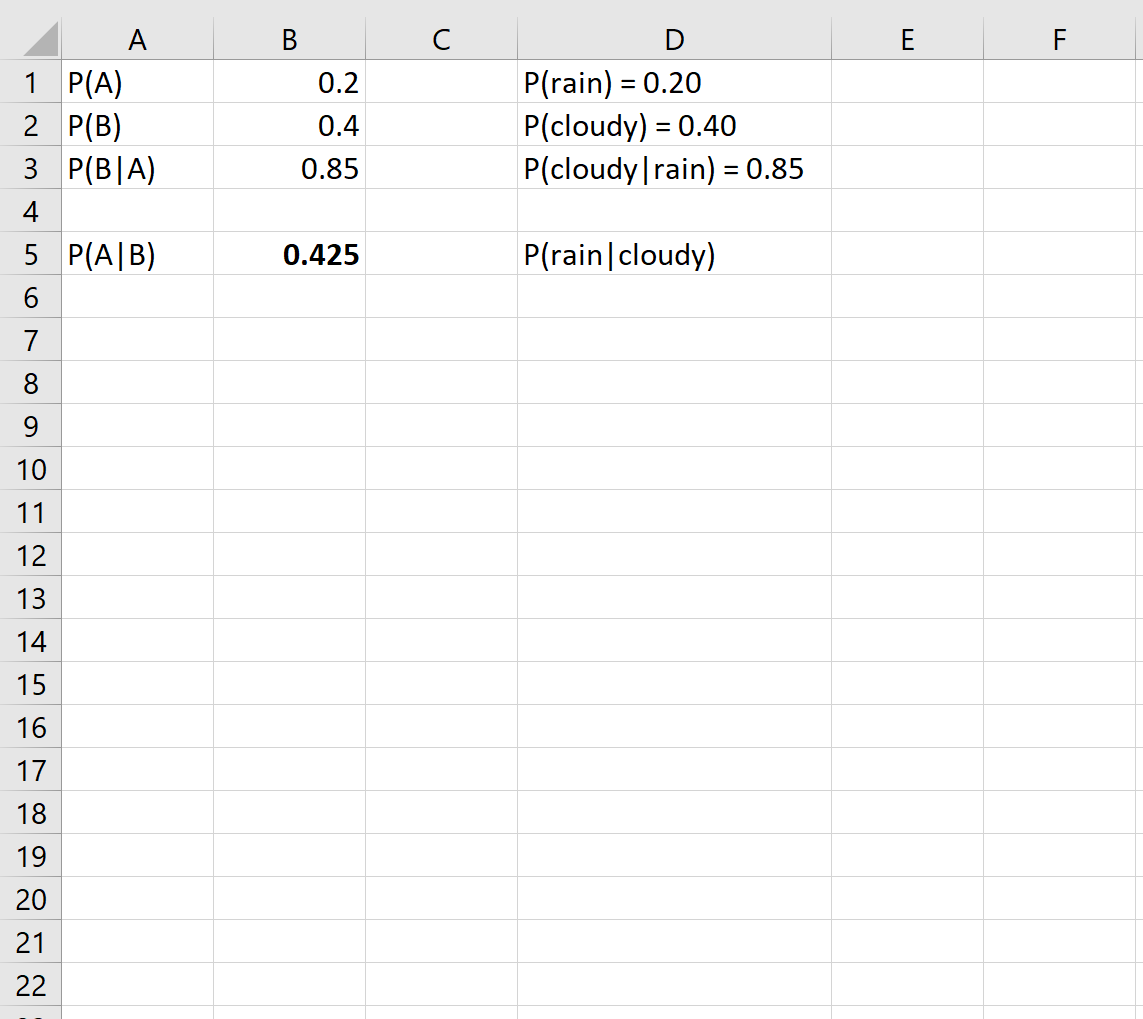
Это говорит нам о том, что если в данный день на улице облачно, вероятность того, что в этот день пойдет дождь, составляет 0,425 или 42,5% .
Дополнительные ресурсы
Как рассчитать условную вероятность в Excel
Как применить эмпирическое правило в Excel
Как применить центральную предельную теорему в Excel