Центральная предельная теорема утверждает, что выборочное распределение среднего значения выборки приблизительно нормально, если размер выборки достаточно велик, даже если распределение населения не является нормальным .
Центральная предельная теорема также утверждает, что выборочное распределение будет иметь следующие свойства:
1. Среднее значение выборочного распределения будет равно среднему значению распределения генеральной совокупности:
х = μ
2. Стандартное отклонение выборочного распределения будет равно стандартному отклонению генеральной совокупности, деленному на объем выборки:
с = σ / √ п
В этом руководстве мы объясним, как применить центральную предельную теорему в Excel к заданному распределению.
Применение центральной предельной теоремы в Excel
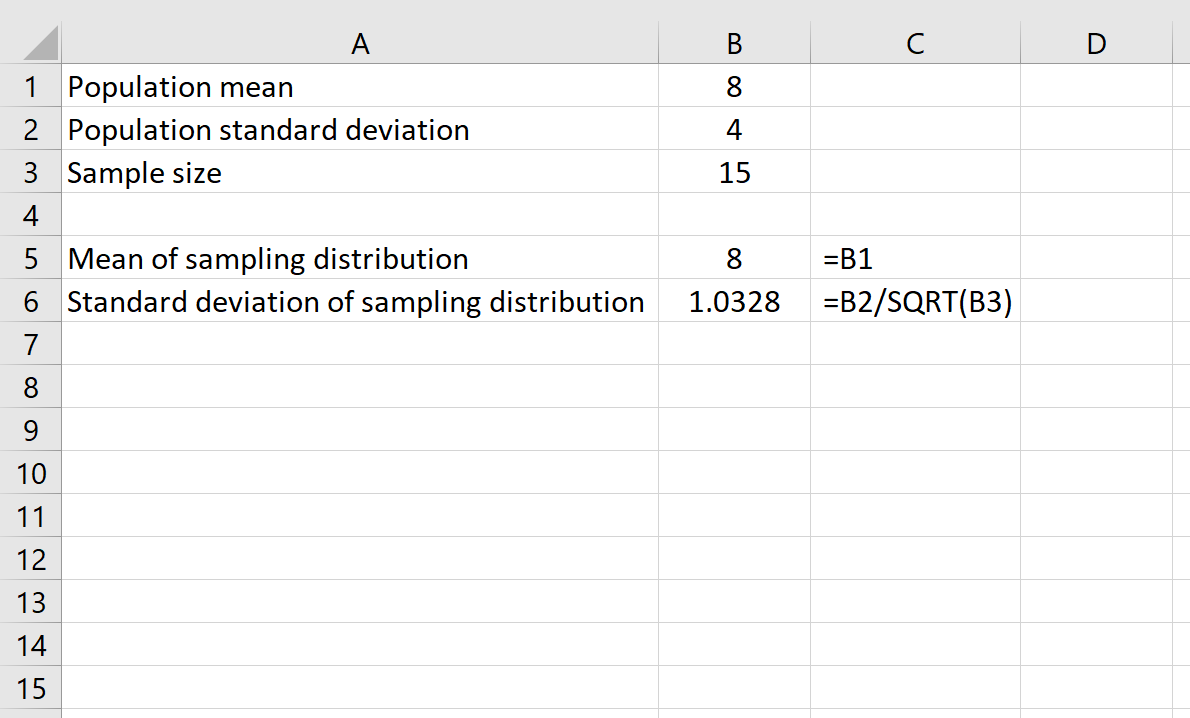
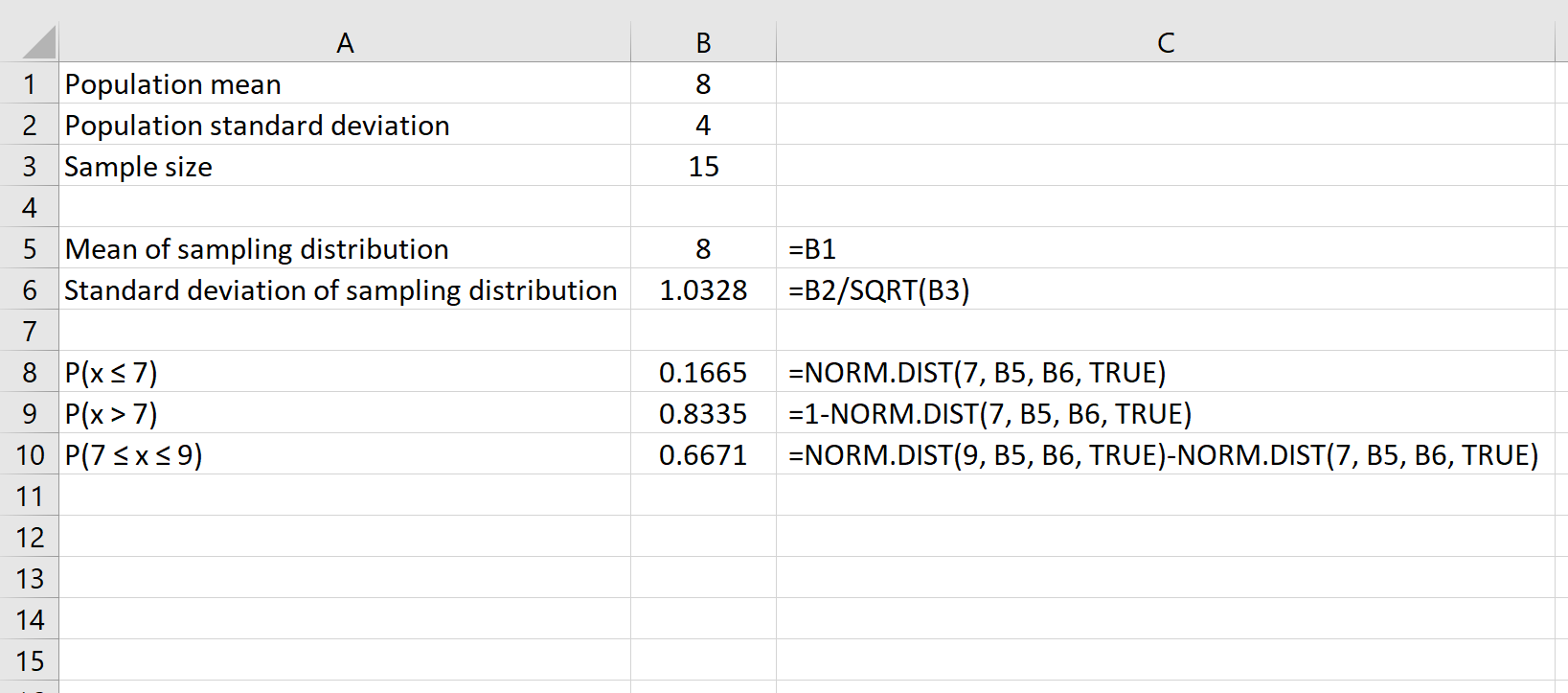
Предположим, у нас есть распределение со средним значением 8 и стандартным отклонением 4.Мы можем использовать следующие формулы в Excel, чтобы найти как среднее значение, так и стандартное отклонение выборочного распределения с размером выборки 15 :
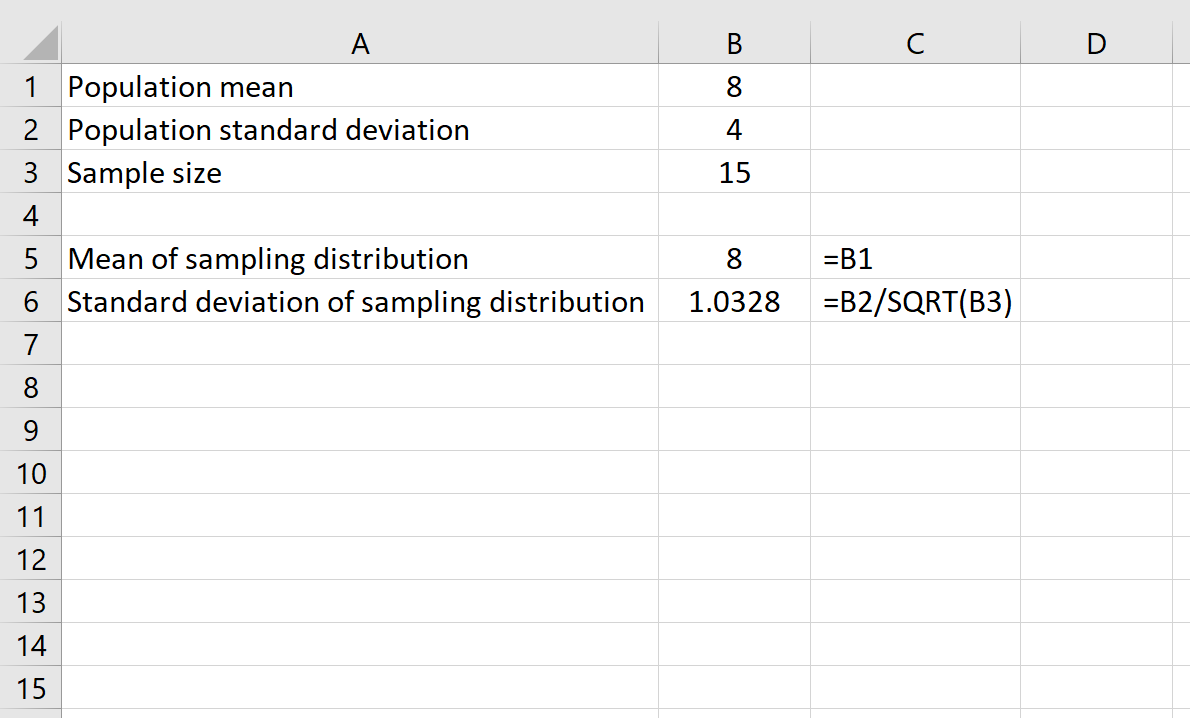
Среднее значение распределения выборки просто равно среднему значению распределения генеральной совокупности, равному 8 .
Стандартное отклонение выборочного распределения равно стандартному отклонению генеральной совокупности, деленному на размер выборки, то есть: 4 /√15 = 1,0328 .
Мы также можем использовать центральную предельную теорему, чтобы ответить на вопросы о вероятностях. Например, если данная совокупность имеет среднее значение 8 и стандартное отклонение 4 , какова вероятность того, что данная выборка размером 15имеет среднее значение меньше или равно 7 ?
Чтобы ответить на этот вопрос, мы можем использовать функцию НОРМ.РАСП() в Excel, которая использует следующий синтаксис:
НОРМ.РАСП(x, среднее, стандартное_отклонение, кумулятивное)
куда:
- x: образец означает, что вы хотите протестировать
- среднее значение: ожидаемое среднее значение выборочного распределения
- standard_dev: ожидаемое стандартное отклонение выборочного распределения.
- кумулятивный: TRUE возвращает значение обычного CDF; FALSE возвращает значение обычного Pdf.В нашем случае мы всегда будем использовать TRUE.
Эта функция вернет вероятность того, что среднее значение выборки меньше или равно определенному значению.
Вот формула, которую мы будем использовать в этом примере:
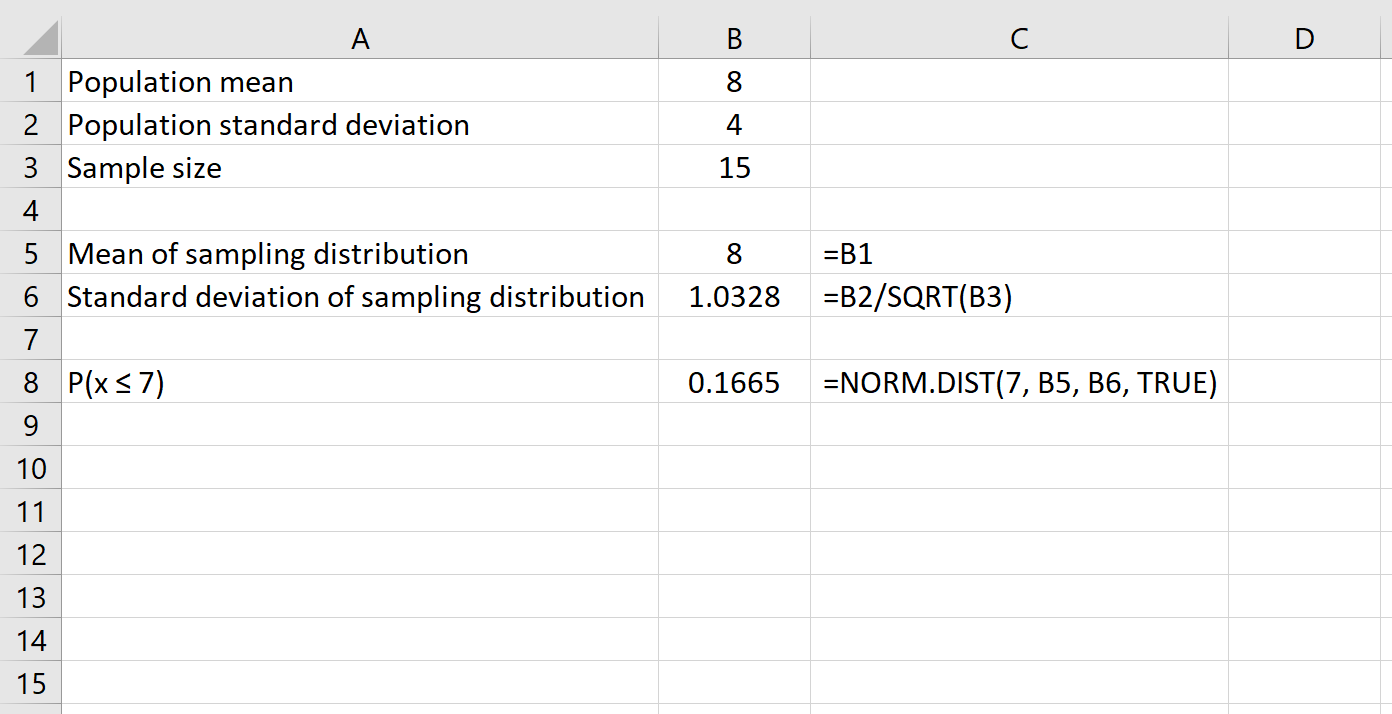
Это говорит нам о том, что для совокупности со средним значением 8 и стандартным отклонением 4 вероятность того, что данная выборка размером 15имеет среднее значение, меньшее или равное 7 , равно 0,1665 .
Мы также можем найти вероятность того, что данный размер выборки имеет среднее значение больше определенного числа, просто используя формулу 1 – НОРМ.РАСП() .
Например, следующая формула показывает, как найти вероятность того, что для данного размера выборки, равного 15, среднее значение больше 7:
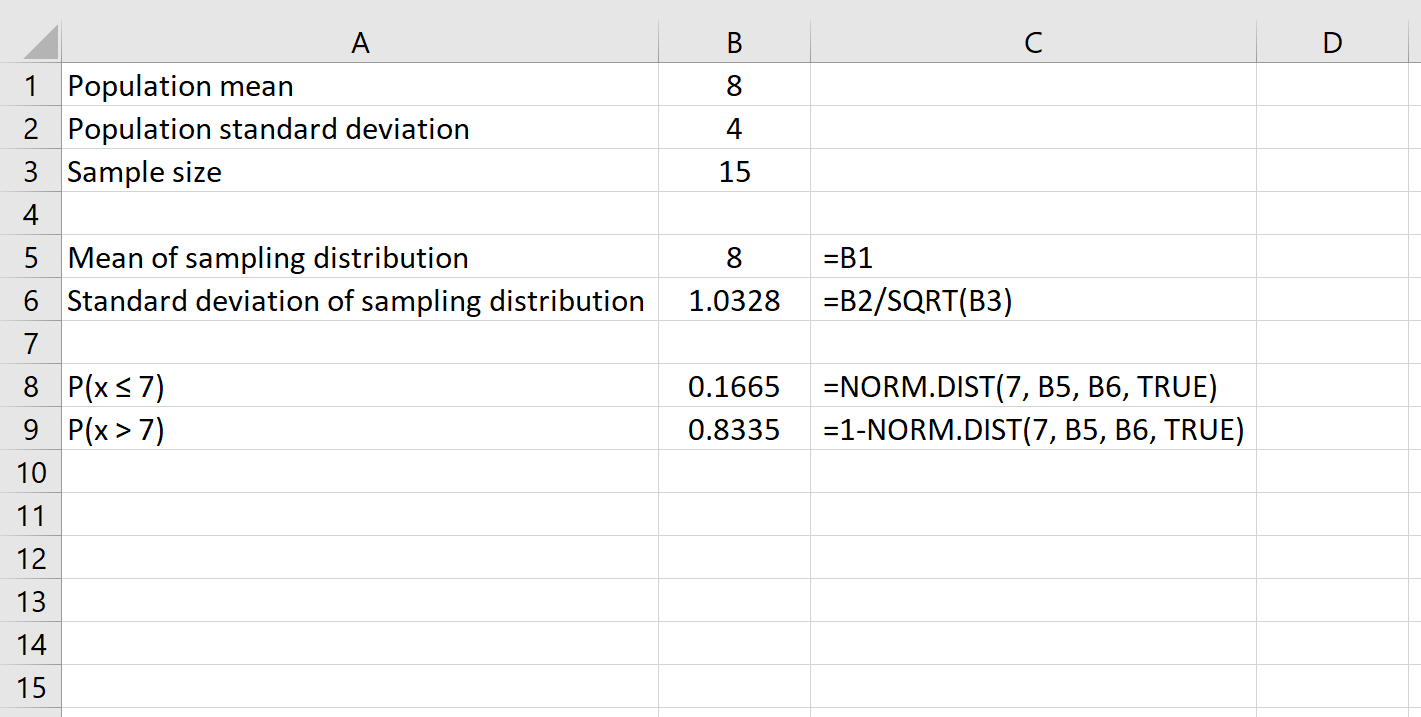
Наконец, мы можем найти вероятность того, что данный размер выборки будет иметь среднее значение между двумя числами, используя формулу НОРМ.РАСП(большее число) – НОРМ.РАСП(меньшее число) .
Например, следующая формула показывает, как найти вероятность того, что заданный размер выборки 15 имеет среднее значение между 7 и 9:
Дополнительные ресурсы
Калькулятор центральной предельной теоремы
Как применить эмпирическое правило в Excel
Как сделать кривую нормального распределения в Excel