Всякий раз, когда вы проводите статистическую проверку, вполне возможно, что чисто случайно вы получите значение p меньше 0,05, даже если ваша нулевая гипотеза верна.
Например, предположим, что вы хотите узнать, имеет ли определенное растение среднюю высоту более 10 дюймов. Ваши нулевая и альтернативная гипотезы для теста будут:
H 0 : μ = 10 дюймов
H A : μ > 10 дюймов
Чтобы проверить эту гипотезу, вы можете взять случайную выборку из 20 растений для измерения. Даже если истинная средняя высота этого вида растений составляет 10 дюймов, вполне возможно, что вы могли выбрать образец из 20 растений, которые были необычно высокими, что заставит вас отвергнуть нулевую гипотезу.
Хотя нулевая гипотеза была верна (средняя высота этого растения действительно составляла 10 дюймов), вы ее отвергли. В статистике мы называем это «ложным открытием». Вы утверждали, что сделали открытие — «значительный результат», — но на самом деле это ложное открытие.
Теперь представьте, что вы проводите сразу 100 статистических тестов. Используя альфа-уровень 0,05, вероятность ложного обнаружения для любого отдельного теста составляет всего 5%, но, поскольку вы проводите такое большое количество тестов, вы ожидаете, что около 5 из 100 приведут к ложным открытиям.
В современном мире ложные открытия могут быть распространенной проблемой, поскольку технологии позволяют исследователям проводить сотни или даже тысячи статистических тестов одновременно.
Например, исследователи-медики могут одновременно проводить статистические тесты десятков тысяч генов. Даже если уровень ложных срабатываний составляет всего 5 %, это означает, что сотни тестов могут привести к ложным срабатываниям.
Один из способов контролировать частоту ложных открытий — использовать так называемую процедуру Бенджамини-Хохберга.
Процедура Бенджамини-Хохберга
Процедура Бенджамини-Хохберга работает следующим образом:
Шаг 1: Проведите все свои статистические тесты и найдите p-значение для каждого теста.
Шаг 2: Расположите p-значения в порядке от наименьшего к наибольшему, присвоив каждому из них ранг — наименьшее p-значение имеет ранг 1, следующее наименьшее — ранг 2 и т. д.
Шаг 3: Рассчитайте критическое значение Бенджамини-Хохберга для каждого p-значения, используя формулу (i/m)*Q
куда:
i = ранг p-значения
m = общее количество тестов
Q = выбранная вами частота ложных обнаружений
Шаг 4: Найдите наибольшее значение p, которое меньше критического значения. Обозначьте каждое p-значение, которое меньше этого p-значения, значимым.
В следующем примере показано, как выполнить эту процедуру с конкретными значениями.
Пример
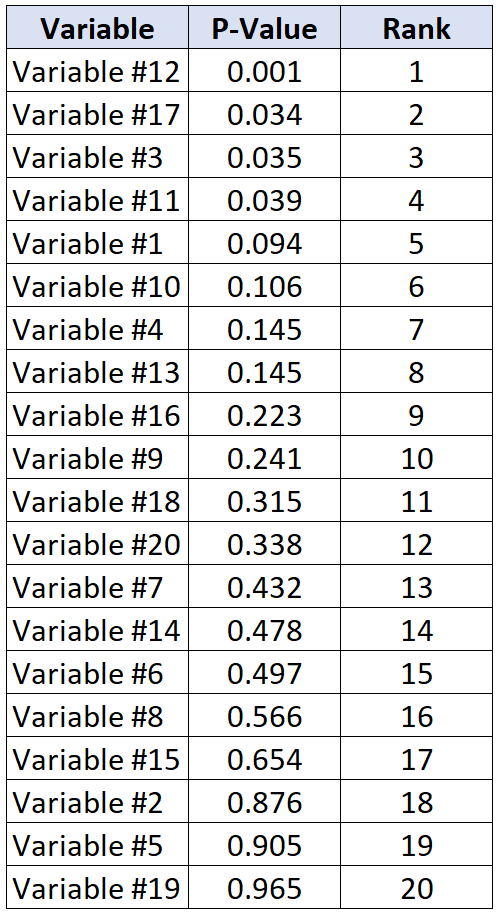
Предположим, исследователи заинтересованы в том, чтобы определить, связаны ли 20 различных переменных с сердечными заболеваниями. Они проводят сразу 20 отдельных статистических тестов и получают p-значение для каждого теста. В следующей таблице показаны p-значения для каждого теста, ранжированные в порядке от наименьшего к наибольшему.
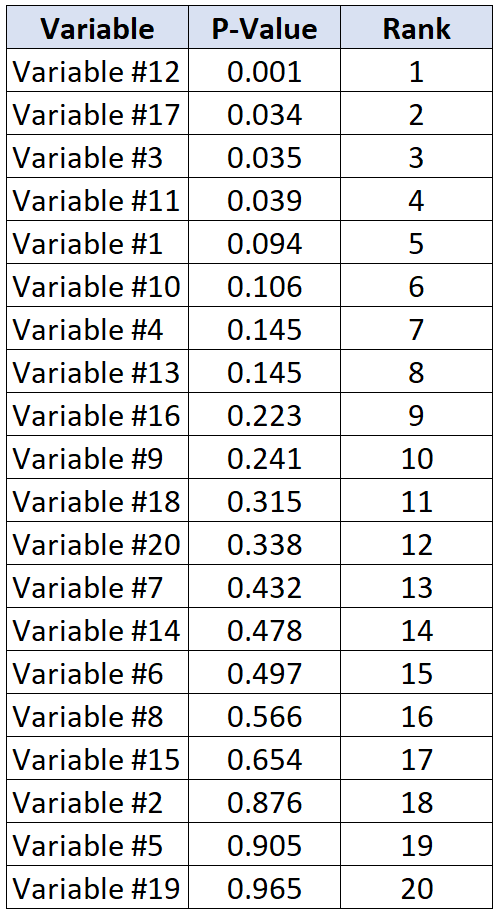
Предположим, что исследователи готовы принять 20% ложных открытий. Таким образом, чтобы вычислить критическое значение Бенджамини-Хохберга для каждого p-значения, мы можем использовать следующую формулу: (i/20)*0,2, где i = ранг p-значения.
В следующей таблице показано критическое значение Бенджамини-Хохберга для каждого отдельного p-значения:
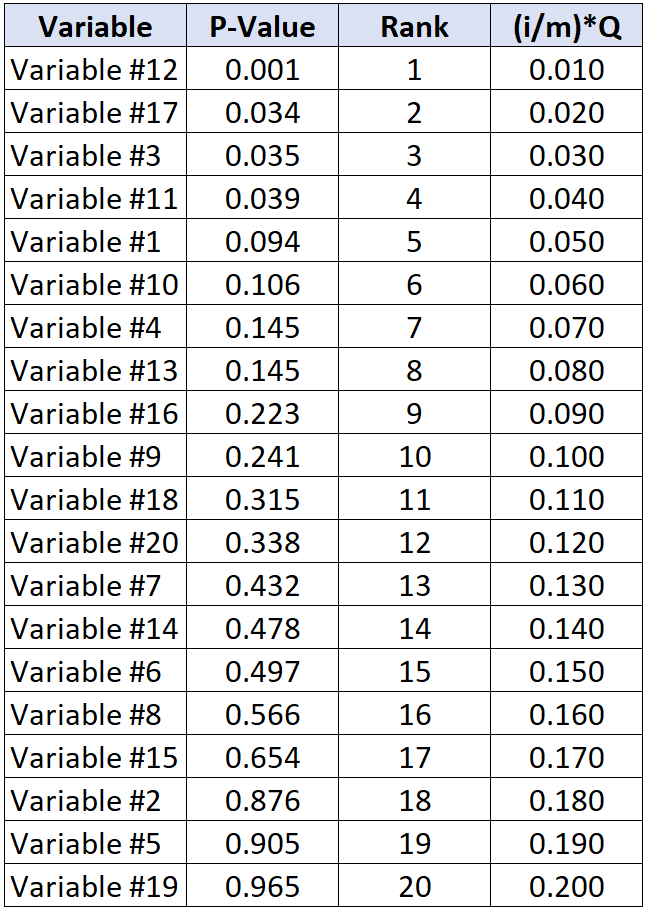
Критерий с наибольшим p-значением, которое меньше его критического значения Бенджамини-Хохберга, — это переменная № 11, которая имеет p-значение 0,039 и критическое значение BH 0,040.
Таким образом, этот тест и все тесты с меньшим p-значением будут считаться значимыми.
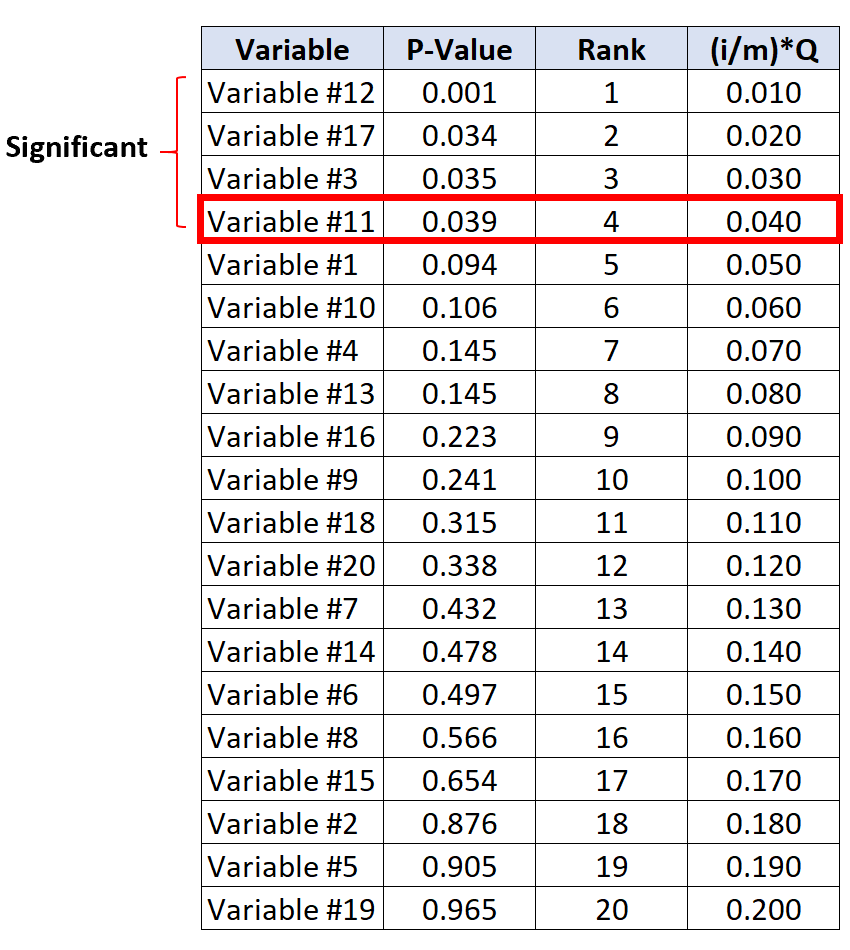
Обратите внимание, что хотя переменная № 17 и переменная № 3 не имели p-значения, которые были бы меньше их критических значений BH, они по-прежнему считаются значимыми, поскольку имеют меньшие p-значения, чем переменная № 11.
Как выбрать коэффициент ложного обнаружения
Одним из наиболее важных шагов в процедуре Бенджамини-Хохберга является выбор частоты ложных открытий. Вы должны выбрать частоту ложных открытий, прежде чем собирать какие-либо данные или проводить какие-либо статистические тесты.
Как правило, вы будете проводить большое количество статистических тестов на исследовательской фазе вашего анализа, после чего вы будете проводить дополнительные тесты для дальнейшего изучения ваших результатов.
Если последующие тесты недороги, вы можете рассмотреть возможность установки более высокого уровня ложных открытий, потому что даже если у вас будет несколько ложных открытий, вы, вероятно, обнаружите эти ложные открытия с помощью будущих тестов.
Кроме того, если цена пропущенного важного открытия высока, вы можете установить более высокую частоту ложных открытий, чтобы не пропустить ничего важного.
В зависимости от стоимости вашего исследования и важности не пропустить ни одного важного открытия, уровень ложных открытий будет варьироваться от одной ситуации к другой.
Дополнительные ресурсы
Объяснение P-значений и статистической значимости
Какова частота семейных ошибок?