Биномиальное распределение описывает вероятность достижения k успехов в n биномиальных экспериментах.
Если случайная величина X подчиняется биномиальному распределению, то вероятность того, что X = k успехов, можно найти по следующей формуле:
P(X=k) = n C k * p k * (1-p) nk
куда:
- n: количество испытаний
- k: количество успехов
- p: вероятность успеха в данном испытании
- n C k : количество способов добиться k успехов в n испытаниях.
Биномиальное распределение вероятностей имеет форму колокола, когда выполняется одно или несколько из следующих двух условий:
1. Размер выборки (n) большой.
2. Вероятность успеха в данном испытании (p) близка к 0,5.
Однако биномиальное распределение вероятностей имеет тенденцию к искажению, когда ни одно из этих условий не выполняется. Чтобы проиллюстрировать это, рассмотрим следующие примеры:
Пример 1. Размер выборки (n) большой
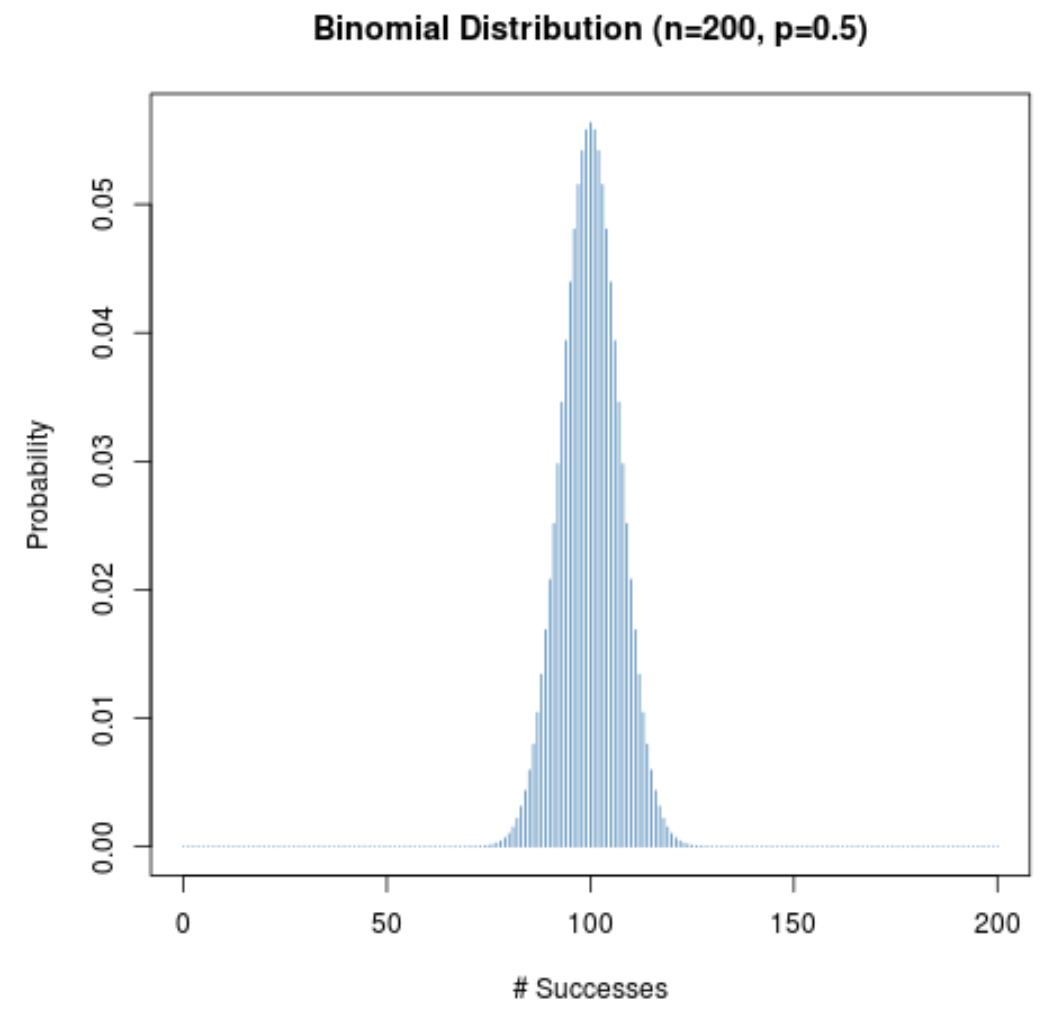
На следующей диаграмме показано распределение вероятностей при n = 200 и p = 0,5 .
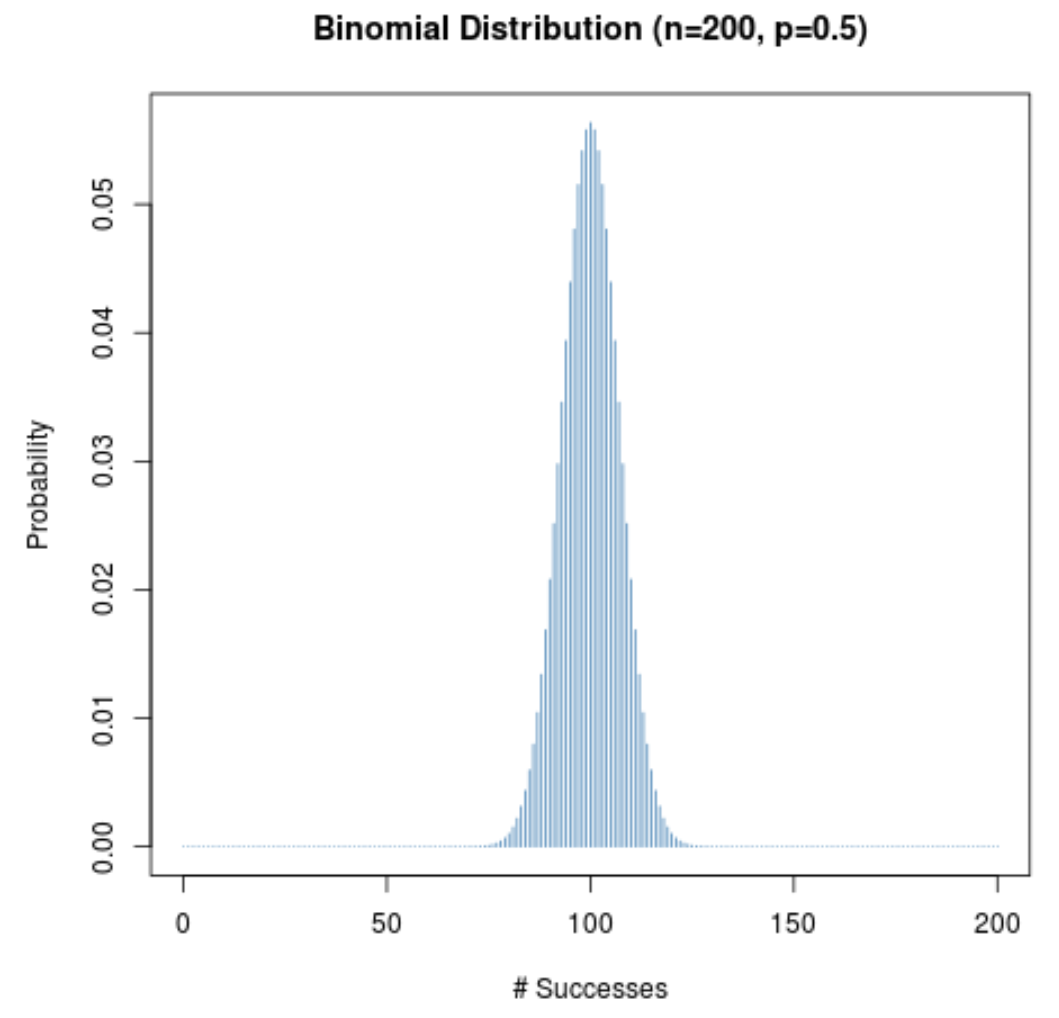
По оси X отображается количество успешных попыток за 200 попыток, а по оси Y — вероятность того, что произойдет это количество успешных попыток.
Поскольку (1) размер выборки велик и (2) вероятность успеха в данном испытании близка к 0,5, распределение вероятностей имеет колоколообразную форму.
Даже когда вероятность успеха в данном испытании (p) не близка к 0,5, распределение вероятностей все равно будет колоколообразным до тех пор, пока размер выборки (n) велик. Чтобы проиллюстрировать это, рассмотрим следующие два сценария, когда p = 0,2 и p = 0,8.
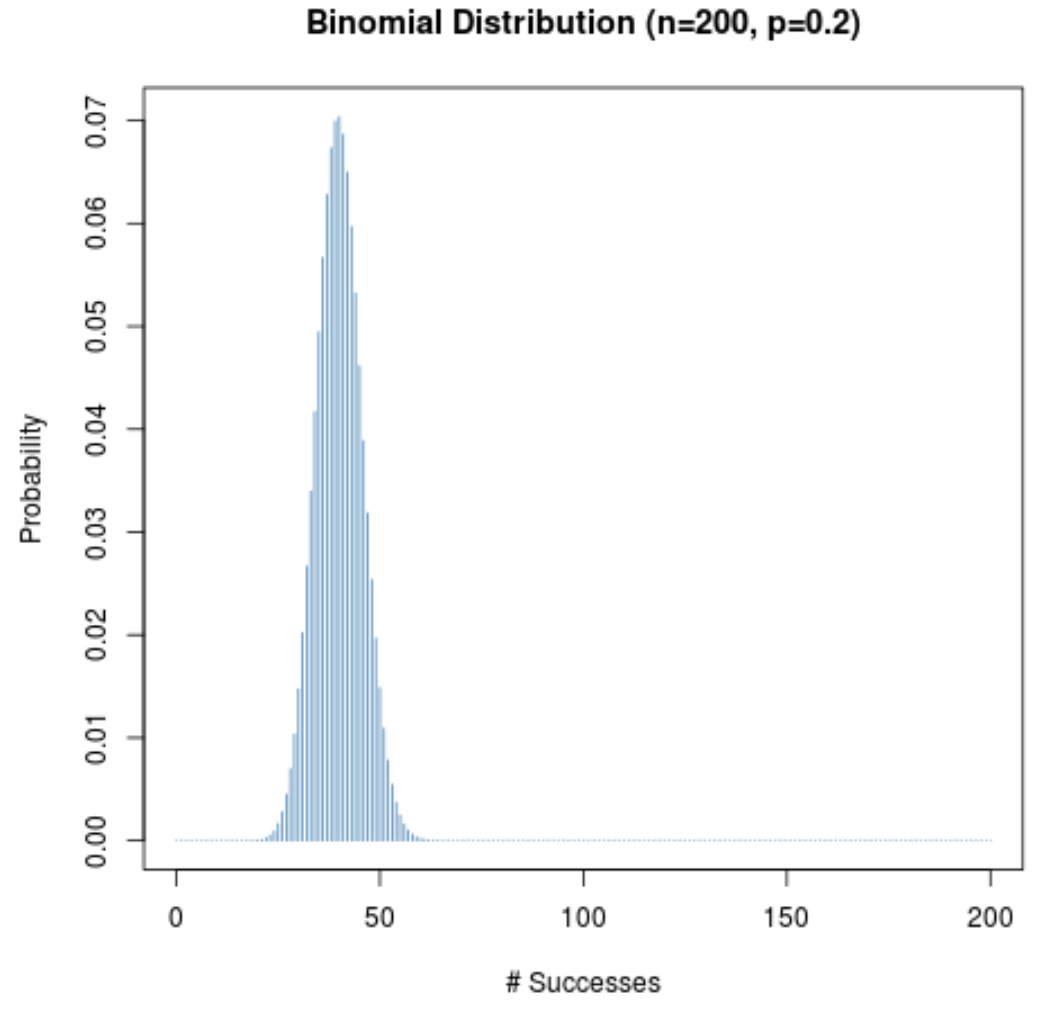
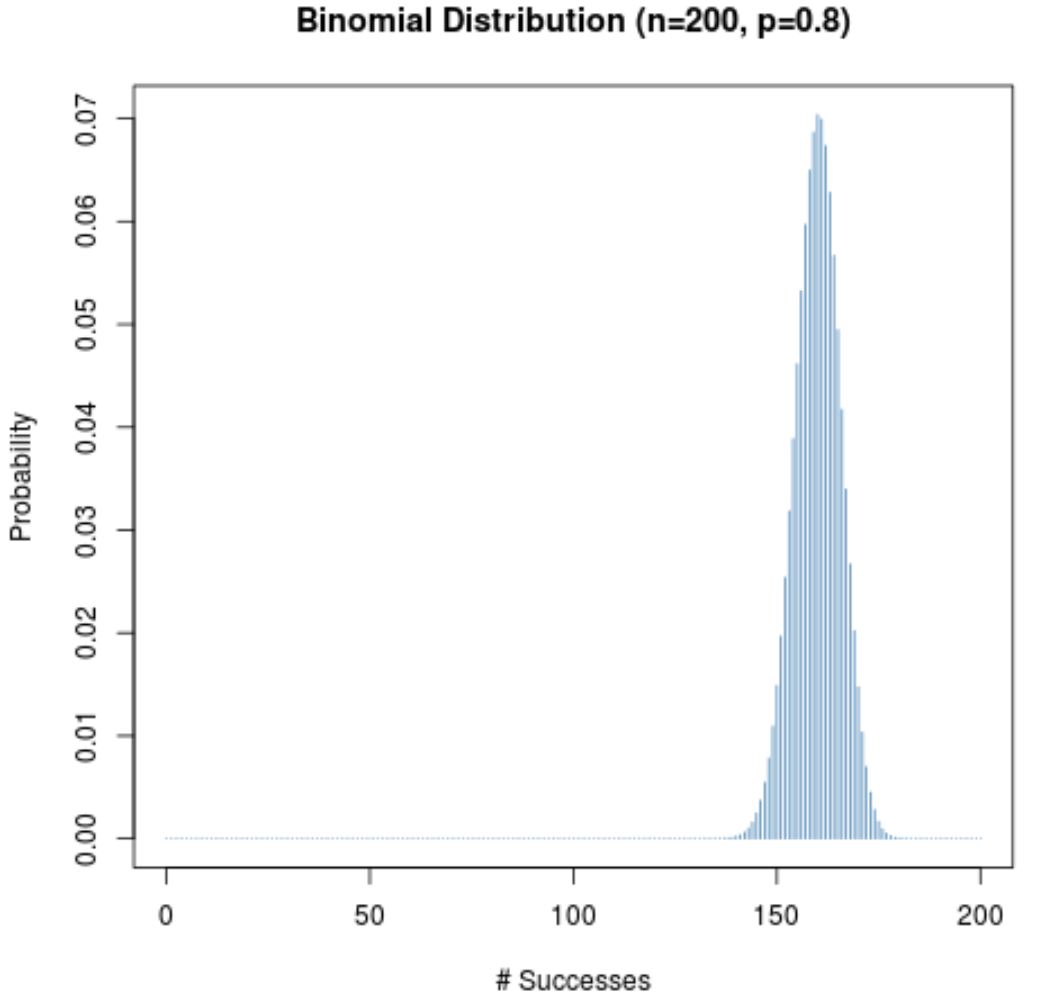
Обратите внимание на колоколообразную форму распределения вероятностей в обоих сценариях.
Пример 2: Вероятность успеха (p) близка к 0,5
На следующей диаграмме показано распределение вероятностей при n = 10 и p = 0,4 .
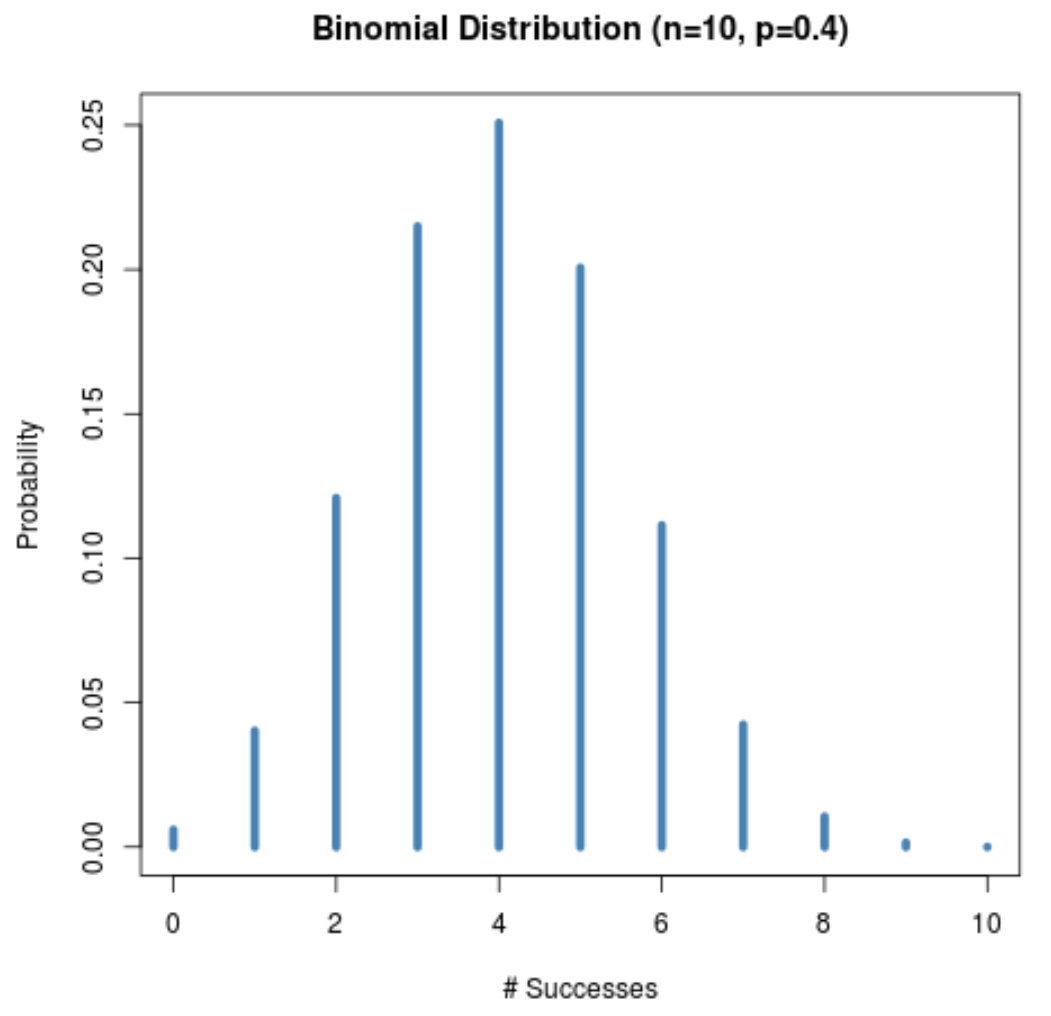
Хотя размер выборки (n = 10) невелик, распределение вероятностей по-прежнему имеет колоколообразную форму, поскольку вероятность успеха в данном испытании (p = 0,4) близка к 0,5.
Пример 3: асимметричные биномиальные распределения
Когда ни (1) размер выборки не велик, ни (2) вероятность успеха в данном испытании не близка к 0,5, биномиальное распределение вероятностей будет скошено влево или вправо.
Например, на следующем графике показано распределение вероятностей при n = 20 и p = 0,1 .
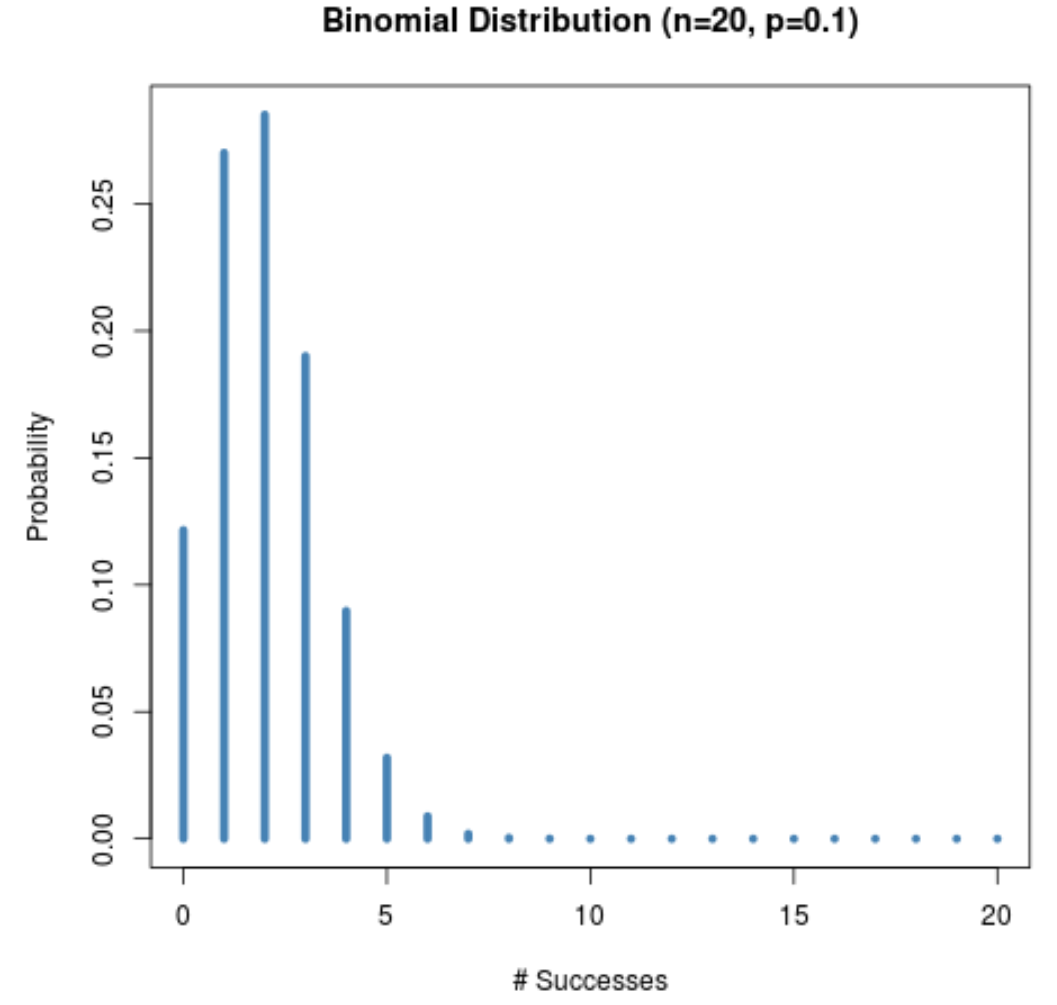
Обратите внимание, как распределение смещено вправо.
На следующем графике показано распределение вероятностей при n = 20 и p = 0,9 .
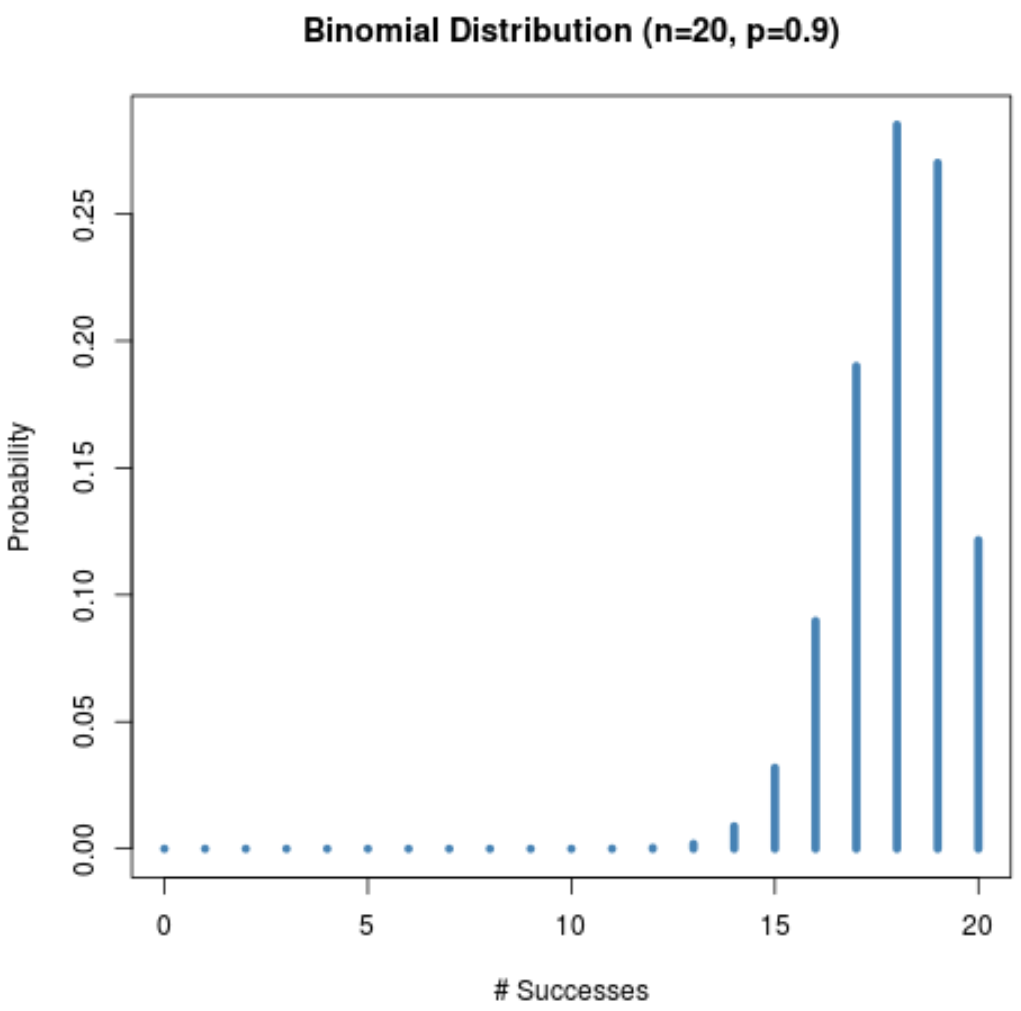
Обратите внимание, как распределение смещено влево.
Заключительные примечания
Каждая из диаграмм в этом посте была создана с использованием статистического языка программирования R. Узнайте, как построить собственное биномиальное распределение вероятностей в R с помощью этого руководства .