@import url('https://fonts.googleapis.com/css?family=Droid+Serif|Raleway');
words {
color: black; font-family: Raleway; max-width: 550px; margin: 25px auto; line-height: 1.75; padding-left: 100px; }
words label, input {
display: inline-block; vertical-align: baseline; width: 350px; }
#button { border: 1px solid; border-radius: 10px; margin-top: 20px; padding: 10px 10px; cursor: pointer; outline: none; background-color: white; color: black; font-family: 'Work Sans', sans-serif; border: 1px solid grey; /* Green */ }
#button:hover { background-color: #f6f6f6; border: 1px solid black; }
p, li { color:#000000; font-size: 19px; font-family: 'Helvetica'; }
p a { color: #9b59b6 !important; } Биномиальное распределение является одним из самых популярных распределений в статистике. Чтобы понять биномиальное распределение, сначала нужно понять биномиальные эксперименты .
Биномиальные эксперименты
Биномиальный эксперимент — это эксперимент, обладающий следующими свойствами:
- Эксперимент состоит из n повторных попыток.
- Каждое испытание имеет только два возможных исхода.
- Вероятность успеха, обозначаемая p , одинакова для каждого испытания.
- Каждое испытание является независимым.
Наиболее очевидным примером биномиального эксперимента является подбрасывание монеты. Например, предположим, что мы подбрасываем монету 10 раз. Это биномиальный эксперимент, поскольку он обладает следующими четырьмя свойствами:
- Эксперимент состоит из n повторных попыток – всего 10 попыток.
- В каждом испытании есть только два возможных исхода — орел или решка.
- Вероятность успеха, обозначаемая p , одинакова для каждого испытания. Если мы определим «успех» как приземление орлом, то вероятность успеха для каждого испытания равна ровно 0,5.
- Каждое испытание является независимым — результат одного подбрасывания монеты не влияет на результат любого другого подбрасывания монеты.
Биномиальное распределение
Биномиальное распределение описывает вероятность достижения k успехов в n биномиальных экспериментах.
Если случайная величина X подчиняется биномиальному распределению, то вероятность того, что X = k успехов, можно найти по следующей формуле:
P(X=k) = n C k * p k * (1-p) nk
куда:
- n: количество испытаний
- k: количество успехов
- p: вероятность успеха в данном испытании
- n C k : количество способов добиться k успехов в n испытаниях.
Например, предположим, что мы подбрасываем монету 3 раза. Мы можем использовать приведенную выше формулу, чтобы определить вероятность получения 0, 1, 2 и 3 решек во время этих 3 подбрасываний:
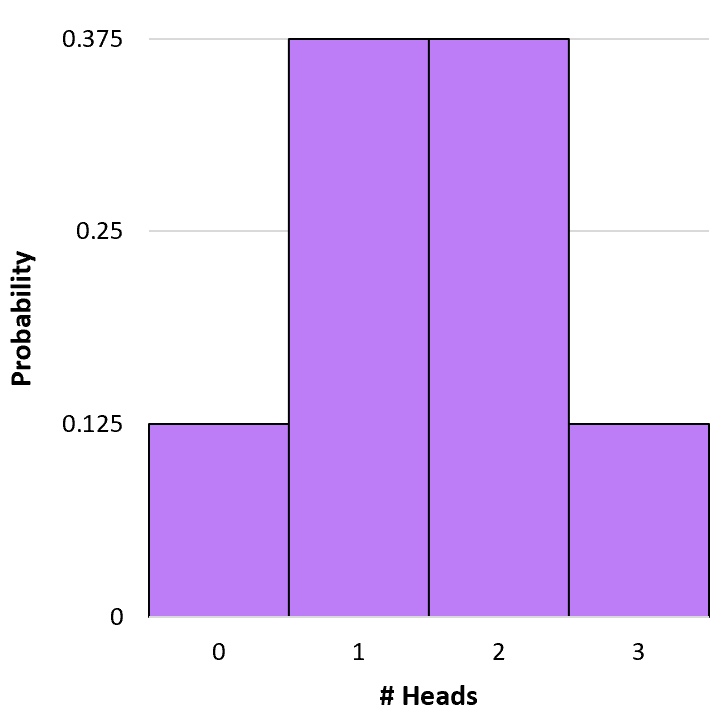
P(X=0) = 3 C 0 * 0,5 0 * (1-0,5) 3-0 = 1 * 1 * (0,5) 3 = 0,125
P(X=1) = 3 C 1 * 0,5 1 * (1-0,5) 3-1 = 3 * 0,5 * (0,5) 2 = 0,375
P(X=2) = 3 C 2 * 0,5 2 * (1-0,5) 3-2 = 3 * 0,25 * (0,5) 1 = 0,375
P(X=3) = 3 C 3 * 0,5 3 * (1-0,5) 3-3 = 1 * 0,125 * (0,5) 0 = 0,125
Примечание. Мы использовали этот Калькулятор комбинаций для расчета n C k для каждого примера.
Мы можем создать простую гистограмму, чтобы визуализировать это распределение вероятностей:
### Вычисление кумулятивных биномиальных вероятностей
Несложно рассчитать одну биномиальную вероятность (например, вероятность того, что монета выпадет орлом 1 раз из 3 бросков), используя приведенную выше формулу, но для расчета кумулятивных биномиальных вероятностей нам нужно сложить отдельные вероятности.
Например, предположим, что мы хотим узнать вероятность того, что монета выпадет орлом 1 или менее раз из 3 бросков. Мы будем использовать следующую формулу для расчета этой вероятности:
P(X≤1) = P(X=0) + P(X=1) = 0,125 + 0,375 = 0,5 .
Это известно как кумулятивная вероятность , потому что она включает в себя добавление более одной вероятности. Мы можем рассчитать кумулятивную вероятность выпадения k или меньше орлов для каждого исхода, используя аналогичную формулу:
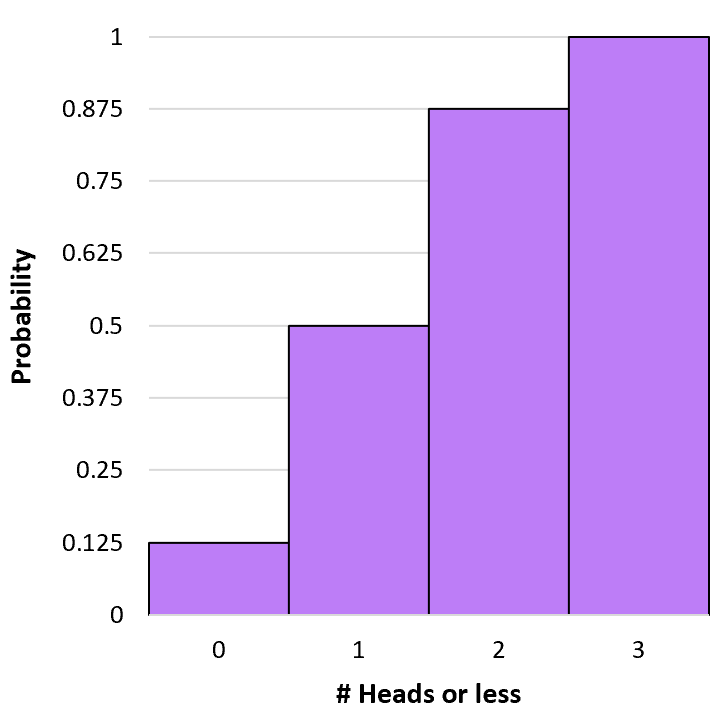
Р(Х≤0) = Р(Х=0) = 0,125 .
P(X≤1) = P(X=0) + P(X=1) = 0,125 + 0,375 = 0,5 .
P(X≤2) = P(X=0) + P(X=1) + P(X=2) = 0,125 + 0,375 + 0,375 = 0,875 .
P(X≤3) = P(X=0) + P(X=1) + P(X=2) + P(X=3) = 0,125 + 0,375 + 0,375 + 0,125 = 1 .
Мы можем создать гистограмму, чтобы визуализировать это кумулятивное распределение вероятностей:
### Калькулятор биномиальной вероятности
Когда мы работаем с небольшими числами (например, 3 подбрасывания монеты), целесообразно рассчитать биномиальные вероятности вручную. Однако, когда мы работаем с большими числами (например, 100 бросков монеты), вычисление вероятностей вручную может оказаться затруднительным. В этих случаях может быть полезно использовать калькулятор биномиальной вероятности , подобный приведенному ниже.
Например, предположим, что мы подбрасываем монету n = 100 раз, вероятность того, что она выпадет орлом в данном испытании, равна p = 0,5, и мы хотим узнать вероятность того, что она выпадет орлом k = 43 раза или меньше:
p (вероятность успеха в данном испытании) n (количество испытаний) k (количество успехов) Р(Х= 43 ) = 0,03007
Р(Х< 43 ) = 0,06661
Р( Х≤43 ) = 0,09667
Р(Х > 43 ) = 0,90333
Р( Х≥43 ) = 0,93339
function pvalue() {
//get input values var p = document.getElementById('p').value*1; var n = document.getElementById('n').value*1; var k = document.getElementById('k').value*1;
//assign probabilities to variable names var exactProb = jStat.binomial.pdf(k,n,p); var lessProb = jStat.binomial.cdf(k-1,n,p); var lessEProb = jStat.binomial.cdf(k,n,p); var greaterProb = 1-jStat.binomial.cdf(k,n,p); var greaterEProb = 1-jStat.binomial.cdf(k-1,n,p);
//output probabilities document.getElementById('k1').innerHTML = k; document.getElementById('k2').innerHTML = k; document.getElementById('k3').innerHTML = k; document.getElementById('k4').innerHTML = k; document.getElementById('k5').innerHTML = k;
document.getElementById('exactProb').innerHTML = exactProb.toFixed(5); document.getElementById('lessProb').innerHTML = lessProb.toFixed(5); document.getElementById('lessEProb').innerHTML = lessEProb.toFixed(5); document.getElementById('greaterProb').innerHTML = greaterProb.toFixed(5); document.getElementById('greaterEProb').innerHTML = greaterEProb.toFixed(5); } Вот как интерпретировать вывод:
- Вероятность того, что монета выпадет орлом ровно 43 раза, равна 0,03007 .
- Вероятность того, что монета выпадет орлом менее 43 раз, равна 0,06661 .
- Вероятность того, что монета выпадет орлом не более 43 раз, равна 0,09667 .
- Вероятность того, что монета выпадет орлом более 43 раз, равна 0,90333 .
- Вероятность того, что монета выпадет орлом 43 или более раз, равна 0,93339 .
Свойства биномиального распределения
Биномиальное распределение обладает следующими свойствами:
Среднее значение распределения равно µ = np
Дисперсия распределения равна σ 2 = np(1-p)
Стандартное отклонение распределения равно σ = √ np(1-p)
Например, предположим, что мы подбрасываем монету 3 раза. Пусть p = вероятность того, что монета выпадет орлом.
Среднее количество голов, которое мы ожидаем, равно μ = np = 3*.5 = 1.5 .
Ожидаемая дисперсия числа головок составляет σ 2 = np(1-p) = 3*,5*(1-,5) = 0,75 .
Проблемы практики биномиального распределения
Используйте следующие практические задачи, чтобы проверить свои знания о биномиальном распределении.
Проблема 1
Вопрос: Боб делает 60% своих штрафных бросков. Если он выполнит 12 штрафных бросков, какова вероятность того, что он сделает ровно 10?
Ответ: Используя приведенный выше калькулятор биномиального распределения с p = 0,6, n = 12 и k = 10, мы находим, что P(X=10) = 0,06385 .
Проблема 2
Вопрос: Джессика подбрасывает монету 5 раз. Какова вероятность того, что монета выпадет орлом 2 раза или меньше?
Ответ: Используя приведенный выше калькулятор биномиального распределения с p = 0,5, n = 5 и k = 2, мы находим, что P(X≤2) = 0,5 .
Проблема 3
Вопрос: Вероятность того, что данный студент будет принят в определенный колледж, равна 0,2. Если подали заявки 10 студентов, какова вероятность того, что будут приняты более 4?
Ответ: Используя приведенный выше калькулятор биномиального распределения с p = 0,2, n = 10 и k = 4, мы находим, что P(X>4) = 0,03279 .
Проблема 4
Вопрос: Вы подбрасываете монету 12 раз. Каково среднее ожидаемое количество выпавших орлов?
Ответ: Вспомните, что среднее биномиального распределения вычисляется как µ = np.Таким образом, µ = 12*0,5 = 6 голов .
Проблема 5
Вопрос: Марк совершает хоумран в 10% своих попыток. Если у него есть 5 попыток в данной игре, какова дисперсия количества хоум-ранов, которые он сделает?
Ответ: Напомним, что дисперсия биномиального распределения рассчитывается как σ 2 = np(1-p). Таким образом, σ 2 = 6*.1*(1-.1) = 0,54 .
Дополнительные ресурсы
Следующие статьи помогут вам научиться работать с биномиальным распределением в различных статистических программах: