Биномиальное распределение является одним из наиболее часто используемых распределений во всей статистике.
В калькуляторе TI-84 есть две функции, которые можно использовать для нахождения вероятностей, связанных с биномиальным распределением:
- binompdf(n, p, x) : находит вероятность того, что ровно x успехов произойдет во время n испытаний, где вероятность успеха в данном испытании равна p .
- binomcdf(n, p, x) : находит вероятность того, что x или меньше успешных результатов произойдет во время n испытаний, где вероятность успеха в данном испытании равна p .
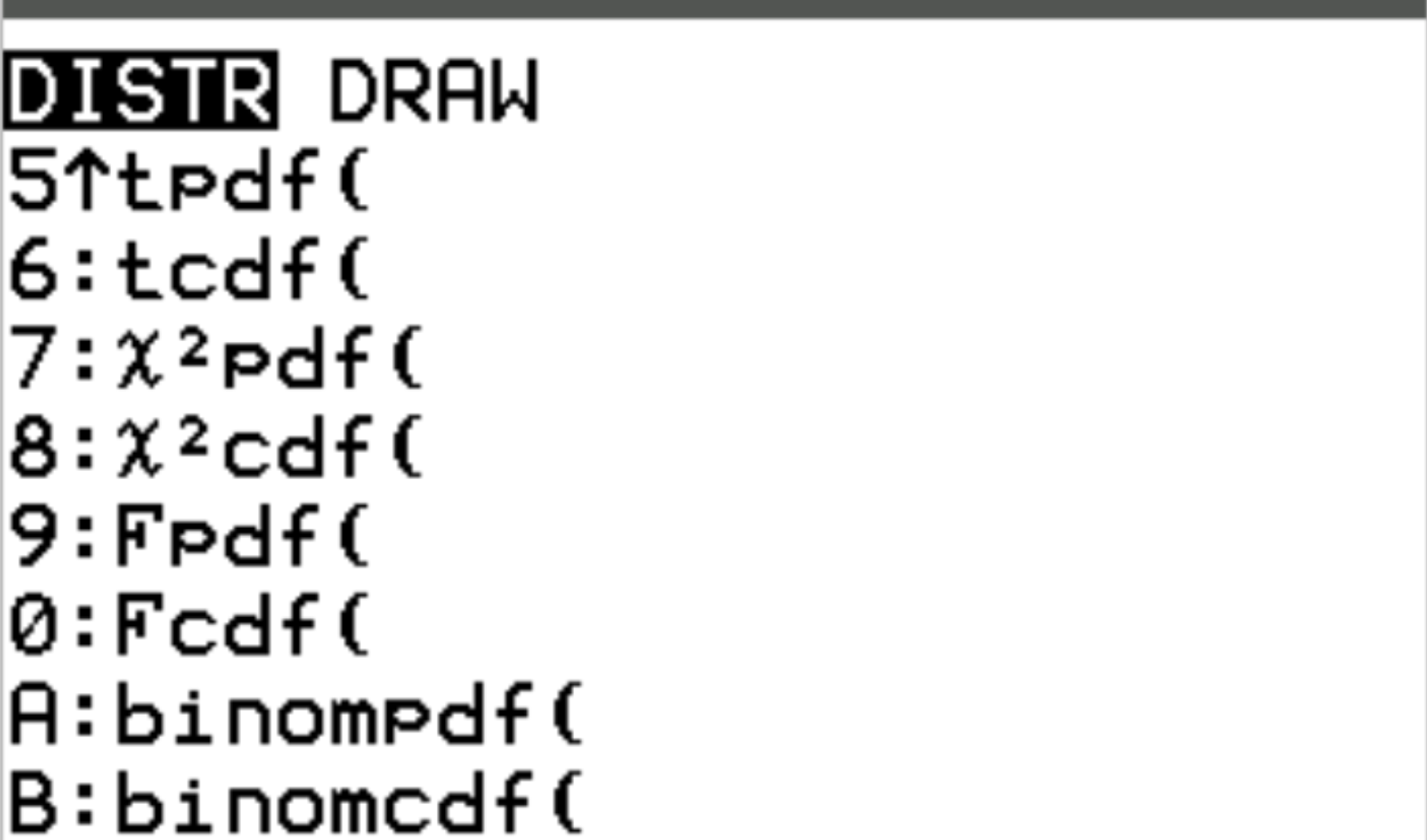
Вы можете получить доступ к каждой из этих функций на калькуляторе TI-84, нажав 2 -ю, а затем нажав VARS.Это приведет вас к экрану DISTR , где вы сможете использовать binompdf() и binomcdf() :
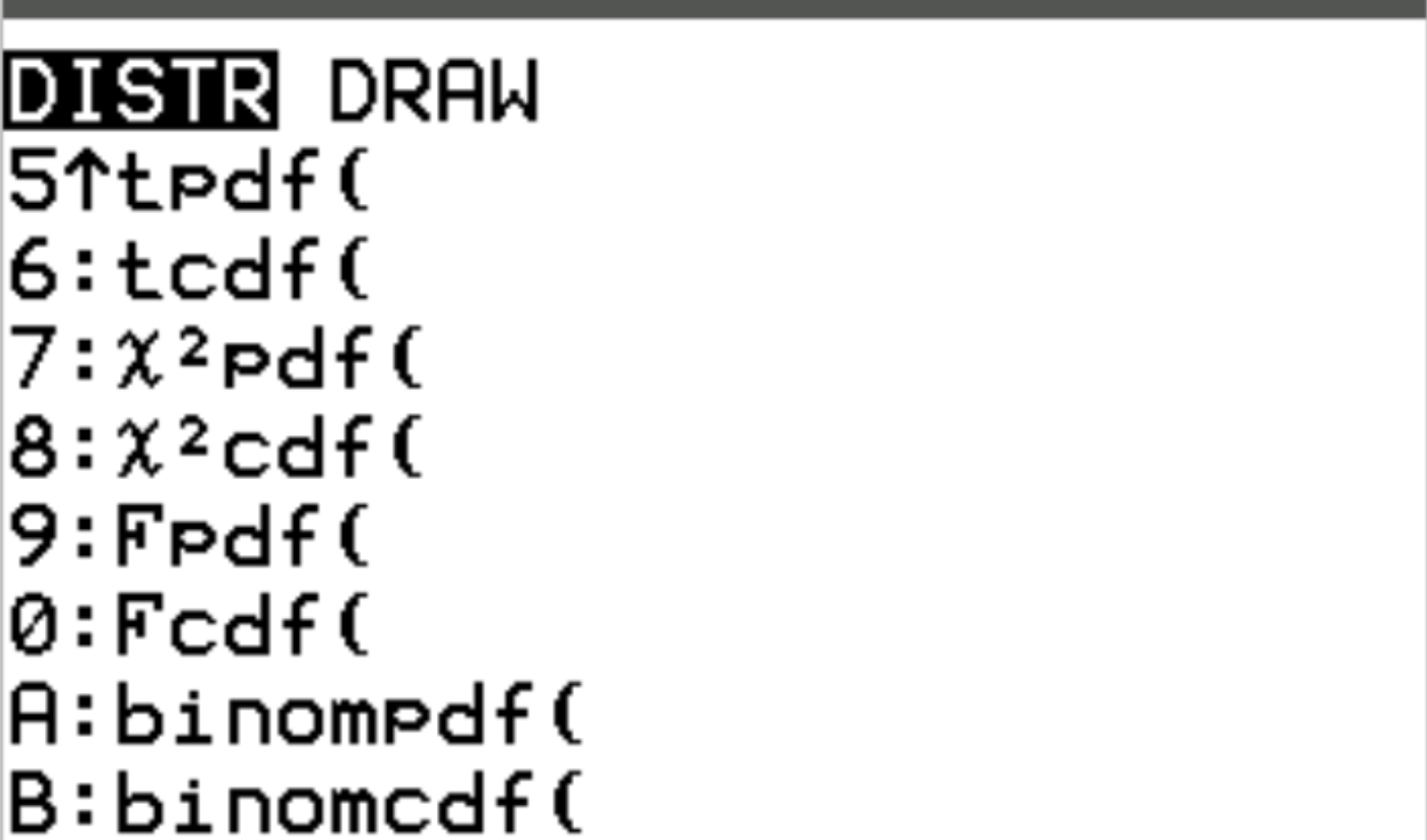
В следующих примерах показано, как использовать каждую из этих функций на практике.
Примеры: Как использовать Binompdf()
В следующих примерах показано, как использовать функцию binompdf() .
Пример 1: Попытки свободного броска
Джессика делает 80% своих штрафных бросков. Если она выполнит 10 штрафных бросков, какова вероятность того, что она сделает ровно 7?
Чтобы ответить на этот вопрос, мы можем ввести следующую формулу:

Вероятность того, что она сделает ровно 7, равна 0,2013 .
Пример 2: Мошеннические транзакции
Банк знает, что 3% всех транзакций являются мошенническими. Если в данный день происходит 20 транзакций, какова вероятность того, что ровно 2 из них будут мошенническими?
Чтобы ответить на этот вопрос, мы можем ввести следующую формулу:

Вероятность того, что ровно 2 транзакции являются мошенническими, равна 0,0988 .
Примеры: Как использовать Binomcdf()
В следующих примерах показано, как использовать функцию binomcdf() .
Пример 1: Попытки свободного броска
Джессика выполняет 50% своих штрафных бросков. Если она выполнит 10 штрафных бросков, какова вероятность того, что она сделает 7 или меньше?
Чтобы ответить на этот вопрос, мы можем ввести следующую формулу:

Вероятность того, что она сделает 7 или менее штрафных бросков, равна 0,9453 .
Пример 2: Мошеннические транзакции
Банк знает, что 3% всех транзакций являются мошенническими. Если в данный день происходит 20 транзакций, какова вероятность того, что более 2 транзакций являются мошенническими?
Чтобы ответить на этот вопрос, мы можем ввести следующую формулу:

Вероятность того, что более 2 транзакций являются мошенническими, равна 0,021 .
Дополнительные ресурсы
Калькулятор биномиального распределения
Как выполнить биномиальный тест в Excel