Начальная загрузка — это метод, который можно использовать для оценки стандартной ошибки любой статистики и получениядоверительного интервала для статистики.
Основной процесс начальной загрузки выглядит следующим образом:
- Возьмите k повторных выборок с заменой из заданного набора данных.
- Для каждой выборки рассчитайте интересующую вас статистику.
- Это приводит к k различным оценкам для данной статистики, которые затем можно использовать для вычисления стандартной ошибки статистики и создания доверительного интервала для статистики.
Мы можем выполнить загрузку в R, используя следующие функции из библиотеки загрузки :
- Создайте образцы начальной загрузки.
загрузка(данные, статистика, R, …)
куда:
- данные: вектор, матрица или фрейм данных.
- статистика: функция, которая создает статистику для начальной загрузки.
R: Количество реплик начальной загрузки
Создайте доверительный интервал с начальной загрузкой.
boot.ci(загрузочный объект, конфигурация, тип)
куда:
- bootobject: объект, возвращаемый функцией boot().
- conf: Доверительный интервал для расчета. По умолчанию 0,95.
- type: Тип доверительного интервала для расчета. Варианты включают «норма», «базовый», «шпилька», «процент», «bca» и «все» — по умолчанию «все».
В следующих примерах показано, как использовать эти функции на практике.
Пример 1. Начальная загрузка одной статистики
Следующий код показывает, как вычислить стандартную ошибку дляR-квадрата простой модели линейной регрессии:
set.seed(0)
library (boot)
#define function to calculate R-squared
rsq_function <- function (formula, data, indices) {
d <- data[indices,] #allows boot to select sample
fit <- lm(formula, data=d) #fit regression model
return (summary(fit)$r.square) #return R-squared of model
}
#perform bootstrapping with 2000 replications
reps <- boot(data=mtcars, statistic=rsq_function, R=2000, formula=mpg~disp)
#view results of boostrapping
reps
ORDINARY NONPARAMETRIC BOOTSTRAP
Call:
boot(data = mtcars, statistic = rsq_function, R = 2000, formula = mpg ~
disp)
Bootstrap Statistics :
original bias std. error
t1\* 0.7183433 0.002164339 0.06513426
По результатам мы видим:
- Предполагаемый R-квадрат для этой регрессионной модели равен 0,7183433 .
- Стандартная ошибка для этой оценки составляет 0,06513426 .
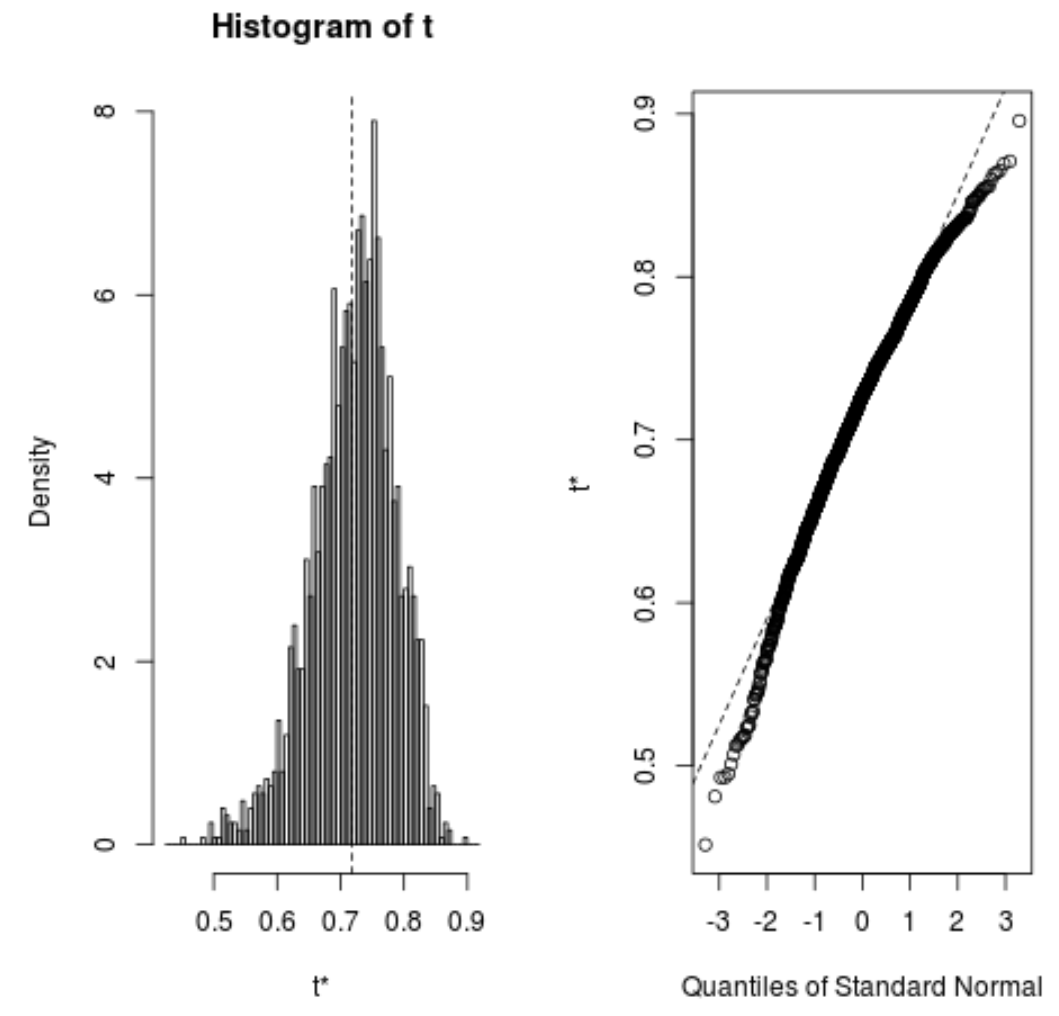
Мы также можем быстро просмотреть распределение загруженных образцов:
plot(reps)
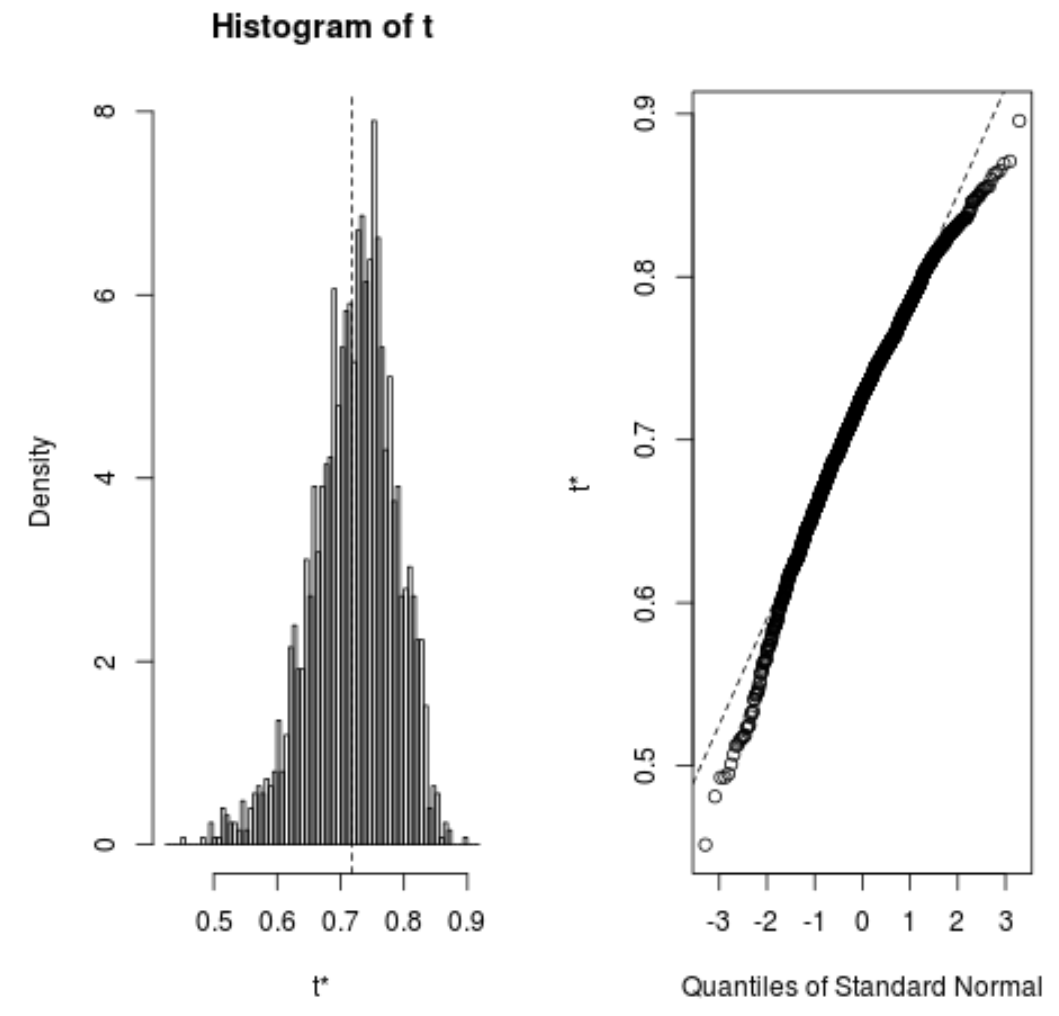
Мы также можем использовать следующий код для расчета 95% доверительного интервала для предполагаемого R-квадрата модели:
#calculate adjusted bootstrap percentile (BCa) interval
boot.ci(reps, type=" bca ")
CALL :
boot.ci(boot.out = reps, type = "bca")
Intervals :
Level BCa
95% ( 0.5350, 0.8188 )
Calculations and Intervals on Original Scale
Из вывода мы видим, что 95% доверительный интервал для истинных значений R-квадрата равен (0,5350, 0,8188).
Пример 2. Множественная статистика Bootstrap
Следующий код показывает, как вычислить стандартную ошибку для каждого коэффициента в модели множественной линейной регрессии:
set.seed(0)
library (boot)
#define function to calculate fitted regression coefficients
coef_function <- function (formula, data, indices) {
d <- data[indices,] #allows boot to select sample
fit <- lm(formula, data=d) #fit regression model
return (coef(fit)) #return coefficient estimates of model
}
#perform bootstrapping with 2000 replications
reps <- boot(data=mtcars, statistic=coef_function, R=2000, formula=mpg~disp)
#view results of boostrapping
reps
ORDINARY NONPARAMETRIC BOOTSTRAP
Call:
boot(data = mtcars, statistic = coef_function, R = 2000, formula = mpg ~
disp)
Bootstrap Statistics :
original bias std. error
t1\* 29.59985476 -5.058601e-02 1.49354577
t2\* -0.04121512 6.549384e-05 0.00527082
По результатам мы видим:
- Расчетный коэффициент для пересечения модели равен 29,59985476 , а стандартная ошибка этой оценки равна 1,49354577 .
- Предполагаемый коэффициент для предикторной переменной disp в модели равен -0,04121512 , а стандартная ошибка этой оценки равна 0,00527082 .
Мы также можем быстро просмотреть распределение загруженных образцов:
plot(reps, index=1) #intercept of model
plot(reps, index=2) #disp predictor variable
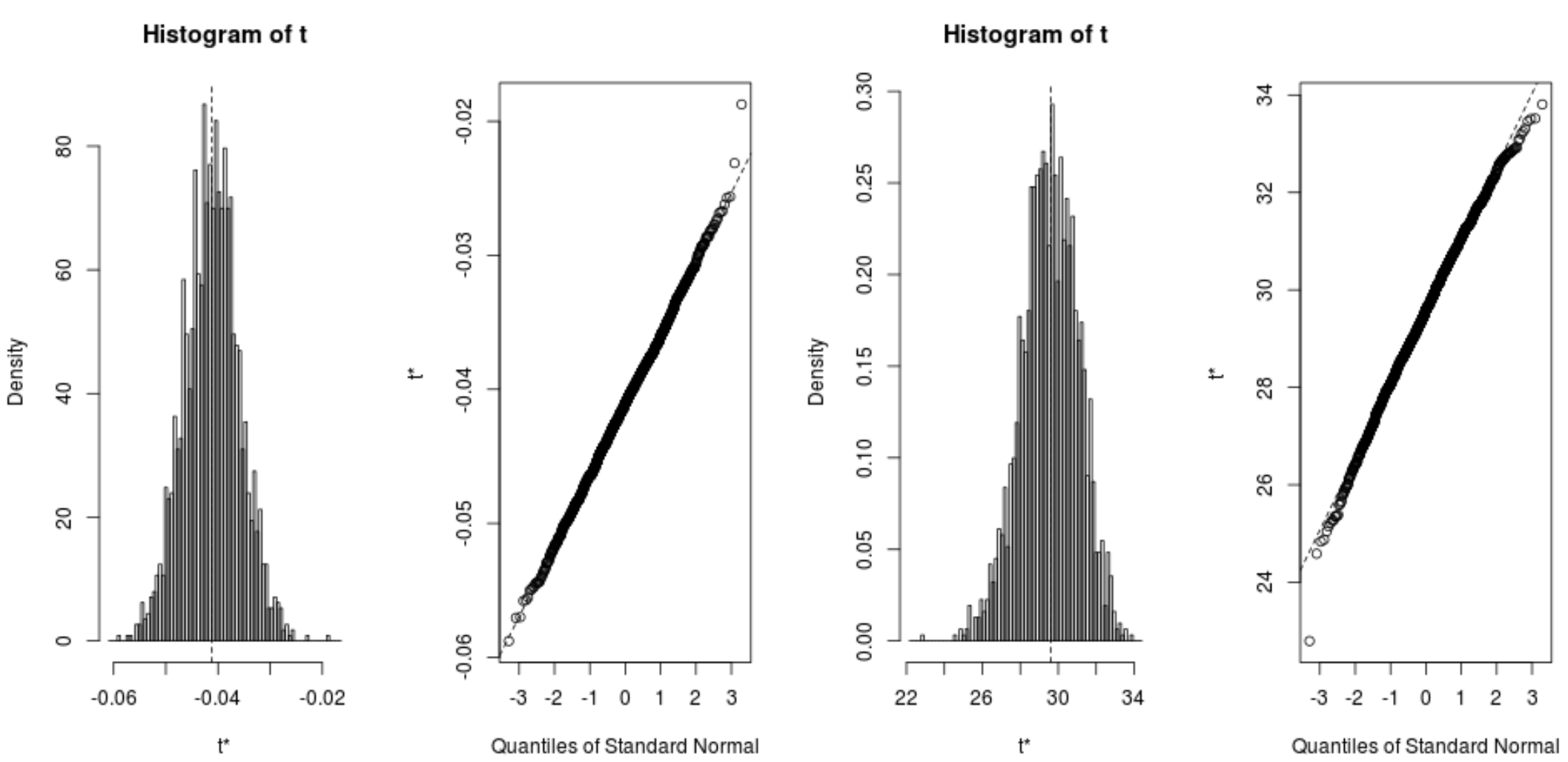
Мы также можем использовать следующий код для расчета 95% доверительных интервалов для каждого коэффициента:
#calculate adjusted bootstrap percentile (BCa) intervals
boot.ci(reps, type=" bca", index=1) #intercept of model
boot.ci(reps, type=" bca", index=2) #disp predictor variable
CALL :
boot.ci(boot.out = reps, type = "bca", index = 1)
Intervals :
Level BCa
95% (26.78, 32.66 )
Calculations and Intervals on Original Scale
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 2000 bootstrap replicates
CALL :
boot.ci(boot.out = reps, type = "bca", index = 2)
Intervals :
Level BCa
95% (-0.0520, -0.0312 )
Calculations and Intervals on Original Scale
Из вывода мы видим, что 95% доверительные интервалы с бутстрэпом для коэффициентов модели следующие:
- КИ для перехвата: (26,78, 32,66)
- CI для disp : (-.0520, -.0312)
Дополнительные ресурсы
Как выполнить простую линейную регрессию в R
Как выполнить множественную линейную регрессию в R
Введение в доверительные интервалы