Однофакторный дисперсионный анализ используется для определения того, существует ли значительная разница между средними значениями трех или более независимых групп.
Одно из предположений однофакторного дисперсионного анализа состоит в том, что дисперсии совокупностей, из которых взяты выборки , равны.
Один из наиболее распространенных способов проверить это — использовать тест Брауна-Форсайта , который представляет собой статистический тест, использующий следующие гипотезы :
- H 0 : Различия между популяциями равны.
- H A : Дисперсия между популяциями неодинакова.
Если p-значение теста меньше некоторого уровня значимости (например, α = 0,05), тогда мы отклоняем нулевую гипотезу и делаем вывод, что дисперсии не равны между различными популяциями.
В этом руководстве представлен пошаговый пример выполнения теста Брауна-Форсайта в R.
Шаг 1: введите данные
Предположим, мы хотим знать, приводят ли три разные программы тренировок к разным уровням потери веса.
Чтобы проверить это, мы набираем 90 человек и случайным образом назначаем 30 для использования каждой программы. Затем мы измеряем потерю веса каждого человека через месяц.
Следующий набор данных содержит информацию о том, сколько веса люди потеряли по каждой программе:
#make this example reproducible
set.seed(0)
#create data frame
data <- data.frame(program = as.factor ( rep (c(" A", " B", " C "), each = 30)),
weight_loss = c( runif (30, 0, 3),
runif (30, 0, 5),
runif (30, 1, 7)))
#view first six rows of data frame
head(data)
# program weight_loss
#1 A 2.6900916
#2 A 0.7965260
#3 A 1.1163717
#4 A 1.7185601
#5 A 2.7246234
#6 A 0.6050458
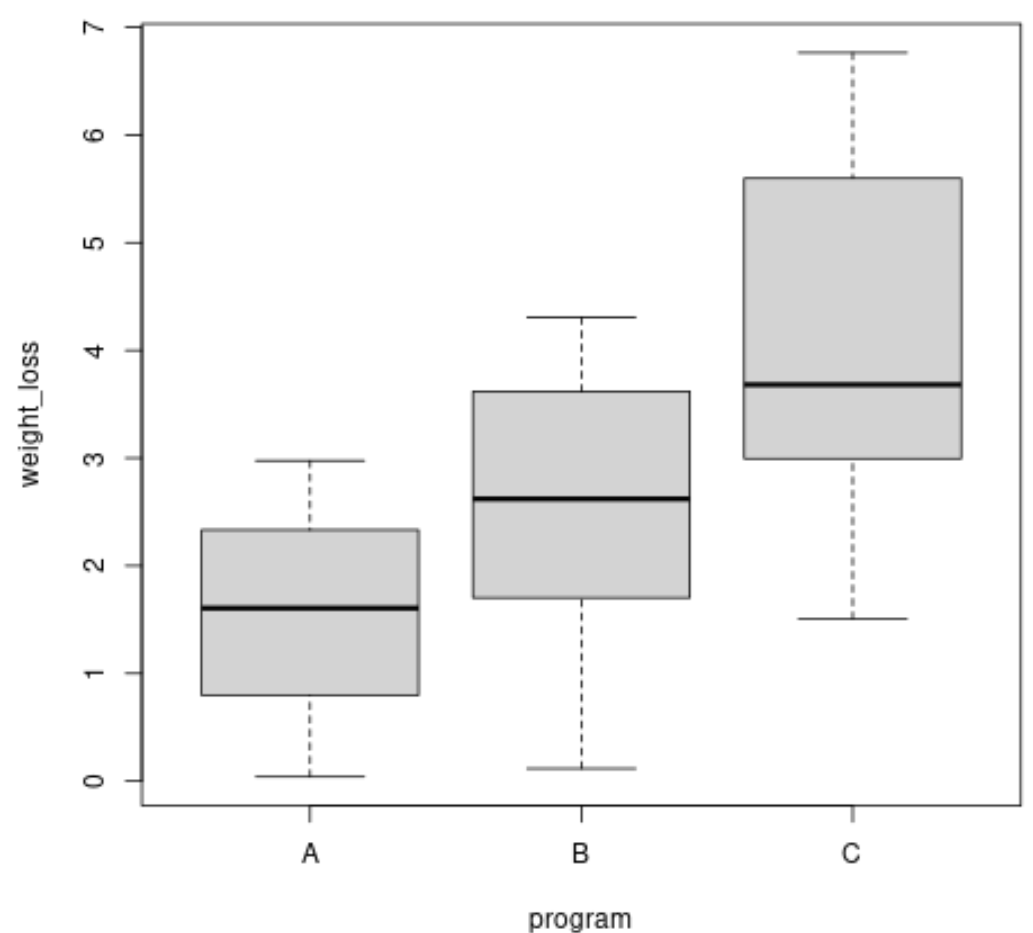
Шаг 2. Обобщите и визуализируйте данные
Прежде чем мы проведем тест Брауна-Форсайта, мы можем создать блок-диаграммы, чтобы визуализировать дисперсию потери веса для каждой группы:
boxplot(weight_loss ~ program, data = data)

Мы также можем рассчитать дисперсию потери веса в каждой группе:
#load dplyr package
library(dplyr)
#calculate variance of weight loss by group
data %>%
group_by(program) %>%
summarize(var=var(weight_loss))
# A tibble: 3 x 2
program var
1 A 0.819
2 B 1.53
3 C 2.46
Мы видим, что различия между группами различаются, но чтобы определить, являются ли эти различия статистически значимыми , мы можем выполнить тест Брауна-Форсайта.
Шаг 3. Проведите тест Брауна-Форсайта
Чтобы выполнить тест Брауна-Форсайта в R, мы можем использовать функцию bf.test() из пакета onewaytests :
#load onewaytests package
library (onewaytests)
#perform Brown-Forsythe test
bf.test(weight_loss ~ program, data = data)
Brown-Forsythe Test (alpha = 0.05)
-------------------------------------------------------------
data : weight_loss and program
statistic : 30.83304
num df : 2
denom df : 74.0272
p.value : 1.816529e-10
Result : Difference is statistically significant.
-------------------------------------------------------------
Значение p теста оказалось меньше 0,000, и, как показывают выходные данные, различия в дисперсиях между тремя группами статистически значимы.
Следующие шаги
Если вам не удалось отклонить нулевую гипотезу теста Брауна-Форсайта, вы можете приступить к однофакторному ANOVA для данных.
Однако, если вы отклоняете нулевую гипотезу, это означает, что предположение о равных дисперсиях нарушается. В этом случае у вас есть два варианта:
1. Все равно продолжите однофакторный дисперсионный анализ.
Оказывается, однофакторный дисперсионный анализ на самом деле устойчив к неравным дисперсиям, если наибольшая дисперсия не превышает наименьшую дисперсию более чем в 4 раза.
На шаге 2 из приведенного выше примера мы обнаружили, что наименьшая дисперсия составила 0,819, а наибольшая — 2,46. Таким образом, отношение наибольшей дисперсии к наименьшей равно 2,46/0,819 = 3,003 .
Поскольку это значение меньше 4, мы могли бы просто продолжить однофакторный дисперсионный анализ.
2. Проведите тест Крускала-Уоллиса
Если отношение наибольшей дисперсии к наименьшей дисперсии больше 4, мы можем вместо этого выбрать выполнение теста Краскела-Уоллиса.Это считается непараметрическим эквивалентом однофакторного дисперсионного анализа.
Пошаговый пример теста Крускала-Уоллиса в R можно найти здесь .