В статистике R-квадрат (R 2 ) измеряет долю дисперсии в переменной отклика , которая может быть объяснена предикторной переменной в регрессионной модели.
Мы используем следующую формулу для расчета R-квадрата:
R 2 = [ (nΣxy – (Σx)(Σy)) / (√ nΣx 2 -(Σx) 2 * √ nΣy 2 -(Σy) 2 ) ] 2
В следующем пошаговом примере показано, как рассчитать R-квадрат вручную для заданной модели регрессии.
Шаг 1: Создайте набор данных
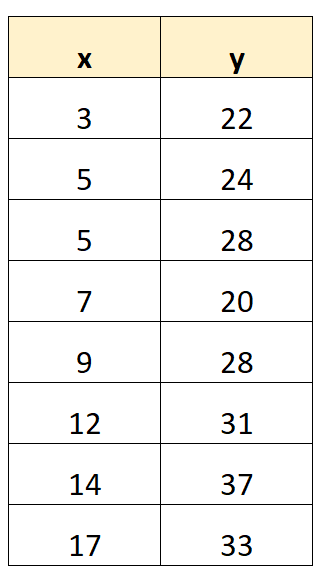
Во-первых, давайте создадим набор данных:

Шаг 2: Рассчитайте необходимые показатели
Далее давайте посчитаем каждую метрику, которую нам нужно использовать в формуле R 2 :

Шаг 3: Рассчитайте R-квадрат
Наконец, мы подставим каждую метрику в формулу для R 2 :
- R 2 = [ (nΣxy – (Σx)(Σy)) / (√ nΣx 2 -(Σx) 2 * √ nΣy 2 -(Σy) 2 ) ] 2
- R 2 = [ (8 * (2169) - (72) (223)) / (√ 8 * (818) - (72) 2 * √ 8 * (6447) - (223) 2 ) ] 2
- R 2 = 0,6686
Примечание.n в формуле представляет количество наблюдений в наборе данных и в этом примере оказывается n = 8 наблюдений.
Предполагая, что x является предикторной переменной, а y является переменной отклика в этой регрессионной модели, R-квадрат для модели равен 0,6686 .
Это говорит нам о том, что 66,86% вариации переменной y можно объяснить переменной x .
Дополнительные ресурсы
Введение в простую линейную регрессию
Введение в множественную линейную регрессию
R против R-Squared: в чем разница?
Что такое хорошее значение R-квадрата?