Одним из способов количественной оценки связи между двумя переменными является использованиекоэффициента корреляции Пирсона , который измеряет линейную связь между двумя переменными .
Он всегда принимает значение от -1 до 1, где:
- -1 указывает на совершенно отрицательную линейную корреляцию между двумя переменными
- 0 указывает на отсутствие линейной корреляции между двумя переменными
- 1 указывает на совершенно положительную линейную корреляцию между двумя переменными.
Чем дальше коэффициент корреляции от нуля, тем сильнее связь между двумя переменными.
В следующих примерах показано, как использовать proc corr в SAS для расчета коэффициента корреляции между переменными во встроенном наборе данных SAS под названием Fish , который содержит различные измерения для 159 различных рыб, пойманных в озере в Финляндии.
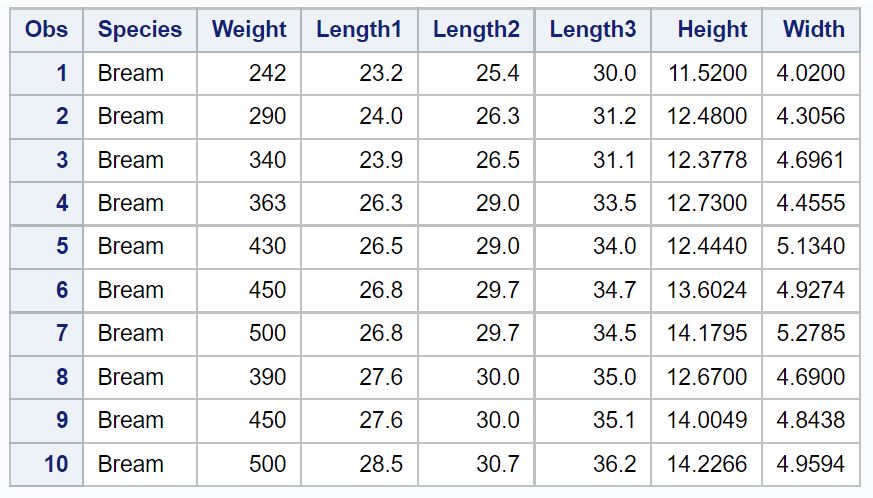
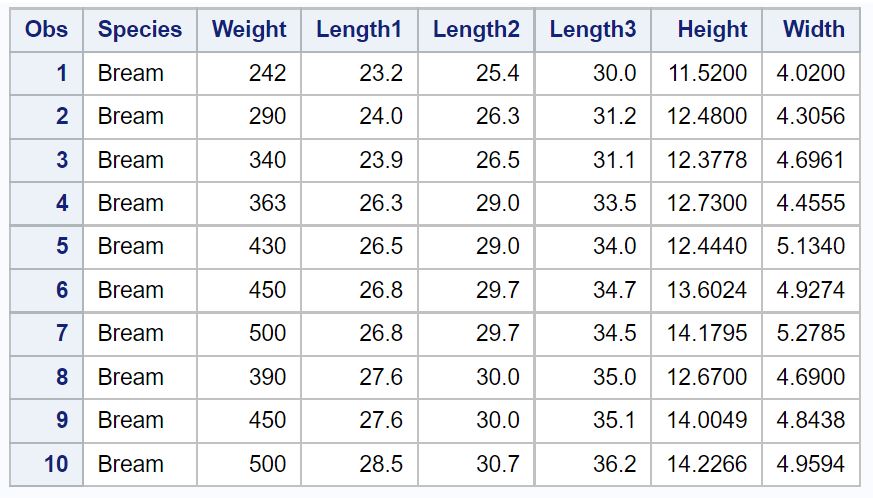
Мы можем использовать proc print для просмотра первых 10 наблюдений из этого набора данных:
/\*view first 10 observations from *Fish* dataset\*/
proc print data =sashelp.Fish ( obs = 10 );
run ;
Пример 1: Корреляция между двумя переменными
Мы можем использовать следующий код для вычисления коэффициента корреляции Пирсона между переменными Высота и Ширина:
/\*calculate correlation coefficient between Height and Width\*/
proc corr data =sashelp.fish;
var Height Width;
run ;
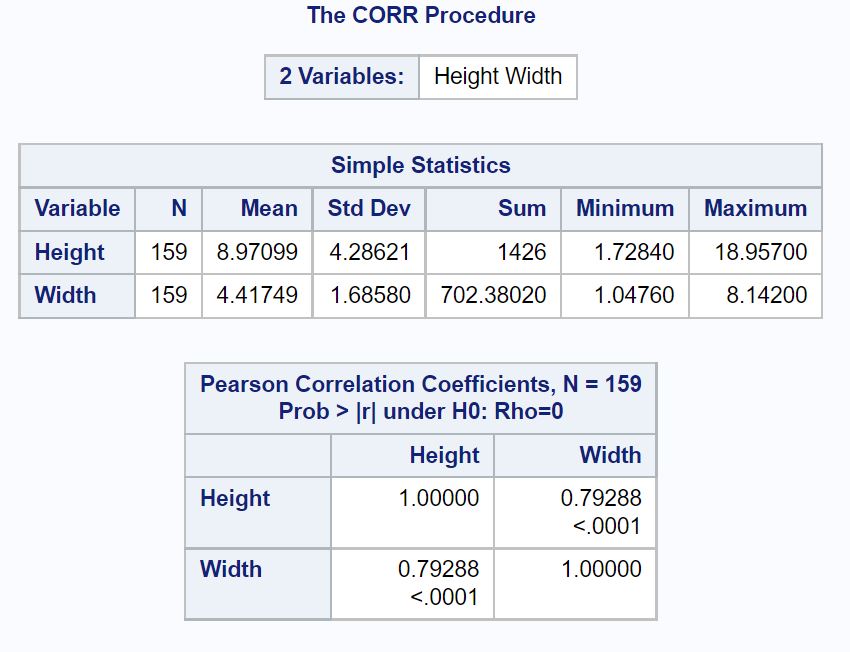
Первая таблица отображает сводную статистику как для высоты, так и для ширины.
Во второй таблице показан коэффициент корреляции Пирсона между двумя переменными, включая значение p , которое говорит нам, является ли корреляция статистически значимой.
Из вывода мы видим:
- Коэффициент корреляции Пирсона: 0,79288
- P-значение: <0,0001
Это говорит нам о наличии сильной положительной корреляции между высотой и шириной и о том, что корреляция является статистически значимой, поскольку значение p меньше α = 0,05.
По теме: Что считается «сильной» корреляцией?
Пример 2: Корреляция между всеми переменными
Мы можем использовать следующий код для вычисления коэффициента корреляции Пирсона между всеми парными комбинациями переменных в наборе данных:
/\*calculate correlation coefficient between all pairwise combinations of variables\*/
proc corr data =sashelp.fish;
run;
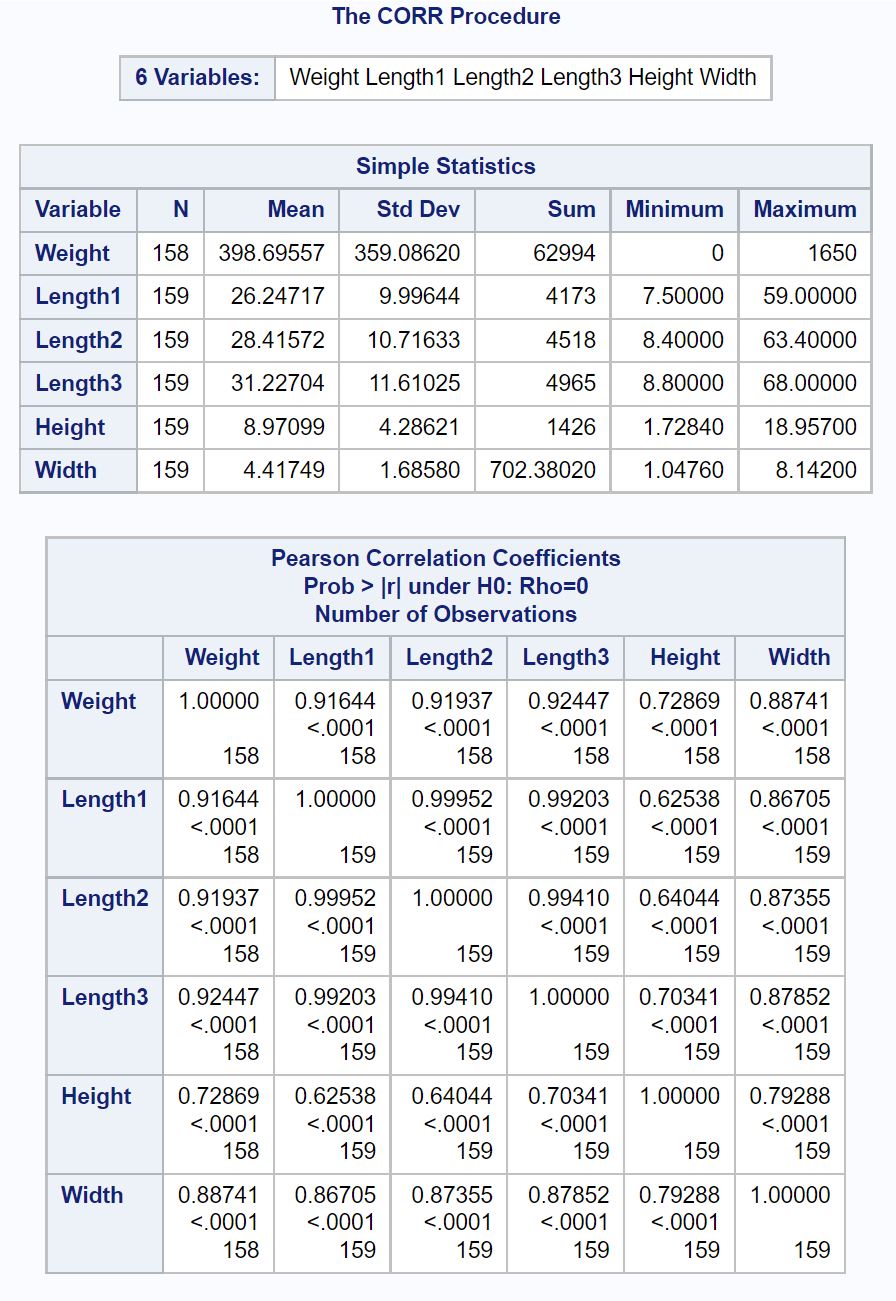
На выходе отображается матрица корреляции , которая содержит коэффициент корреляции Пирсона и соответствующие значения p для каждой попарной комбинации числовых переменных в наборе данных.
Например:
- Коэффициент корреляции Пирсона между весом и длиной1 составляет 0,91644.
- Коэффициент корреляции Пирсона между весом и длиной2 составляет 0,91937.
- Коэффициент корреляции Пирсона между весом и длиной3 составляет 0,92447.
И так далее.
Пример 3. Визуализация корреляции с помощью диаграммы рассеяния
Мы также можем использовать функцию plots для создания диаграммы рассеивания для визуализации корреляции между двумя переменными:
/\*visualize correlation between Height and Width\*/
proc corr data =sashelp.fish plots =scatter( nvar =all);;
var Height Width;
run;
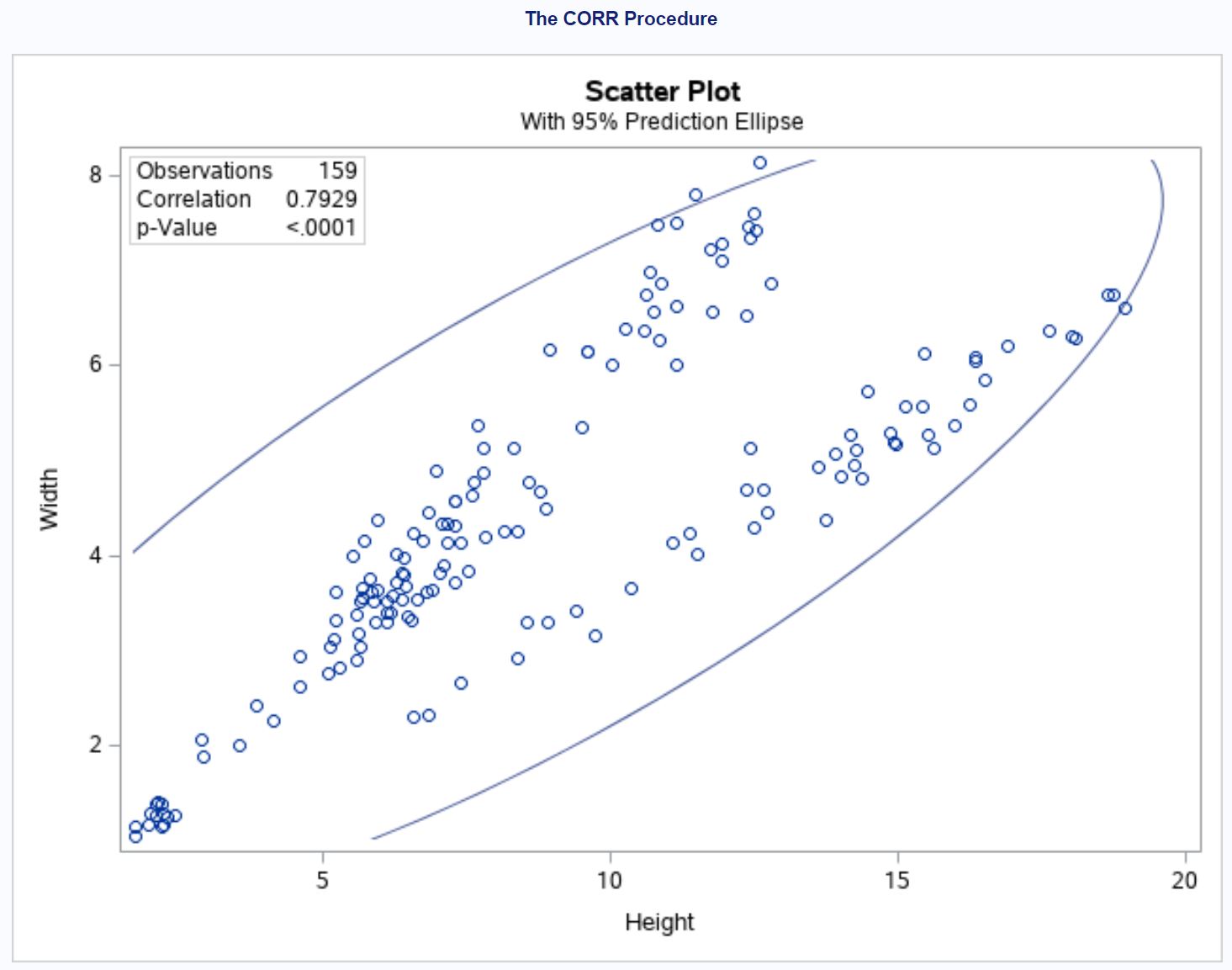
Из графика видно сильную положительную корреляцию между высотой и шириной. С увеличением высоты увеличивается и ширина.
В верхнем левом углу графика мы также можем видеть общее количество использованных наблюдений, коэффициент корреляции и значение p для коэффициента корреляции.
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные операции в SAS:
Как создать частотные таблицы в SAS
Как рассчитать описательную статистику в SAS