Часто вам может понадобиться подогнать кривую к некоторому набору данных в Python.

В следующем пошаговом примере объясняется, как подогнать кривые к данным в Python с помощью функции numpy.polyfit() и как определить, какая кривая лучше всего подходит к данным.
Шаг 1: Создайте и визуализируйте данные
Сначала давайте создадим поддельный набор данных, а затем создадим диаграмму рассеяния для визуализации данных:
import pandas as pd
import matplotlib.pyplot as plt
#create DataFrame
df = pd.DataFrame({'x': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15],
'y': [3, 14, 23, 25, 23, 15, 9, 5, 9, 13, 17, 24, 32, 36, 46]})
#create scatterplot of x vs. y
plt.scatter (df.x , df.y )

Шаг 2: Сопоставьте несколько кривых
Затем давайте подгоним несколько моделей полиномиальной регрессии к данным и визуализируем кривую каждой модели на одном графике:
import numpy as np
#fit polynomial models up to degree 5
model1 = np.poly1d (np.polyfit (df.x , df.y , 1))
model2 = np.poly1d (np.polyfit (df.x , df.y , 2))
model3 = np.poly1d (np.polyfit (df.x , df.y , 3))
model4 = np.poly1d (np.polyfit (df.x , df.y , 4))
model5 = np.poly1d (np.polyfit (df.x , df.y , 5))
#create scatterplot
polyline = np.linspace (1, 15, 50)
plt.scatter (df.x , df.y )
#add fitted polynomial lines to scatterplot
plt.plot (polyline, model1(polyline), color='green')
plt.plot (polyline, model2(polyline), color='red')
plt.plot (polyline, model3(polyline), color='purple')
plt.plot (polyline, model4(polyline), color='blue')
plt.plot (polyline, model5(polyline), color='orange')
plt.show()

Чтобы определить, какая кривая лучше всего соответствует данным, мы можем посмотреть на скорректированный R-квадрат каждой модели.
Это значение сообщает нам процентную долю вариации переменной отклика, которая может быть объяснена предикторной переменной (переменными) в модели с поправкой на количество предикторных переменных.
#define function to calculate adjusted r-squared
def adjR(x, y, degree):
results = {}
coeffs = np.polyfit (x, y, degree)
p = np.poly1d (coeffs)
yhat = p(x)
ybar = np.sum (y)/len(y)
ssreg = np.sum ((yhat-ybar)\*\*2)
sstot = np.sum ((y - ybar)\*\*2)
results['r_squared'] = 1- (((1-(ssreg/sstot))\*(len(y)-1))/(len(y)-degree-1))
return results
#calculated adjusted R-squared of each model
adjR(df.x , df.y , 1)
adjR(df.x , df.y , 2)
adjR(df.x , df.y , 3)
adjR(df.x , df.y , 4)
adjR(df.x , df.y , 5)
{'r_squared': 0.3144819}
{'r_squared': 0.5186706}
{'r_squared': 0.7842864}
{'r_squared': 0.9590276}
{'r_squared': 0.9549709}
Из вывода мы видим, что модель с самым высоким скорректированным R-квадратом является полиномом четвертой степени, у которого скорректированный R-квадрат равен 0,959 .
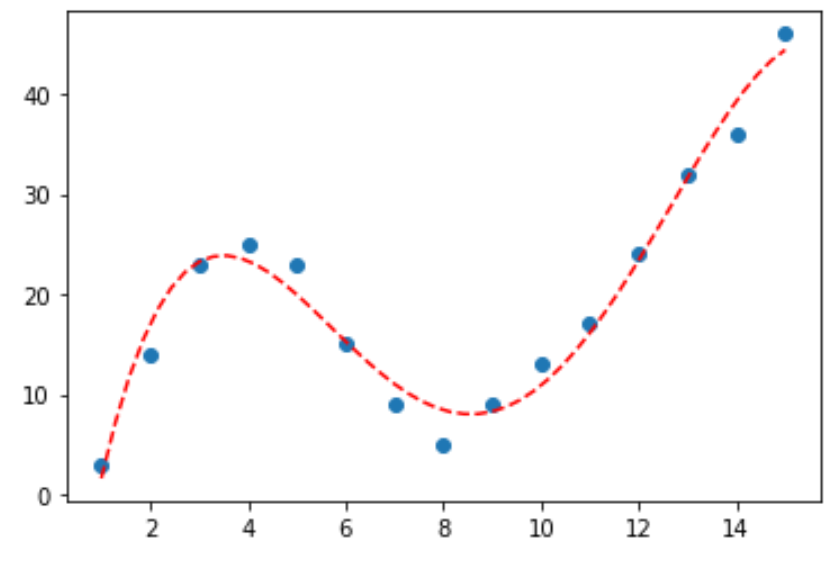
Шаг 3: Визуализируйте окончательную кривую
Наконец, мы можем создать диаграмму рассеяния с кривой полиномиальной модели четвертой степени:
#fit fourth-degree polynomial
model4 = np.poly1d (np.polyfit (df.x , df.y , 4))
#define scatterplot
polyline = np.linspace (1, 15, 50)
plt.scatter (df.x , df.y )
#add fitted polynomial curve to scatterplot
plt.plot (polyline, model4(polyline), '--', color='red')
plt.show()

Мы также можем получить уравнение для этой строки, используя функцию print() :
print(model4)
4 3 2
-0.01924 x + 0.7081 x - 8.365 x + 35.82 x - 26.52
Уравнение кривой выглядит следующим образом:
у = -0,01924 х 4 + 0,7081 х 3 – 8,365 х 2 + 35,82 х – 26,52
Мы можем использовать это уравнение для прогнозирования значения переменной отклика на основе переменных-предикторов в модели. Например, если x = 4, то мы можем предсказать, что y = 23,32 :
у = -0,0192(4) 4 + 0,7081(4) 3 – 8,365(4) 2 + 35,82(4) – 26,52 = 23,32
Дополнительные ресурсы
Введение в полиномиальную регрессию Как выполнить полиномиальную регрессию в Python