Временной ряд называется «стационарным», если он не имеет тренда, демонстрирует постоянную дисперсию во времени и имеет постоянную структуру автокорреляции во времени.
Один из способов проверить, является ли временной ряд стационарным, — это выполнить расширенный тест Дики-Фуллера , в котором используются следующие нулевая и альтернативная гипотезы:
H 0 : Временной ряд является нестационарным. Другими словами, он имеет некоторую структуру, зависящую от времени, и не имеет постоянной дисперсии во времени.
H A : временной ряд является стационарным.
Если p-значение из теста меньше некоторого уровня значимости (например, α = 0,05), то мы можем отвергнуть нулевую гипотезу и сделать вывод, что временной ряд является стационарным.
В следующем пошаговом примере показано, как выполнить расширенный тест Дики-Фуллера в Python для заданного временного ряда.
Пример: расширенный тест Дики-Фуллера в Python
Предположим, у нас есть следующие данные временного ряда в Python:
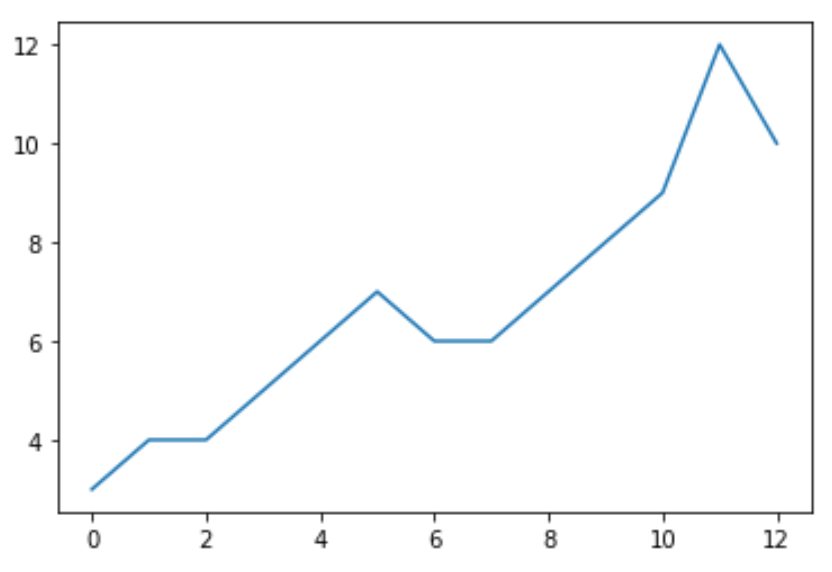
data = [3, 4, 4, 5, 6, 7, 6, 6, 7, 8, 9, 12, 10]
Прежде чем мы выполним расширенный тест Дики-Фуллера для данных, мы можем создать быстрый график для визуализации данных:
import matplotlib.pyplot as plt
plt.plot (data)
Чтобы выполнить расширенный тест Дики-Фуллера, мы можем использовать функцию adfuller() из библиотеки statsmodels.Во-первых, нам нужно установить statsmodels:
pip install statsmodels
Затем мы можем использовать следующий код для выполнения расширенного теста Дики-Фуллера:
from statsmodels. tsa.stattools import adfuller
#perform augmented Dickey-Fuller test
adfuller(data)
(-0.9753836234744063,
0.7621363564361013,
0,
12,
{'1%': -4.137829282407408,
'5%': -3.1549724074074077,
'10%': -2.7144769444444443},
31.2466098872313)
Вот как интерпретировать наиболее важные значения в выводе:
- Статистика теста: -0,97538
- P-значение: 0,7621
Поскольку p-значение не меньше 0,05, мы не можем отвергнуть нулевую гипотезу.
Это означает, что временной ряд является нестационарным. Другими словами, он имеет некоторую структуру, зависящую от времени, и не имеет постоянной дисперсии во времени.
Дополнительные ресурсы
Как построить временной ряд в Matplotlib
Как построить несколько рядов из фрейма данных Pandas
Как выполнить тест тренда Манна-Кендалла в Python