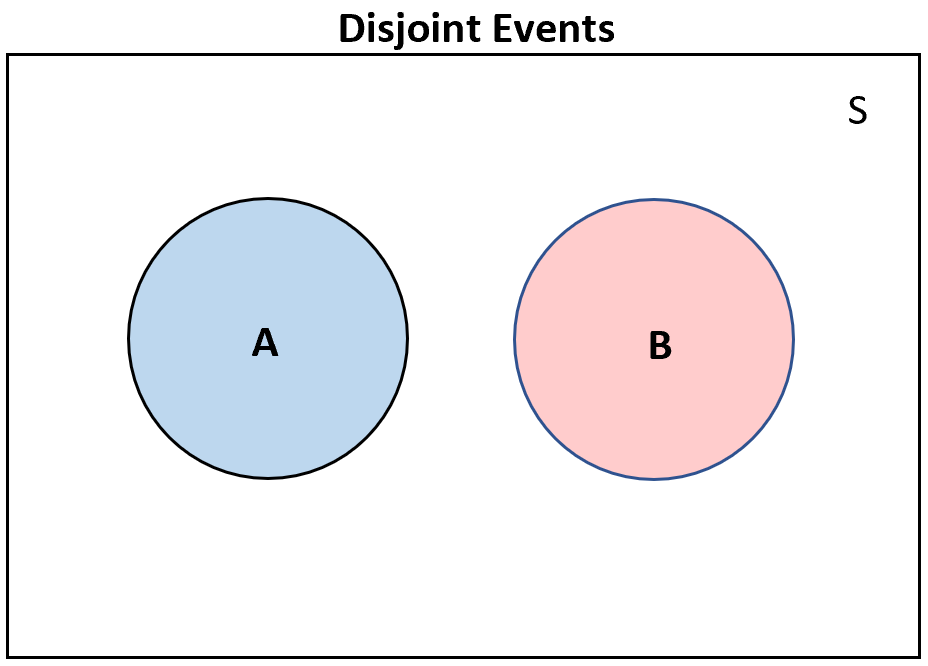
Непересекающиеся события — это события, которые не могут произойти одновременно.
Записанные в вероятностной нотации, события A и B не пересекаются, если их пересечение равно нулю. Это можно записать как:
- Р (А и В) = 0
- Р(А∩В) = 0
Например, предположим, что мы выбираем случайную карту из колоды. Пусть событие A будет событием, когда карта является пикой или трефой, а событие B будет событием, когда карта является червовой или бубновой.
Мы бы определили выборочное пространство для событий следующим образом:
- A = {пика, трефа}
- B = {Сердце, Алмаз}
Обратите внимание, что между двумя примерными пространствами нет перекрытия. Таким образом, события А и В являются непересекающимися событиями, поскольку они не могут произойти одновременно.
Примечание. Непересекающиеся события также называются взаимоисключающими .
Примеры непересекающихся событий
Вот еще несколько примеров непересекающихся событий.
Пример 1: Подбрасывание монеты
Предположим, вы подбрасываете монету. Пусть событие A — это событие, когда монета падает орлом, а событие B — это событие, когда монета падает решкой.
Событие А и событие В не пересекаются, потому что они не могут произойти одновременно. Монета не может упасть орлом и решкой.
Пример 2: Бросок костей
Предположим, вы бросаете кости. Пусть событие A — это событие, когда игральная кость выпадает на нечетное число, а событие B — это событие, когда игральная кость выпадает на четное число.
Событие А и событие В не пересекаются, потому что они не могут произойти одновременно. Кости не могут выпасть ни на четное, ни на нечетное число.
Пример 3: Местоположение Pro Bowl
Предположим, НФЛ хочет выбрать место для проведения Pro Bowl. Они сузили варианты до Майами и Сан-Диего. Они помещают оба имени в шляпу и случайным образом выбирают одно из них. Пусть событие A будет событием, когда они выберут Майами, а событием B будет событие, когда они выберут Сан-Диего.
Событие А и событие В не пересекаются, потому что они не могут произойти одновременно. Майами и Сан-Диего нельзя выбрать одновременно.
Визуализация непересекающихся событий
Одним из полезных способов визуализации непересекающихся событий является создание диаграммы Венна.
Если два события не пересекаются , то они вообще не будут пересекаться на диаграмме Венна:
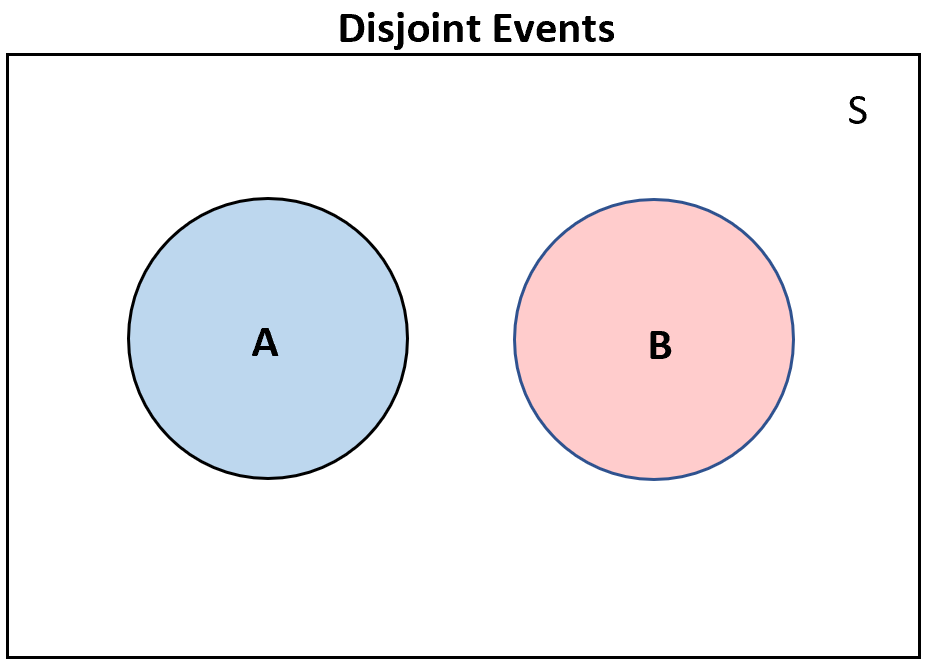
И наоборот, если два события не пересекаются , то на диаграмме Венна будет хотя бы некоторое перекрытие:
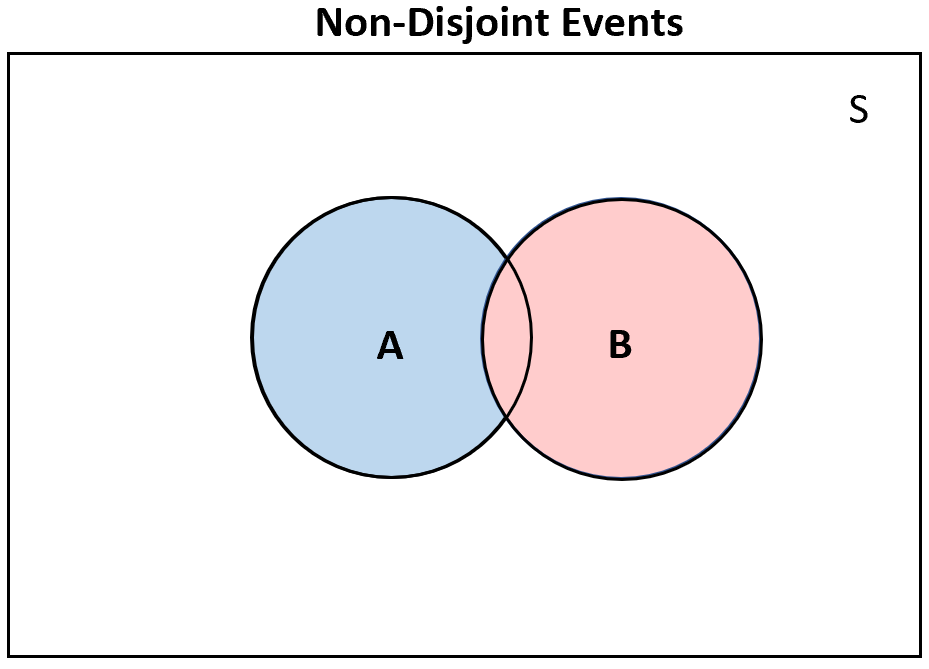
Вероятность непересекающихся событий
Как упоминалось ранее, если два события не пересекаются, то вероятность того, что они оба произойдут одновременно, равна нулю.
- Р(А∩В) = 0
Точно так же вероятность того, что любое событие произойдет, может быть рассчитана путем сложения их индивидуальных вероятностей.
- Р(А∪В) = Р(А) + Р(В)
Например, пусть событие А — это событие, когда игральная кость выпадает на 1 или 2, а событие В — это событие, когда игральная кость выпадает на 5 или 6.
Мы бы определили выборочное пространство для событий следующим образом:
- А = {1, 2}
- В = {5, 6}
Мы рассчитали бы вероятность события A или события B как:
- Р(А∪В) = Р(А) + Р(В)
- Р(А∪В) = 2/6 + 2/6
- Р(А∪В) = 4/6 = 2/3
Вероятность того, что произойдет событие А или событие В, равна 2/3 .
Дополнительные ресурсы
В следующих руководствах даются пояснения по другим распространенным темам, связанным с вероятностью:
Как найти вероятность A или B (с примерами)
Как найти вероятность A и B (с примерами)
Закон полной вероятности: определение и примеры