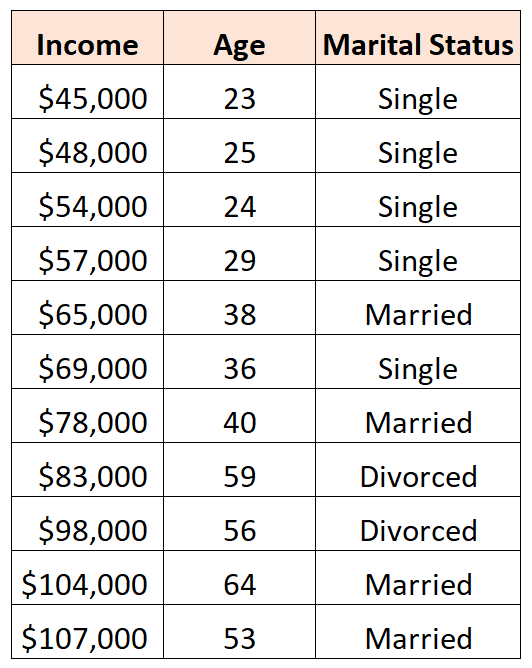
Фиктивная переменная — это тип переменной, которую мы создаем в регрессионном анализе, чтобы мы могли представить категориальную переменную как числовую переменную, которая принимает одно из двух значений: ноль или единицу.
Например, предположим, что у нас есть следующий набор данных, и мы хотели бы использовать возраст и семейное положение для прогнозирования дохода :
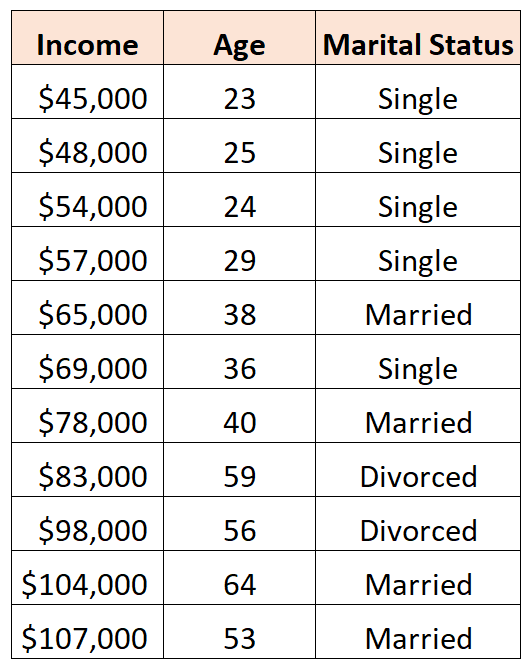
Чтобы использовать семейное положение в качестве предиктора в регрессионной модели, мы должны преобразовать его в фиктивную переменную.
Поскольку в настоящее время это категориальная переменная, которая может принимать три разных значения («Холост», «Женат» или «Разведен»), нам нужно создать k -1 = 3-1 = 2 фиктивных переменных.
Чтобы создать эту фиктивную переменную, мы можем позволить «Single» быть нашим базовым значением, поскольку оно встречается чаще всего. Вот как мы можем преобразовать семейное положение в фиктивные переменные:
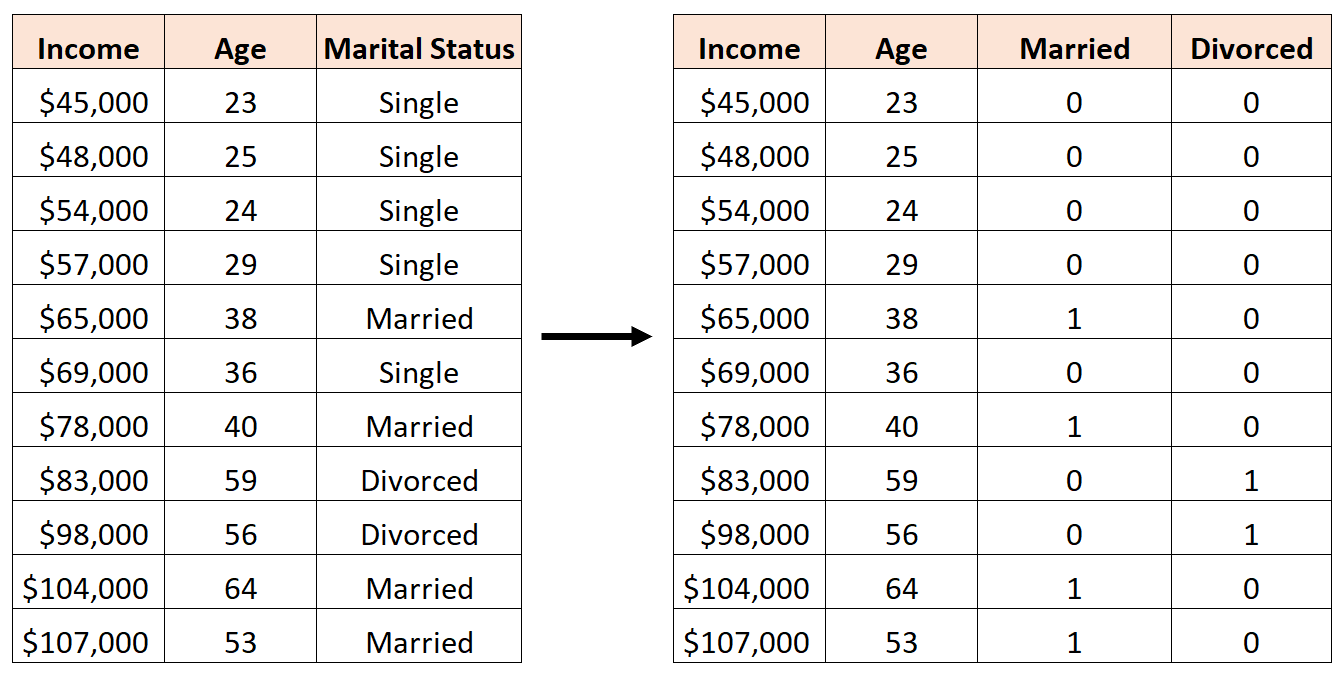
В этом руководстве представлен пошаговый пример того, как создать фиктивные переменные для этого точного набора данных в Excel, а затем выполнить регрессионный анализ, используя эти фиктивные переменные в качестве предикторов.
Шаг 1: Создайте данные
Сначала создадим набор данных в Excel:
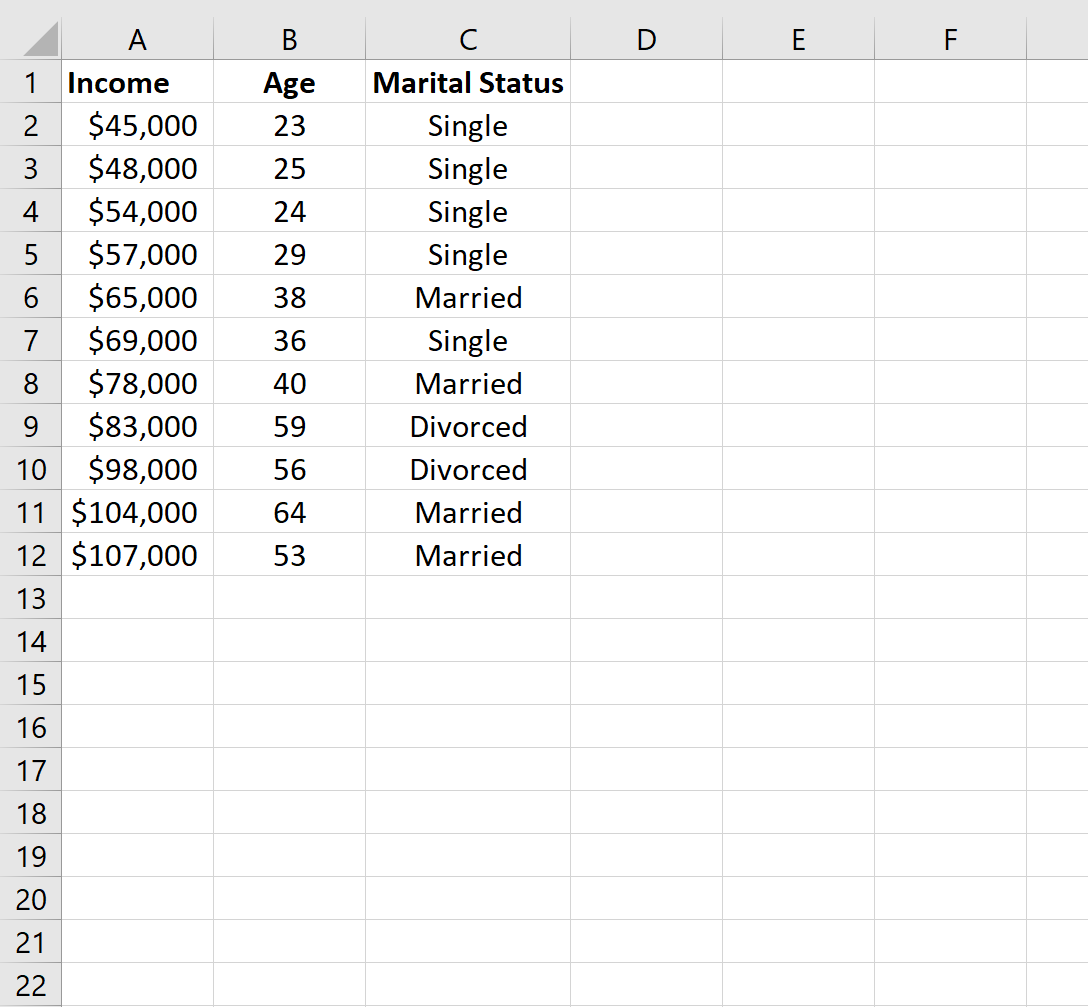
Шаг 2: Создайте фиктивные переменные
Затем мы можем скопировать значения из столбцов A и B в столбцы E и F, а затем использовать функцию IF() в Excel, чтобы определить две новые фиктивные переменные: Married и Divorced.
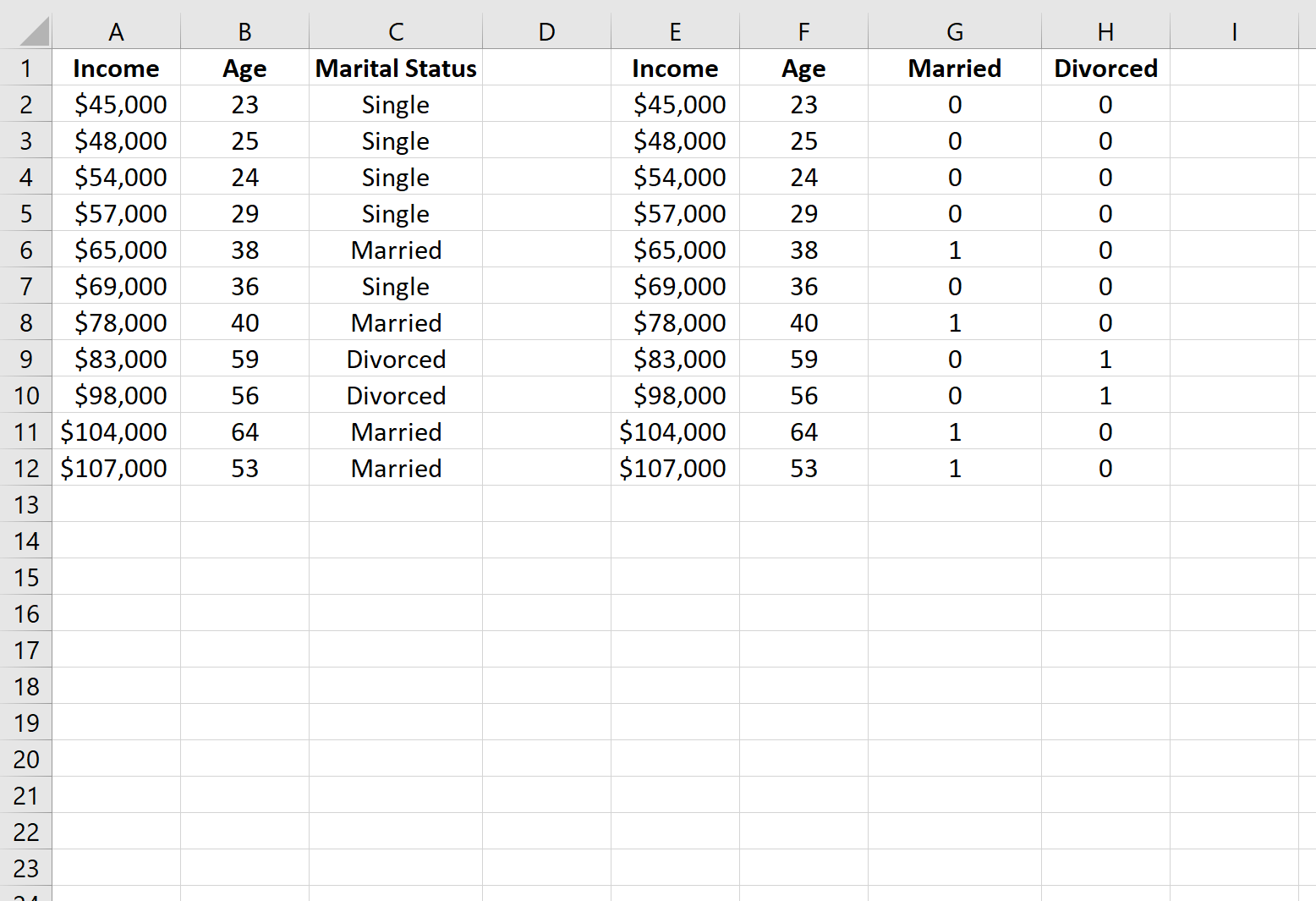
Вот формула, которую мы использовали в ячейке G2 , которую мы скопировали в остальные ячейки в столбце G:
= IF (C2 = "Married", 1, 0)
А вот формула, которую мы использовали в ячейке H2 , которую мы скопировали в остальные ячейки в столбце H:
= IF (C2 = "Divorced", 1, 0)
Затем мы можем использовать эти фиктивные переменные в регрессионной модели для прогнозирования дохода.
Шаг 3: выполните линейную регрессию
Чтобы выполнить множественную линейную регрессию, нам нужно щелкнуть вкладку « Данные » на верхней ленте, а затем « Анализ данных» в разделе « Анализ »:

Если вы не видите эту опцию доступной, вам нужно сначала загрузить пакет инструментов анализа .
В появившемся окне нажмите « Регрессия », а затем нажмите « ОК ».
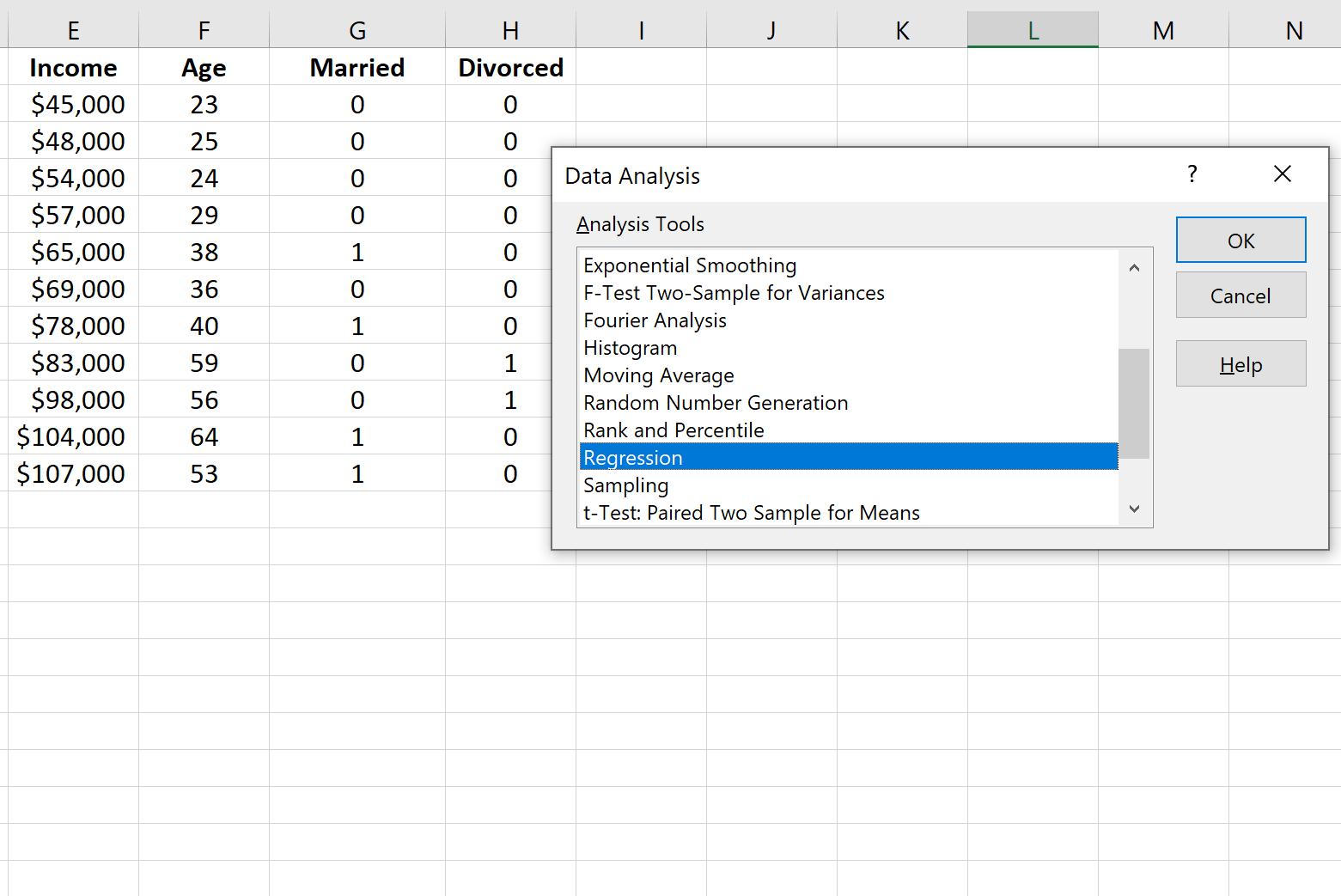
Затем заполните следующую информацию и нажмите OK .
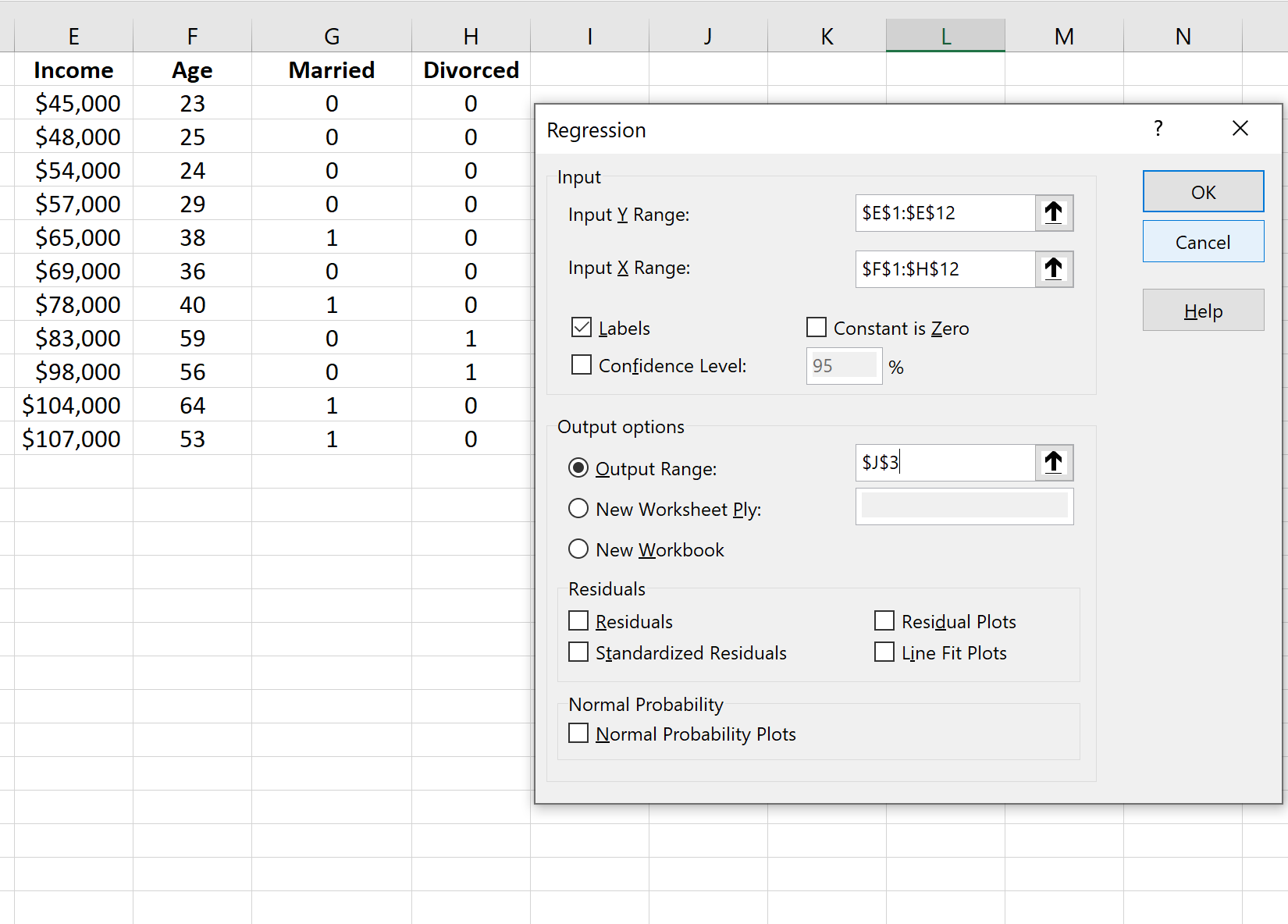
Это дает следующий результат:
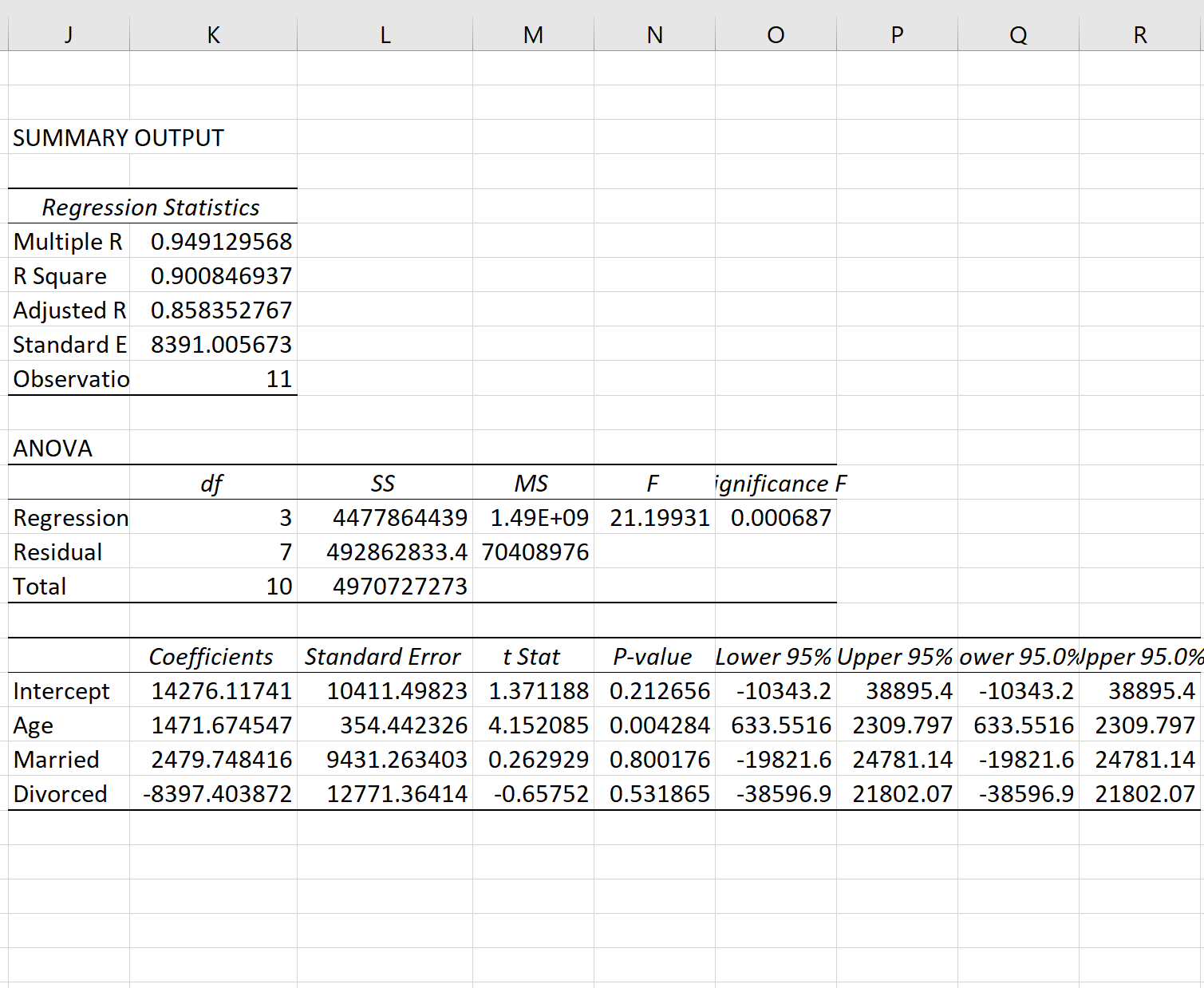
Из вывода мы видим, что подобранная линия регрессии:
Доход = 14 276,12 + 1 471,67*(возраст) + 2 479,75*(замужем) – 8 397,40*(разведен)
Мы можем использовать это уравнение, чтобы найти предполагаемый доход для человека в зависимости от его возраста и семейного положения. Например, доход 35-летнего человека, состоящего в браке, оценивается в 68 264 доллара США :
Доход = 14 276,12 + 1 471,67 * (35) + 2 479,75 * (1) - 8 397,40 * (0) = 68 264 доллара США.
Вот как интерпретировать коэффициенты регрессии из таблицы:
- Пересечение: Пересечение представляет собой средний доход одного человека в возрасте 0 лет. Поскольку человеку не может быть ноль лет, в этой конкретной регрессионной модели нет смысла интерпретировать саму точку пересечения.
- Возраст: каждый год увеличения возраста связан со средним увеличением дохода на 1471,67 доллара. Поскольку p-значение (0,004) меньше 0,05, возраст является статистически значимым предиктором дохода.
- Женат: женатый человек в среднем зарабатывает на 2479,75 долларов больше, чем одинокий человек. Поскольку p-значение (0,800) не менее 0,05, эта разница не является статистически значимой.
- Разведен: разведенный человек в среднем зарабатывает на 8 397,40 долларов меньше, чем одинокий человек. Поскольку p-значение (0,532) не менее 0,05, эта разница не является статистически значимой.
Поскольку обе фиктивные переменные не были статистически значимыми, мы могли исключить из модели семейное положение в качестве предиктора, поскольку оно, по-видимому, не добавляет никакой прогностической ценности для дохода.
Дополнительные ресурсы
Как выполнить простую линейную регрессию в Excel
Как рассчитать остаточную сумму квадратов в Excel
Как выполнить полиномиальную регрессию в Excel
Как создать остаточный график в Excel