U-критерий Манна-Уитни (иногда называемый критерием суммы рангов Уилкоксона) используется для сравнения различий между двумя выборками, когда распределение выборки не является нормальным, а размеры выборки малы (n < 30).
Он считается непараметрическим эквивалентом двухвыборочного t-критерия .
В этом руководстве объясняется, как выполнить U-критерий Манна-Уитни в Excel.
Пример: U-критерий Манна-Уитни в Excel
Исследователи хотят знать, приводит ли обработка топлива к изменению среднего расхода топлива на галлон автомобиля. Чтобы проверить это, они проводят эксперимент, в котором измеряют расход на галлон 12 автомобилей с обработкой топлива и 12 автомобилей без нее.
Поскольку размеры выборки малы и они подозревают, что распределение выборки не является нормальным, они решили выполнить U-критерий Манна-Уитни, чтобы определить, есть ли статистически значимая разница в милях на галлон между двумя группами.
Выполните следующие шаги, чтобы провести U-критерий Манна-Уитни в Excel.
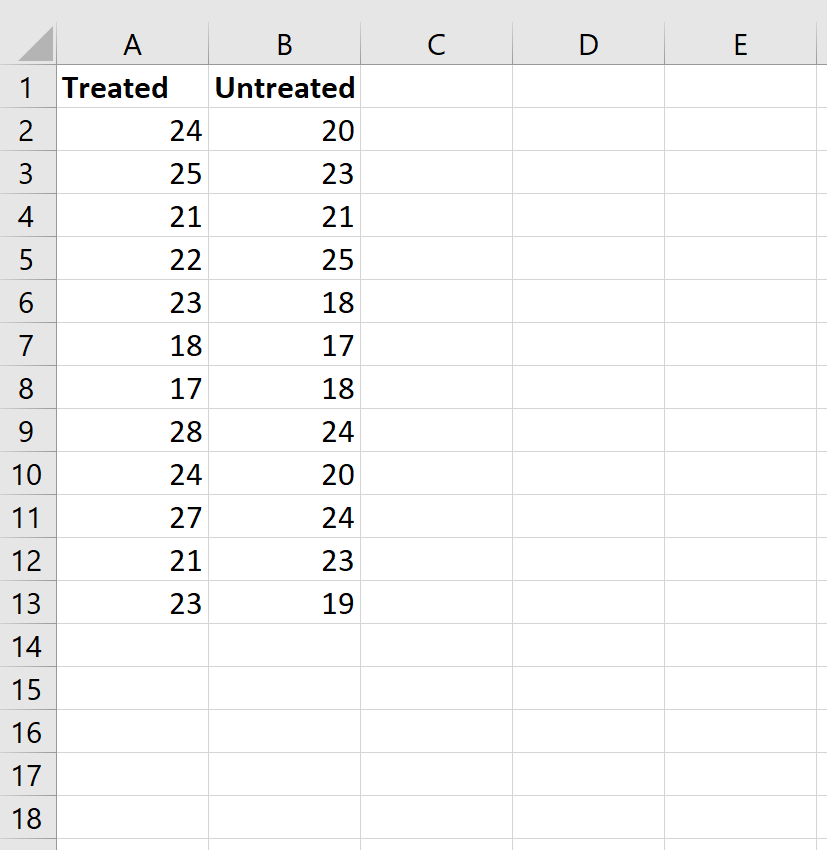
Шаг 1: Введите данные.
Введите данные следующим образом:
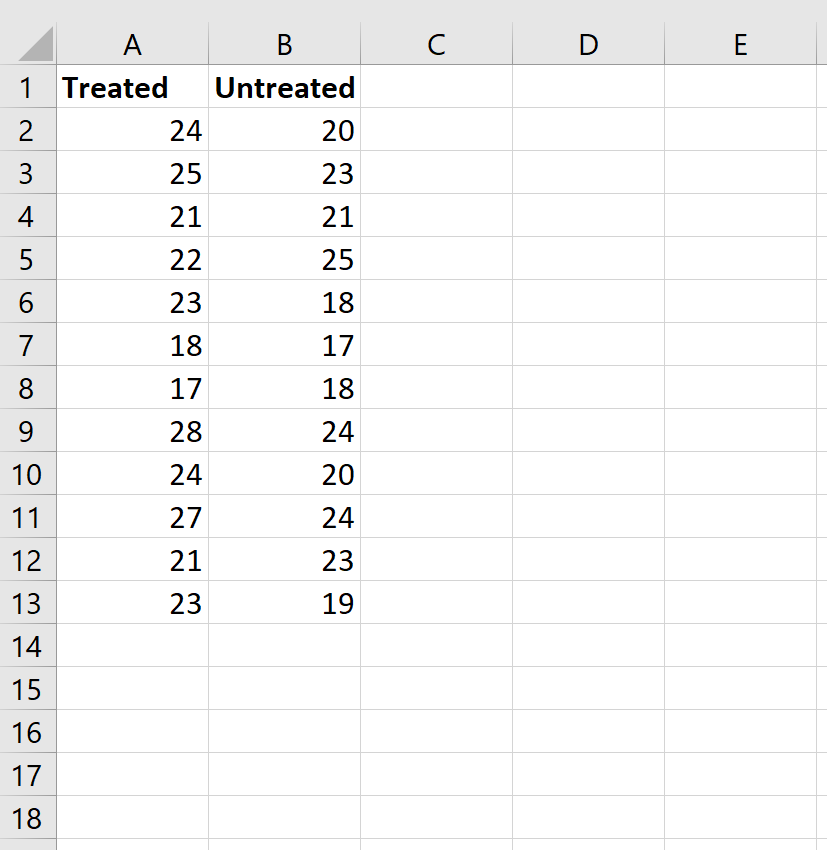
Шаг 2: Рассчитайте ранги для обеих групп.
Далее мы рассчитаем ранги для каждой группы. На следующем изображении показана формула, используемая для расчета ранга первого значения в группе обработанных:
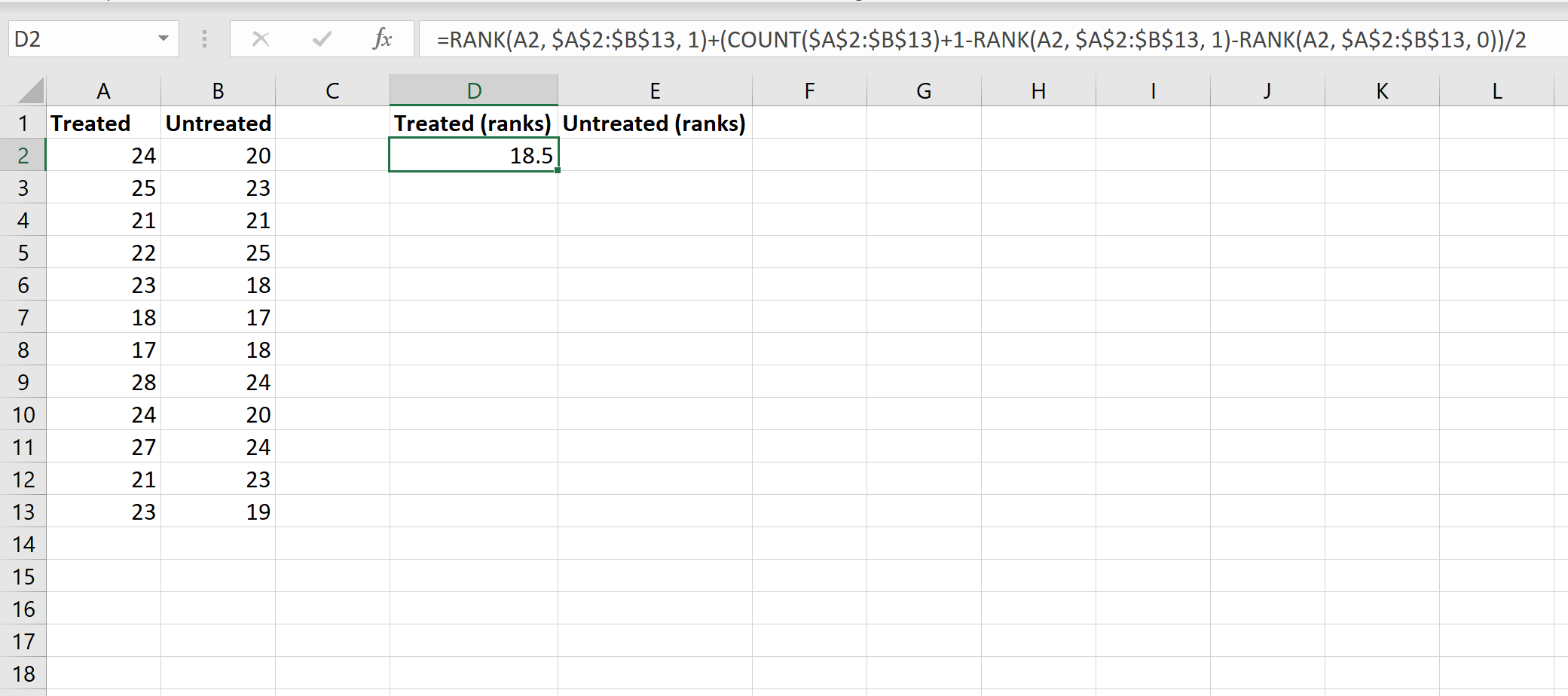
Хотя эта формула довольно сложна, вам нужно ввести ее только один раз. Затем вы можете просто перетащить формулу во все остальные ячейки, чтобы заполнить ранги:
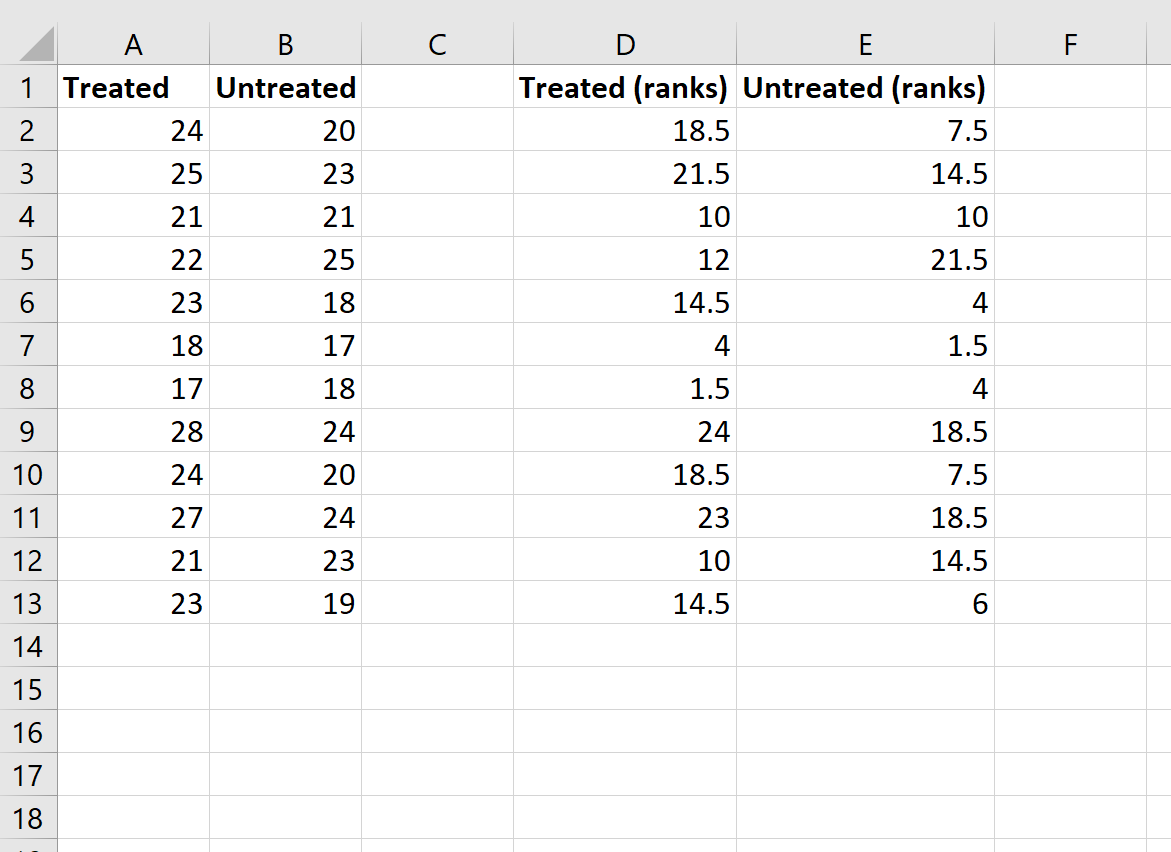
Шаг 3: Рассчитайте необходимые значения для тестовой статистики.
Затем мы будем использовать следующие формулы для расчета суммы рангов для каждой группы, размера выборки для каждой группы, статистики U-теста для каждой группы и общей статистики U-теста:
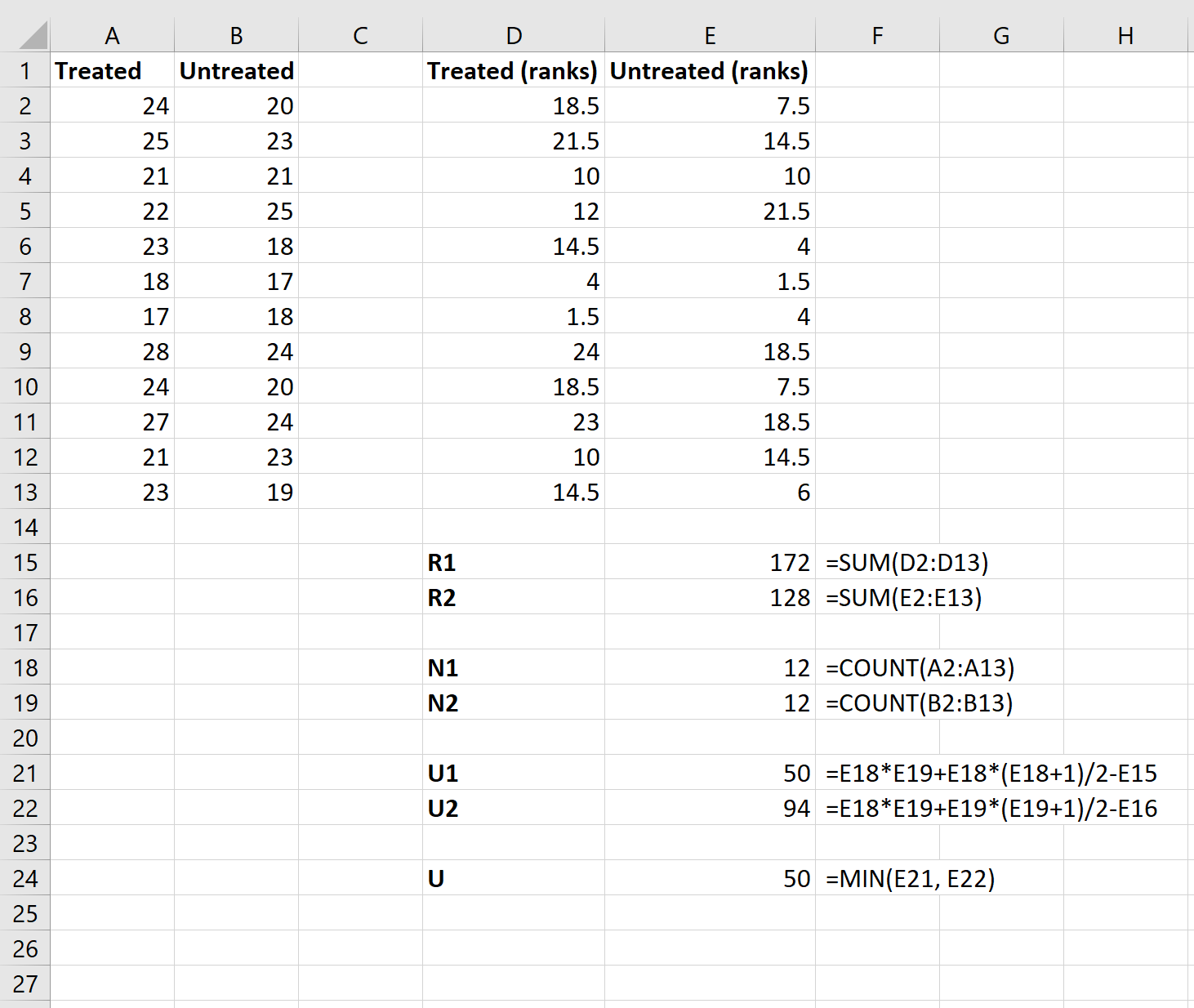
Шаг 4: Рассчитайте статистику теста z и соответствующее значение p.
Наконец, мы будем использовать следующие формулы для расчета статистики теста z и соответствующего значения p, чтобы определить, должны ли мы отклонить или не отклонить нулевую гипотезу:
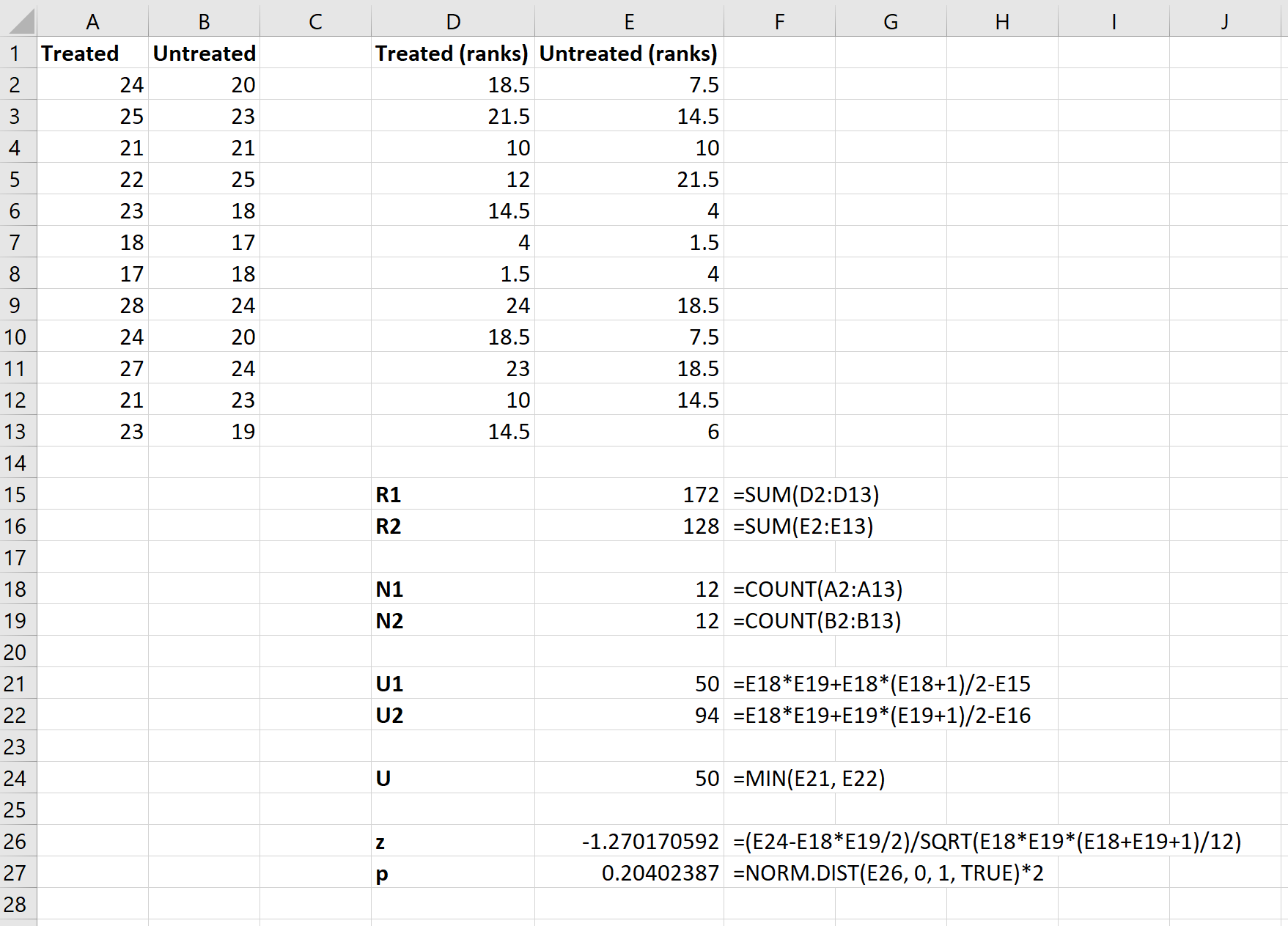
Нулевая гипотеза теста утверждает, что две группы имеют одинаковое среднее значение расхода топлива на галлон. Поскольку p-значение теста ( 0,20402387 ) не меньше нашего уровня значимости 0,05, мы не можем отвергнуть нулевую гипотезу.
У нас нет достаточных доказательств, чтобы сказать, что истинное среднее значение расхода на галлон отличается между двумя группами.