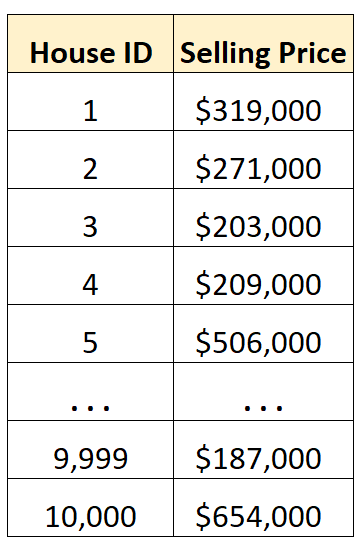
Медиана представляет собой среднее значение набора данных, когда все значения расположены от наименьшего к наибольшему.
Например, медиана в следующем наборе данных равна 19:
Набор данных: 3, 4, 11, 15, 19 , 22, 23, 23, 26
Медиана также представляет собой 50 -й процентиль набора данных. То есть ровно половина значений в наборе данных больше медианы, а половина значений меньше.
Медиана — важная метрика для расчета, потому что она дает нам представление о том, где находится «центр» набора данных. Это также дает нам представление о «типичном» значении в данном наборе данных.
Например, предположим, что у нас есть набор данных, содержащий цену продажи 10 000 различных домов в определенном городе.
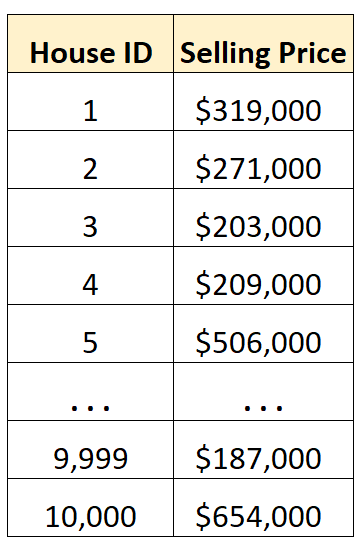
Вместо того, чтобы рассматривать ряды необработанных данных , мы можем рассчитать медианное значение, чтобы быстро понять среднюю цену продажи домов в этом городе.
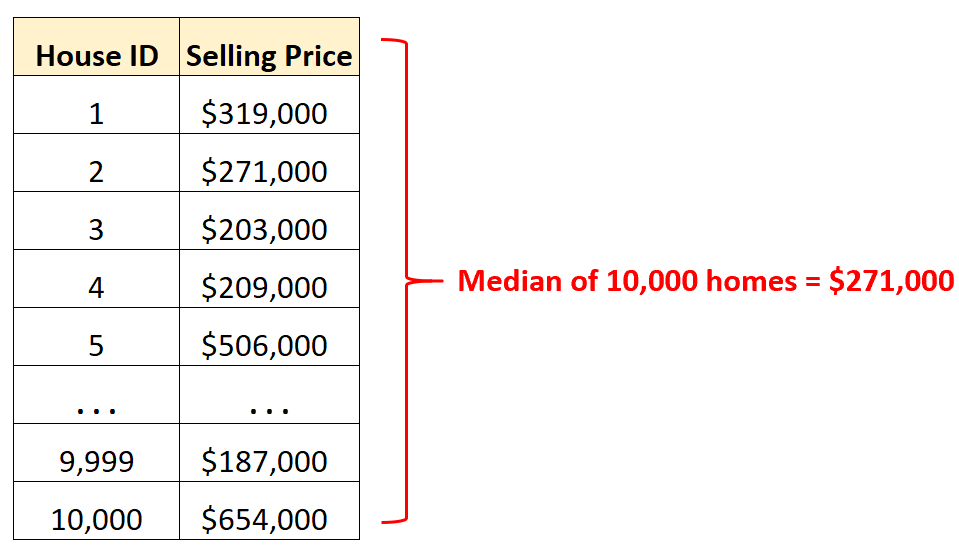
Зная, что медианная цена продажи составляет 271 000 долларов, мы знаем, что ровно половина из 10 000 домов продана дороже этой суммы, а половина — дешевле.
Это также дает нам представление о «типичной» цене продажи домов в этом городе.
Когда использовать медиану
При анализе наборов данных нам часто интересно понять, где находится центральное значение.
В статистике есть две общие метрики, которые мы используем для измерения центра набора данных:
- Среднее : среднее значение в наборе данных.
- Медиана : среднее значение в наборе данных.
Оказывается, медиана является более полезной метрикой в следующих обстоятельствах:
- Когда распределение искажено .
- Когда дистрибутив содержит выбросы.
Чтобы проиллюстрировать это, рассмотрим следующие два примера.
Пример 1: вычисление медианы асимметричного распределения
Рассмотрим следующее распределение заработной платы жителей определенного города:
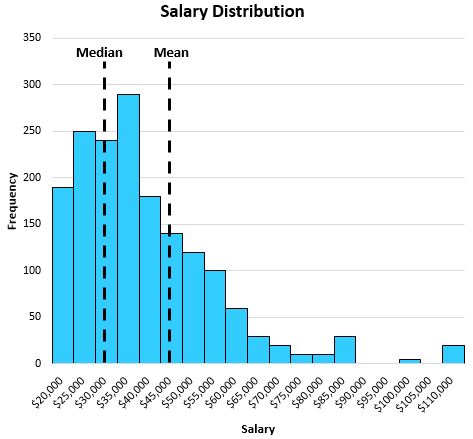
Медиана лучше отражает «типичную» заработную плату резидента, чем среднее, потому что распределение смещено вправо.
Это означает, что большие зарплаты в правой части распределения отодвигают среднее значение от центра распределения.
В этом конкретном примере средняя зарплата составляет 47 000 долларов, а медианная зарплата — 32 000 долларов. Медиана гораздо более репрезентативна для типичной зарплаты в этом городе.
Пример 2: Расчет медианы при наличии выбросов
Рассмотрим следующую диаграмму, которая показывает площадь домов на определенной улице:
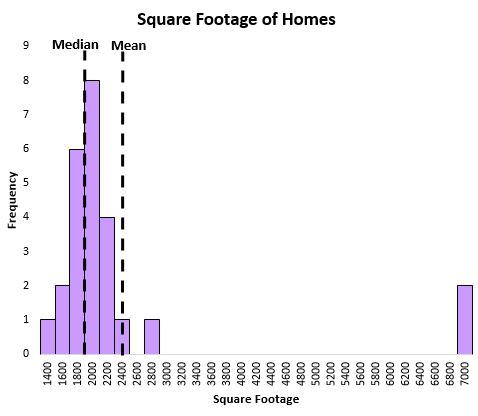
На среднее значение сильно влияет пара очень больших домов, а на медиану - нет.
Мы можем видеть, что медиана лучше отражает «типичную» площадь дома на этой улице по сравнению со средним значением, потому что на нее не влияют экстремальные значения выбросов.
Резюме
Вот краткое изложение основных моментов, сделанных в этой статье:
- Медиана представляет среднее значение в наборе данных.
- Медиана важна, потому что она дает нам представление о том, где находится центральное значение в наборе данных.
- Медиана имеет тенденцию быть более полезной для расчета, чем среднее значение, когда распределение асимметрично и/или имеет выбросы.
Дополнительные ресурсы
Примеры из реальной жизни: использование среднего, медианы и моды
Когда использовать среднее значение против медианы (с примерами)
Почему режим важен в статистике?