В статистике диапазон представляет собой разницу между наименьшим и наибольшим значением в наборе данных.
Например, предположим, что у нас есть следующий набор данных:
Набор данных: 3, 4, 11, 15, 19, 19, 19, 22, 22, 23, 23, 26
Мы можем использовать следующую формулу для расчета диапазона:
- Диапазон = Максимальное значение – Минимальное значение
- Диапазон = 26 – 3
- Диапазон = 23
Диапазон составляет 23.Представляет собой разницу между наименьшим и наибольшим значениями в наборе данных.
В статистике диапазон важен по следующим причинам:
Причина 1 : это говорит нам о распространении всего набора данных.
Причина 2 : сообщает нам, какие экстремальные значения возможны в данном наборе данных.
Следующие примеры иллюстрируют каждую из этих причин на практике.
Причина 1: диапазон говорит нам о разбросе всего набора данных
Диапазон говорит нам о распространении всего набора данных.
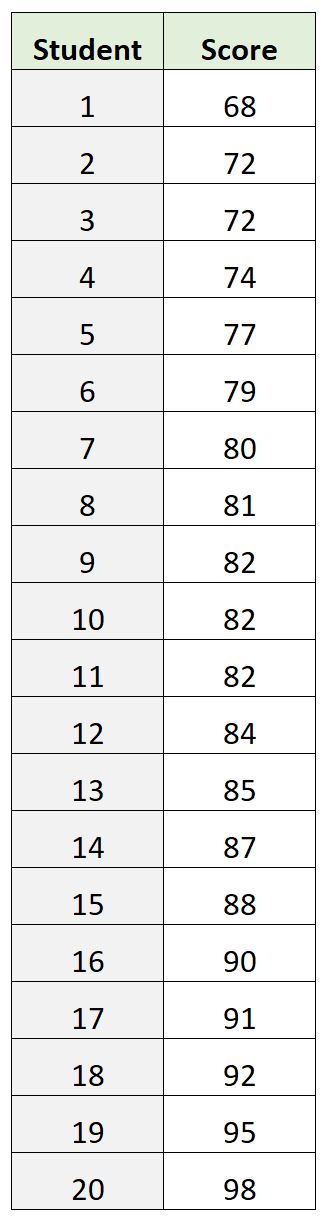
Например, предположим, что у нас есть следующий набор данных, который показывает результаты экзаменов 20 разных учеников в классе:
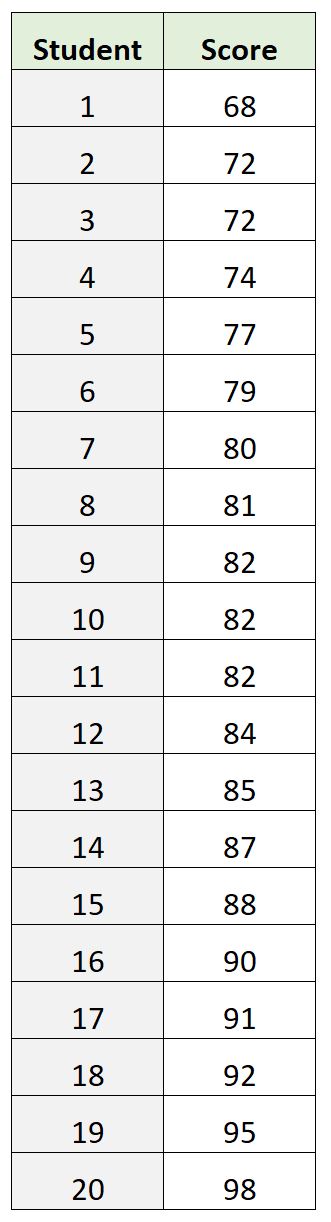
Диапазон экзаменационных баллов будет рассчитываться как:
- Диапазон = Максимальное значение – Минимальное значение
- Диапазон = 98 – 68
- Диапазон = 30
Диапазон оказывается равным 30.Это представляет собой разницу между самой высокой оценкой экзамена и самой низкой оценкой экзамена в классе.
Зная только эту метрику, учитель класса может быстро получить представление о разбросе значений экзаменационных баллов среди всех учащихся.
Причина 2: Диапазон говорит нам, какие экстремальные значения возможны в данном наборе данных.
Диапазон говорит нам, какие экстремальные значения возможны в данном наборе данных.
Например, предположим, что у риелтора есть доступ к базе данных, содержащей цену продажи 100 000 домов в определенном городе в США:
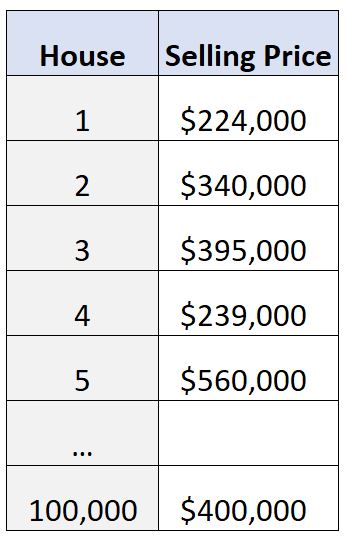
Предположим, мы используем какое-то статистическое программное обеспечение (например, Excel , R , Python и т. д.), чтобы вычислить диапазон этого набора данных и найти следующее:
- Диапазон = Максимальное значение – Минимальное значение
- Диапазон = 854 000 – 194 000
- Диапазон = 660 000
Если у риелтора есть клиент с бюджетом на покупку менее 194 000 долларов или более 854 000 долларов, риелтор может сразу узнать, что в этом конкретном городе не будет домов, соответствующих критериям покупки.
Недостаток использования диапазона
Диапазон имеет один недостаток: на него влияют выбросы .
Чтобы проиллюстрировать это, рассмотрим следующий набор данных:
Набор данных: 1, 4, 8, 11, 13, 17, 19, 19, 20, 23, 24, 24, 25, 28, 29, 31, 32
Диапазон этого набора данных составляет 32 – 1 = 31 .
Однако подумайте, есть ли в наборе данных один экстремальный выброс:
Набор данных: 1, 4, 8, 11, 13, 17, 19, 19, 20, 23, 24, 24, 25, 28, 29, 31, 32, 378
Диапазон этого набора данных теперь будет 378 – 1 = 377 .
Обратите внимание, как резко меняется диапазон в результате одного выброса.
Перед вычислением диапазона любого набора данных рекомендуется сначала проверить, нет ли каких-либо выбросов, которые могут привести к тому, что диапазон будет вводить в заблуждение.
Дополнительные ресурсы
В следующих руководствах объясняется важность других показателей в статистике:
Почему среднее значение важно в статистике?
Почему медиана важна в статистике?
Почему режим важен в статистике?
Почему стандартное отклонение важно в статистике?