Лассо-регрессия — это метод, который мы можем использовать для подбора модели регрессии, когда в данных присутствует мультиколлинеарность .
В двух словах, регрессия методом наименьших квадратов пытается найти оценки коэффициентов, которые минимизируют сумму квадратов остатков (RSS):
RSS = Σ(y i – ŷ i )2
куда:
- Σ : греческий символ, означающий сумму
- y i : Фактическое значение отклика для i -го наблюдения
- ŷ i : прогнозируемое значение отклика на основе модели множественной линейной регрессии.
И наоборот, регрессия лассо стремится минимизировать следующее:
RSS + λΣ|β j |
где j находится в диапазоне от 1 до p переменных-предикторов и λ ≥ 0.
Этот второй член уравнения известен как штраф за усадку.В регрессии лассо мы выбираем значение для λ, которое дает наименьшую возможную тестовую MSE (среднеквадратическую ошибку).
В этом руководстве представлен пошаговый пример выполнения регрессии лассо в R.
Шаг 1: Загрузите данные
В этом примере мы будем использовать встроенный набор данных R под названием mtcars.Мы будем использовать hp в качестве переменной ответа и следующие переменные в качестве предикторов:
- миль на галлон
- вес
- дрянь
- qсек
Для выполнения лассо-регрессии мы будем использовать функции из пакета glmnet.Этот пакет требует, чтобы переменная ответа была вектором, а набор переменных-предикторов имел класс data.matrix .
Следующий код показывает, как определить наши данные:
#define response variable
y <- mtcars$hp
#define matrix of predictor variables
x <- data.matrix(mtcars[, c('mpg', 'wt', 'drat', 'qsec')])
Шаг 2: Подберите модель регрессии Лассо
Далее мы воспользуемся функцией glmnet() , чтобы подобрать модель регрессии лассо, и укажем alpha=1 .
Обратите внимание, что установка альфы равной 0 эквивалентна использованию гребневой регрессии , а установка альфы на некоторое значение от 0 до 1 эквивалентна использованию эластичной сети.
Чтобы определить, какое значение использовать для лямбда, мы выполним k-кратную перекрестную проверку и определим значение лямбда, которое дает наименьшую среднеквадратичную ошибку теста (MSE).
Обратите внимание, что функция cv.glmnet() автоматически выполняет k-кратную перекрестную проверку, используя k = 10 кратностей.
library (glmnet)
#perform k-fold cross-validation to find optimal lambda value
cv_model <- cv. glmnet (x, y, alpha = 1 )
#find optimal lambda value that minimizes test MSE
best_lambda <- cv_model$ lambda.min
best_lambda
[1] 5.616345
#produce plot of test MSE by lambda value
plot(cv_model)
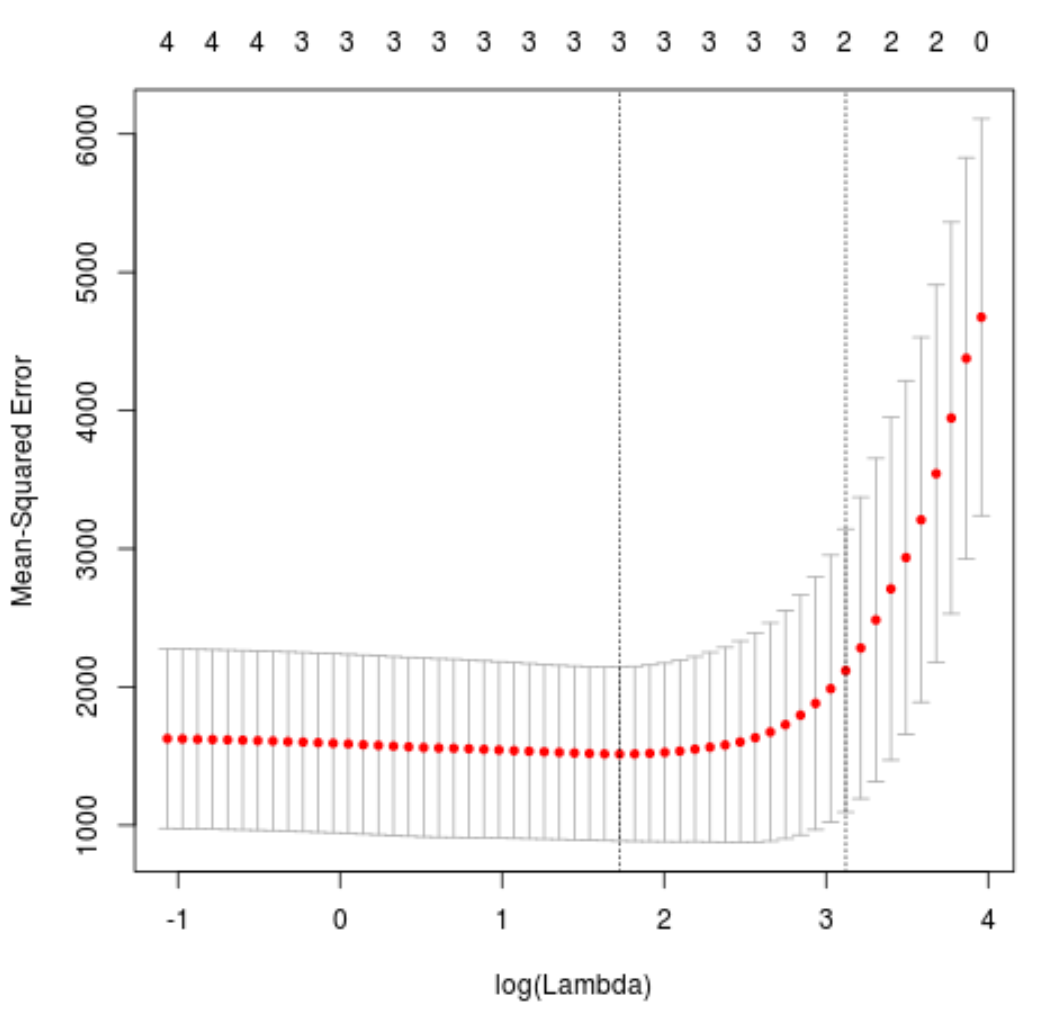
Значение лямбда, минимизирующее тестовую MSE, оказывается равным 5,616345 .
Шаг 3: Анализ окончательной модели
Наконец, мы можем проанализировать окончательную модель, полученную с помощью оптимального значения лямбда.
Мы можем использовать следующий код, чтобы получить оценки коэффициентов для этой модели:
#find coefficients of best model
best_model <- glmnet(x, y, alpha = 1 , lambda = best_lambda)
coef(best_model)
5 x 1 sparse Matrix of class "dgCMatrix"
s0
(Intercept) 484.20742
mpg -2.95796
wt 21.37988
drat.
qsec -19.43425
Коэффициент для предиктора drat не показан, потому что регрессия лассо уменьшила коэффициент до нуля. Это означает, что он был полностью исключен из модели, потому что не имел достаточного влияния.
Обратите внимание, что это ключевое различие между регрессией гребня и регрессией лассо.Гребневая регрессия сужает все коэффициенты до нуля, но лассо-регрессия может удалить предикторы из модели, полностью сведя коэффициенты к нулю.
Мы также можем использовать окончательную модель регрессии лассо, чтобы делать прогнозы на основе новых наблюдений. Например, предположим, что у нас есть новый автомобиль со следующими атрибутами:
- миль на галлон: 24
- вес: 2,5
- Драт: 3,5
- qсек: 18,5
В следующем коде показано, как использовать подобранную модель регрессии лассо для прогнозирования значения hp этого нового наблюдения:
#define new observation
new = matrix(c(24, 2.5, 3.5, 18.5), nrow= 1 , ncol= 4 )
#use lasso regression model to predict response value
predict(best_model, s = best_lambda, newx = new)
[1,] 109.0842
Основываясь на входных значениях, модель предсказывает, что этот автомобиль будет иметь значение 109,0842 л.с.
Наконец, мы можем рассчитатьR-квадрат модели на данных обучения:
#use fitted best model to make predictions
y_predicted <- predict (best_model, s = best_lambda, newx = x)
#find SST and SSE
sst <- sum ((y - mean (y))^2)
sse <- sum ((y_predicted - y)^2)
#find R-Squared
rsq <- 1 - sse/sst
rsq
[1] 0.8047064
R-квадрат оказывается равным 0,8047064.То есть лучшая модель смогла объяснить 80,47% вариации значений отклика обучающих данных.
Полный код R, использованный в этом примере, вы можете найти здесь .