В обычной множественной линейной регрессии мы используем набор переменных-предикторов p и переменную ответа , чтобы соответствовать модели формы:
Y = β 0 + β 1 X 1 + β 2 X 2 + … + β p X p + ε
куда:
- Y : переменная ответа
- X j : j -я предикторная переменная
- β j : среднее влияние на Y увеличения X j на одну единицу при неизменности всех остальных предикторов.
- ε : Член ошибки
Значения β 0 , β 1 , B 2 , … , β p выбираются методом наименьших квадратов , который минимизирует сумму квадратов невязок (RSS):
RSS = Σ(y i – ŷ i ) 2
куда:
- Σ : греческий символ, означающий сумму
- y i : Фактическое значение отклика для i -го наблюдения
- ŷ i : прогнозируемое значение отклика на основе модели множественной линейной регрессии.
Однако, когда переменные-предикторы сильно коррелированы, мультиколлинеарность может стать проблемой. Это может привести к тому, что оценки коэффициентов модели будут ненадежными и будут иметь высокую дисперсию.
Один из способов обойти эту проблему без полного удаления некоторых переменных-предикторов из модели — использовать метод, известный как гребневая регрессия , который вместо этого стремится свести к минимуму следующее:
RSS + λΣβ j 2
где j находится в диапазоне от 1 до p и λ ≥ 0.
Этот второй член уравнения известен как штраф за усадку .
Когда λ = 0, этот штрафной член не действует, и гребневая регрессия дает те же оценки коэффициентов, что и метод наименьших квадратов. Однако по мере того, как λ приближается к бесконечности, штраф за усадку становится более влиятельным, и оценки коэффициента гребневой регрессии приближаются к нулю.
Как правило, переменные-предикторы, которые меньше всего влияют на модель, будут уменьшаться до нуля быстрее всего.
Зачем использовать гребневую регрессию?
Преимущество гребенчатой регрессии по сравнению с регрессией наименьших квадратов заключается в компромиссе смещения и дисперсии .
Напомним, что среднеквадратическая ошибка (MSE) — это показатель, который мы можем использовать для измерения точности данной модели, и он рассчитывается как:
MSE = Var( f̂( x0)) + [Bias( f̂( x0))] 2 + Var(ε)
MSE = дисперсия + погрешность 2 + неустранимая ошибка
Основная идея гребневой регрессии состоит в том, чтобы ввести небольшое смещение, чтобы можно было существенно уменьшить дисперсию, что приводит к более низкому общему значению MSE.
Чтобы проиллюстрировать это, рассмотрим следующую диаграмму:
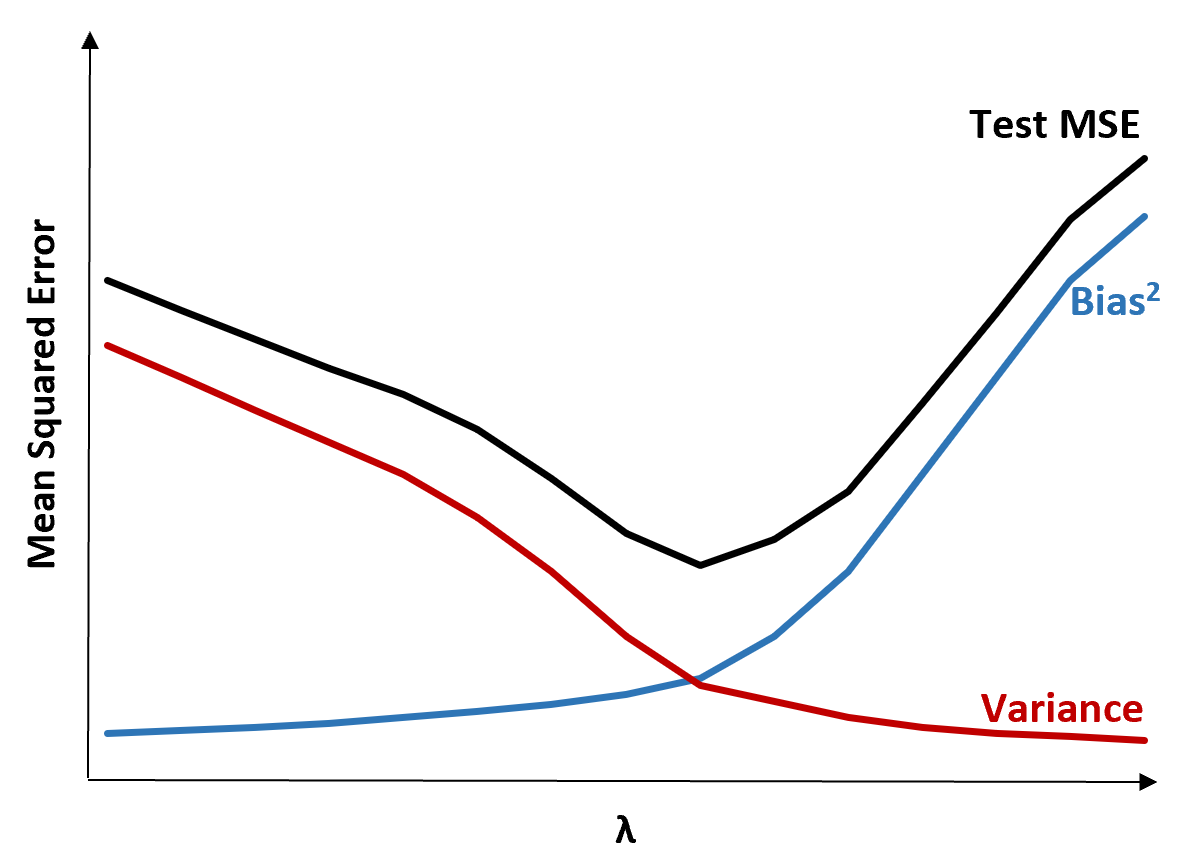
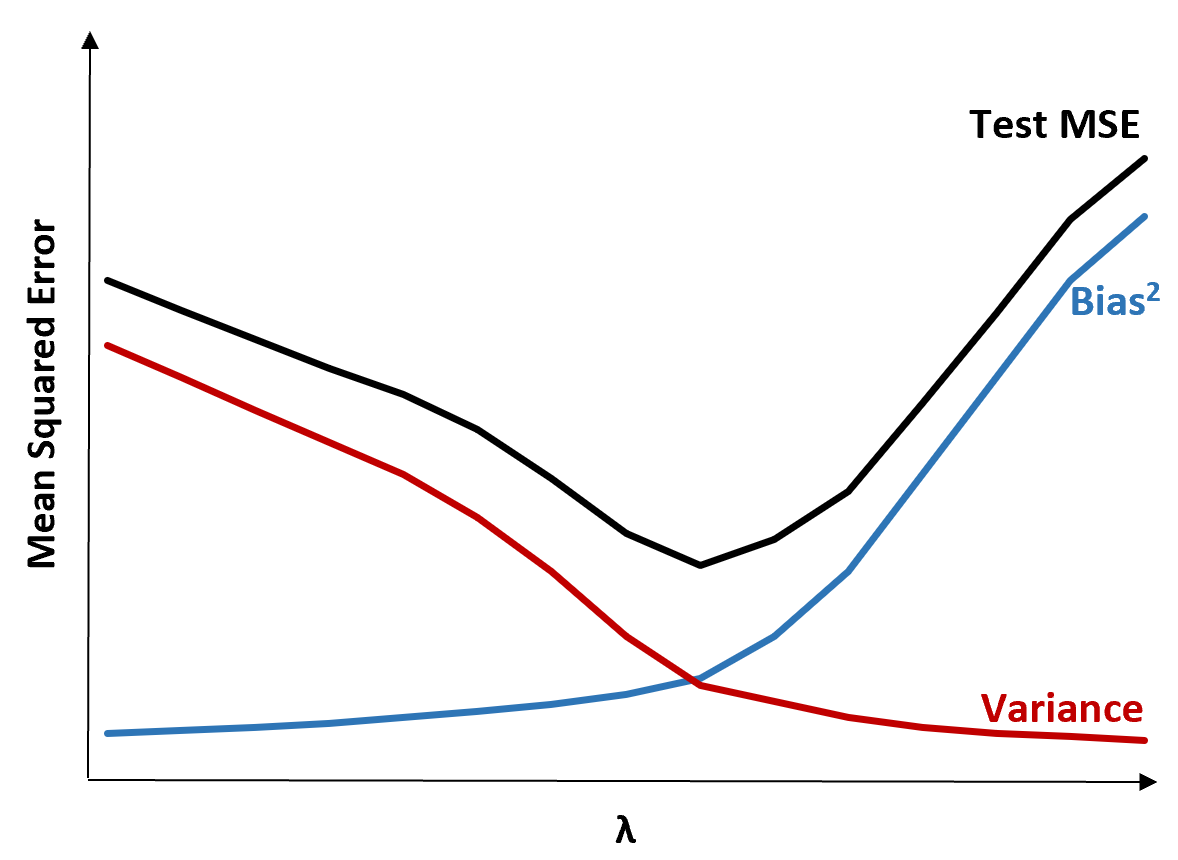
Обратите внимание, что по мере увеличения λ дисперсия существенно падает с очень небольшим увеличением смещения. Однако после определенного момента дисперсия уменьшается менее быстро, а сокращение коэффициентов приводит к их значительному недооцениванию, что приводит к значительному увеличению систематической ошибки.
Из диаграммы видно, что тестовая MSE является самой низкой, когда мы выбираем значение для λ, которое обеспечивает оптимальный компромисс между смещением и дисперсией.
Когда λ = 0, штрафной член в гребневой регрессии не имеет эффекта и, таким образом, дает те же оценки коэффициентов, что и метод наименьших квадратов. Однако, увеличивая λ до определенной точки, мы можем уменьшить общую тестовую MSE.
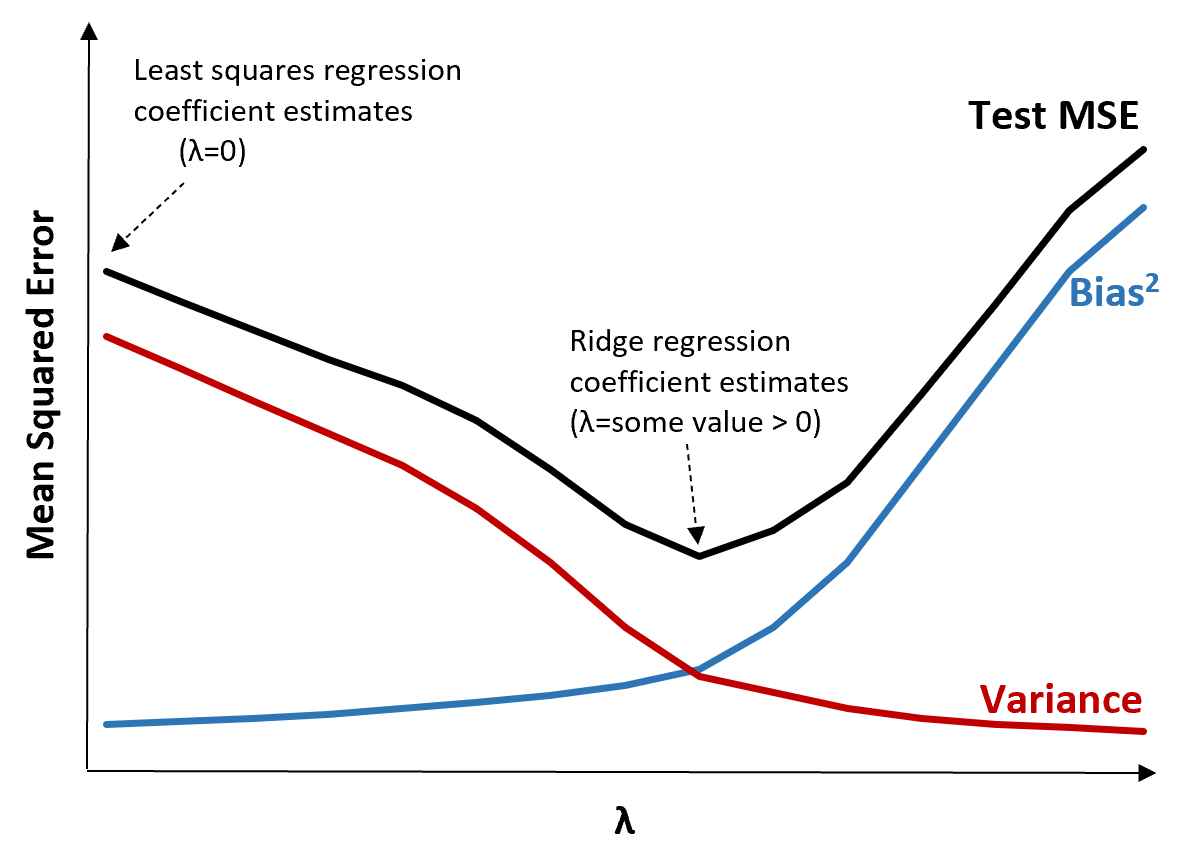
Это означает, что модель, подобранная с помощью гребневой регрессии, будет давать меньшие ошибки теста, чем модель, подобранная с помощью регрессии наименьших квадратов.
Шаги для выполнения гребневой регрессии на практике
Для выполнения гребневой регрессии можно использовать следующие шаги:
Шаг 1: Рассчитайте матрицу корреляции и значения VIF для переменных-предикторов.
Во-первых, мы должны создать корреляционную матрицу и вычислить значения VIF (фактор инфляции дисперсии) для каждой переменной-предиктора.
Если мы обнаружим высокую корреляцию между переменными-предикторами и высокими значениями VIF (в некоторых текстах «высокое» значение VIF определяется как 5, а в других используется 10), то, вероятно, целесообразно использовать гребневую регрессию.
Однако, если в данных нет мультиколлинеарности, то, возможно, в первую очередь нет необходимости выполнять гребневую регрессию. Вместо этого мы можем выполнить обычную регрессию методом наименьших квадратов.
Шаг 2: Стандартизируйте каждую предикторную переменную.
Перед выполнением гребневой регрессии мы должны масштабировать данные таким образом, чтобы каждая переменная-предиктор имела среднее значение 0 и стандартное отклонение 1. Это гарантирует, что ни одна переменная-предиктор не будет чрезмерно влиять при выполнении гребневой регрессии.
Шаг 3: Подберите модель гребневой регрессии и выберите значение для λ.
Не существует точной формулы, которую мы могли бы использовать, чтобы определить, какое значение использовать для λ. На практике есть два распространенных способа выбора λ:
(1) Создайте график трассировки Риджа. Это график, который визуализирует значения оценок коэффициентов по мере того, как λ увеличивается до бесконечности. Обычно мы выбираем λ как значение, при котором большинство оценок коэффициентов начинают стабилизироваться.
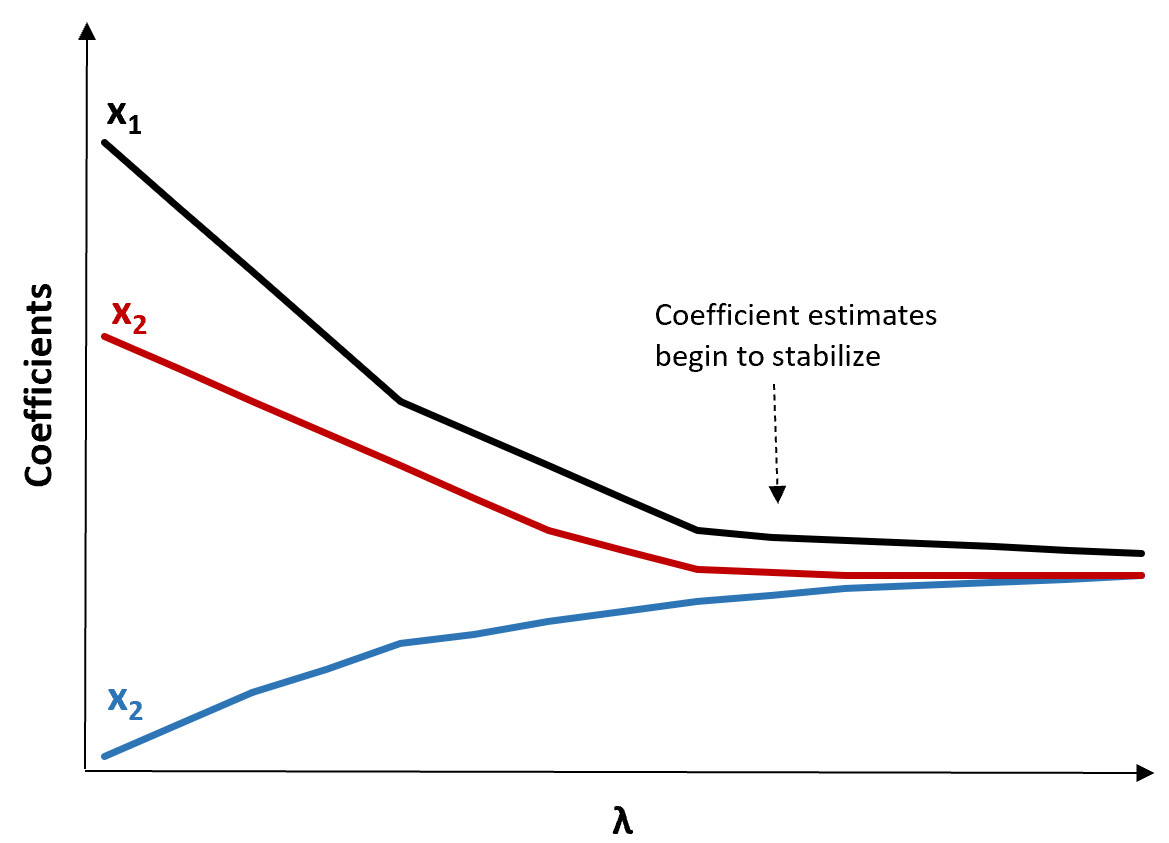
(2) Рассчитайте тест MSE для каждого значения λ.
Другой способ выбрать λ состоит в том, чтобы просто вычислить тестовую MSE каждой модели с разными значениями λ и выбрать λ как значение, которое дает наименьшую тестовую MSE.
Плюсы и минусы хребтовой регрессии
Самым большим преимуществом гребневой регрессии является ее способность давать более низкую среднеквадратичную ошибку теста (MSE) по сравнению с регрессией наименьших квадратов, когда присутствует мультиколлинеарность.
Однако самым большим недостатком гребневой регрессии является ее неспособность выполнять выбор переменных, поскольку она включает все переменные-предикторы в окончательную модель. Поскольку некоторые предикторы будут сжаты очень близко к нулю, это может затруднить интерпретацию результатов модели.
На практике гребенчатая регрессия может создать модель, которая может давать более точные прогнозы по сравнению с моделью наименьших квадратов, но часто бывает сложнее интерпретировать результаты модели.
В зависимости от того, что для вас более важно: интерпретация модели или точность прогноза, вы можете использовать обычный метод наименьших квадратов или гребенчатую регрессию в различных сценариях.
Ридж-регрессия в R & Python
В следующих руководствах объясняется, как выполнить регрессию гребня в R и Python, двух наиболее распространенных языках, используемых для подбора моделей регрессии гребня:
Регрессия хребта в R (шаг за шагом)
Ридж-регрессия в Python (шаг за шагом)