Линейный дискриминантный анализ — это метод, который вы можете использовать, когда у вас есть набор переменных-предикторов, и вы хотите классифицировать переменную ответа по двум или более классам.
В этом руководстве представлен пошаговый пример выполнения линейного дискриминантного анализа в R.
Шаг 1: Загрузите необходимые библиотеки
Во-первых, мы загрузим необходимые библиотеки для этого примера:
library (MASS)
library (ggplot2)
Шаг 2: Загрузите данные
В этом примере мы будем использовать встроенный набор данных iris в R. Следующий код показывает, как загрузить и просмотреть этот набор данных:
#attach *iris* dataset to make it easy to work with
attach(iris)
#view structure of dataset
str(iris)
'data.frame': 150 obs. of 5 variables:
$ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
$ Sepal.Width : num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
$ Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
$ Petal.Width : num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
$ Species : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 ...
Мы видим, что набор данных содержит 5 переменных и 150 общих наблюдений.
В этом примере мы построим модель линейного дискриминантного анализа, чтобы классифицировать, к какому виду принадлежит данный цветок.
Мы будем использовать следующие переменные-предикторы в модели:
- Длина чашелистика
- Сепал.Ширина
- Лепесток.Длина
- Лепесток.Ширина
И мы будем использовать их для прогнозирования переменной отклика Species , которая принимает следующие три потенциальных класса:
- сетоза
- лишай
- виргиния
Шаг 3: Масштабируйте данные
Одно из ключевых предположений линейного дискриминантного анализа состоит в том, что все переменные-предикторы имеют одинаковую дисперсию. Простой способ убедиться, что это предположение выполняется, — масштабировать каждую переменную таким образом, чтобы ее среднее значение равнялось 0, а стандартное отклонение — 1.
Мы можем быстро сделать это в R, используя функцию scale() :
#scale each predictor variable (i.e. first 4 columns)
iris[1:4] <- scale(iris[1:4])
Мы можем использовать функцию apply(), чтобы убедиться, что каждая предикторная переменная теперь имеет среднее значение 0 и стандартное отклонение 1:
#find mean of each predictor variable
apply(iris[1:4], 2, mean)
Sepal.Length Sepal.Width Petal.Length Petal.Width
-4.484318e-16 2.034094e-16 -2.895326e-17 -3.663049e-17
#find standard deviation of each predictor variable
apply(iris[1:4], 2, sd)
Sepal.Length Sepal.Width Petal.Length Petal.Width
1 1 1 1
Шаг 4. Создайте обучающую и тестовую выборки
Затем мы разделим набор данных на обучающий набор для обучения модели и тестовый набор для проверки модели:
#make this example reproducible
set.seed(1)
#Use 70% of dataset as training set and remaining 30% as testing set
sample <- sample(c( TRUE , FALSE ), nrow (iris), replace = TRUE , prob =c(0.7,0.3))
train <- iris[sample, ]
test <- iris[!sample, ]
Шаг 5: Соответствуйте модели LDA
Далее мы воспользуемся функцией lda() из пакета MASS , чтобы подогнать модель LDA к нашим данным:
#fit LDA model
model <- lda(Species~., data=train)
#view model output
model
Call:
lda(Species ~ ., data = train)
Prior probabilities of groups:
setosa versicolor virginica
0.3207547 0.3207547 0.3584906
Group means:
Sepal.Length Sepal.Width Petal.Length Petal.Width
setosa -1.0397484 0.8131654 -1.2891006 -1.2570316
versicolor 0.1820921 -0.6038909 0.3403524 0.2208153
virginica 0.9582674 -0.1919146 1.0389776 1.1229172
Coefficients of linear discriminants:
LD1 LD2
Sepal.Length 0.7922820 0.5294210
Sepal.Width 0.5710586 0.7130743
Petal.Length -4.0762061 -2.7305131
Petal.Width -2.0602181 2.6326229
Proportion of trace:
LD1 LD2
0.9921 0.0079
Вот как интерпретировать вывод модели:
Априорные вероятности группы: они представляют пропорции каждого вида в обучающей выборке. Например, 35,8% всех наблюдений в обучающей выборке относились к видам virginica .
Групповые средние: они отображают средние значения для каждой предикторной переменной для каждого вида.
Коэффициенты линейных дискриминантов: они отображают линейную комбинацию переменных-предикторов, которые используются для формирования решающего правила модели LDA. Например:
- LD1: .792*Длина чашелистика + .571*Ширина чашелистика – 4,076*Длина лепестка – 2,06*Ширина лепестка
- LD2: .529*Длина чашелистика + .713*Ширина чашелистика – 2,731*Длина лепестка + 2,63*Ширина лепестка
Доля трассы: они отображают процентное разделение, достигнутое каждой линейной дискриминантной функцией.
Шаг 6: Используйте модель для прогнозирования
После того, как мы подогнали модель, используя наши обучающие данные, мы можем использовать ее для прогнозирования наших тестовых данных:
#use LDA model to make predictions on test data
predicted <- predict (model, test)
names(predicted)
[1] "class" "posterior" "x"
Это возвращает список с тремя переменными:
- класс: предсказанный класс
- апостериорная: апостериорная вероятность того, что наблюдение принадлежит каждому классу
- x: линейные дискриминанты
Мы можем быстро просмотреть каждый из этих результатов для первых шести наблюдений в нашем тестовом наборе данных:
#view predicted class for first six observations in test set
head(predicted$class)
[1] setosa setosa setosa setosa setosa setosa
Levels: setosa versicolor virginica
#view posterior probabilities for first six observations in test set
head(predicted$posterior)
setosa versicolor virginica
4 1 2.425563e-17 1.341984e-35
6 1 1.400976e-21 4.482684e-40
7 1 3.345770e-19 1.511748e-37
15 1 6.389105e-31 7.361660e-53
17 1 1.193282e-25 2.238696e-45
18 1 6.445594e-22 4.894053e-41
#view linear discriminants for first six observations in test set
head(predicted$x)
LD1 LD2
4 7.150360 -0.7177382
6 7.961538 1.4839408
7 7.504033 0.2731178
15 10.170378 1.9859027
17 8.885168 2.1026494
18 8.113443 0.7563902
Мы можем использовать следующий код, чтобы увидеть, для какого процента наблюдений модель LDA правильно предсказала виды:
#find accuracy of model
mean(predicted$class==test$Species)
[1] 1
Оказывается, модель правильно предсказала виды для 100% наблюдений в нашем тестовом наборе данных.
В реальном мире модель LDA редко будет правильно предсказывать результат каждого класса, но этот набор данных радужной оболочки просто построен таким образом, что алгоритмы машинного обучения, как правило, работают с ним очень хорошо.
Шаг 7: Визуализируйте результаты
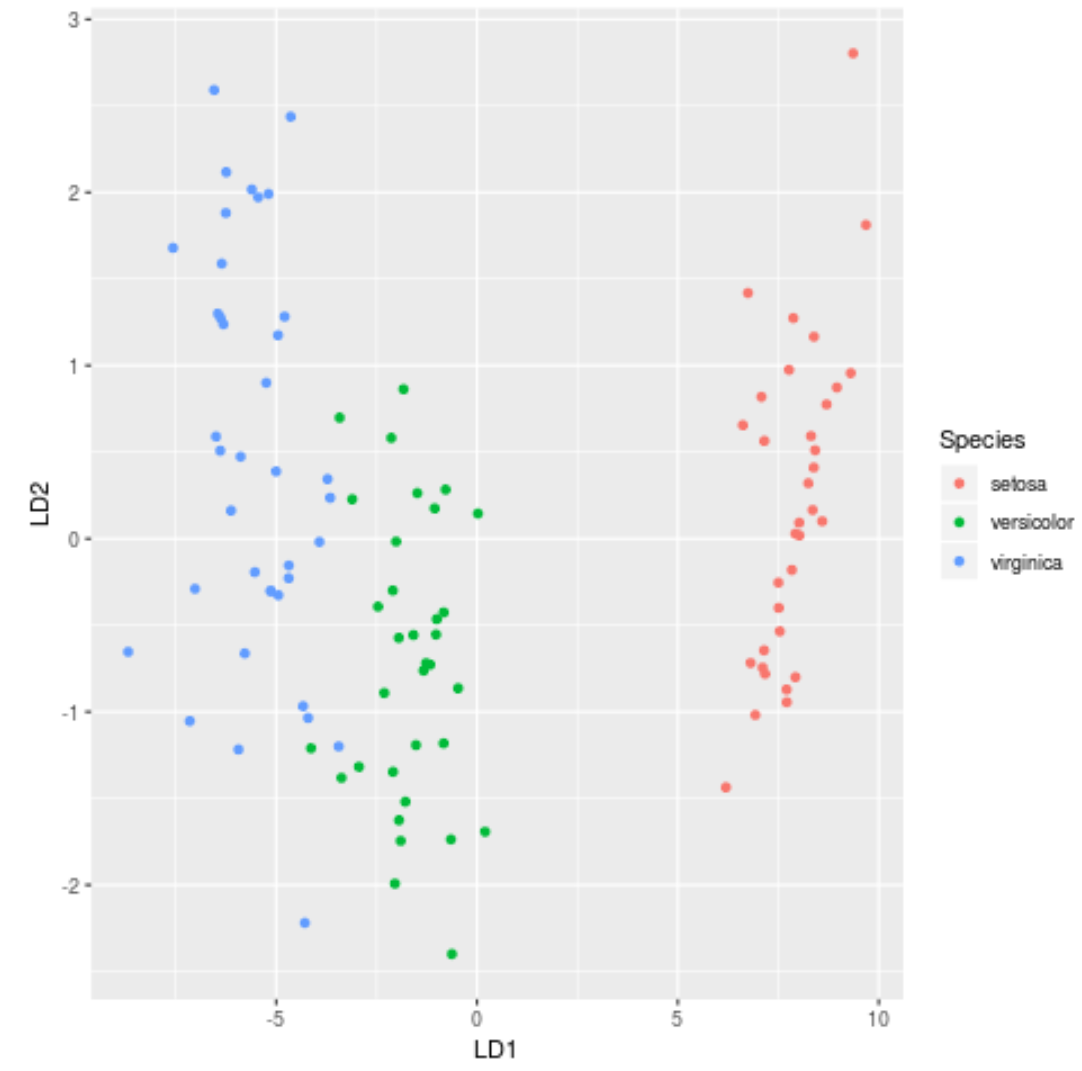
Наконец, мы можем создать график LDA, чтобы просмотреть линейные дискриминанты модели и визуализировать, насколько хорошо она разделила три разных вида в нашем наборе данных:
#define data to plot
lda_plot <- cbind(train, predict(model)$x)
#create plot
ggplot(lda_plot, aes (LD1, LD2)) +
geom_point( aes (color = Species))
Вы можете найти полный код R, использованный в этом руководстве , здесь .