Логарифмический ранговый тест является наиболее распространенным способом сравнения кривых выживаемости между двумя группами.
В этом тесте используются следующие гипотезы :
H 0 : Нет никакой разницы в выживаемости между двумя группами.
H A : Существует разница в выживаемости между двумя группами.
Если p-значение теста меньше некоторого уровня значимости (например, α = 0,05), то мы можем отклонить нулевую гипотезу и сделать вывод, что имеется достаточно доказательств, говорящих о разнице в выживаемости между двумя группами.
Чтобы выполнить тест логарифмического ранга в R, мы можем использовать функцию survdiff() из пакета выживания , которая использует следующий синтаксис:
survdiff(Surv(время, статус) ~ предикторы, данные)
Эта функция возвращает статистику теста хи-квадрат и соответствующее значение p.
В следующем примере показано, как использовать эту функцию для выполнения теста логарифмического ранга в R.
Пример: логарифмический ранговый тест в R
В этом примере мы будем использовать набор данных яичников из пакета выживания.Этот набор данных содержит следующую информацию о 26 пациентах:
- Продолжительность жизни (в месяцах) после постановки диагноза рака яичников
- Было ли время выживания подвергнуто цензуре
- Тип полученного лечения (rx = 1 или rx = 2)
Следующий код показывает, как просмотреть первые шесть строк этого набора данных:
library (survival)
#view first six rows of dataset
head(ovarian)
futime fustat age resid.ds rx ecog.ps
1 59 1 72.3315 2 1 1
2 115 1 74.4932 2 1 1
3 156 1 66.4658 2 1 2
4 421 0 53.3644 2 2 1
5 431 1 50.3397 2 1 1
6 448 0 56.4301 1 1 2
В следующем коде показано, как выполнить логарифмический ранговый тест, чтобы определить, есть ли разница в выживаемости между пациентами, получавшими разное лечение:
#perform log rank test
survdiff(Surv(futime, fustat) ~ rx, data=ovarian)
Call:
survdiff(formula = Surv(futime, fustat) ~ rx, data = ovarian)
N Observed Expected (O-E)^2/E (O-E)^2/V
rx=1 13 7 5.23 0.596 1.06
rx=2 13 5 6.77 0.461 1.06
Chisq= 1.1 on 1 degrees of freedom, p= 0.3
Статистика критерия хи-квадрат равна 1,1 с 1 степенью свободы, а соответствующее значение p равно 0,3.Поскольку это p-значение не меньше 0,05, мы не можем отвергнуть нулевую гипотезу.
Другими словами, у нас нет достаточных доказательств, чтобы сказать, что существует статистически значимая разница в выживаемости между двумя видами лечения.
Мы также можем построить кривые выживания для каждой группы, используя следующий синтаксис:
#plot survival curves for each treatment group
plot(survfit(Surv(futime, fustat) ~ rx, data = ovarian),
xlab = " Time",
ylab = " Overall survival probability ")
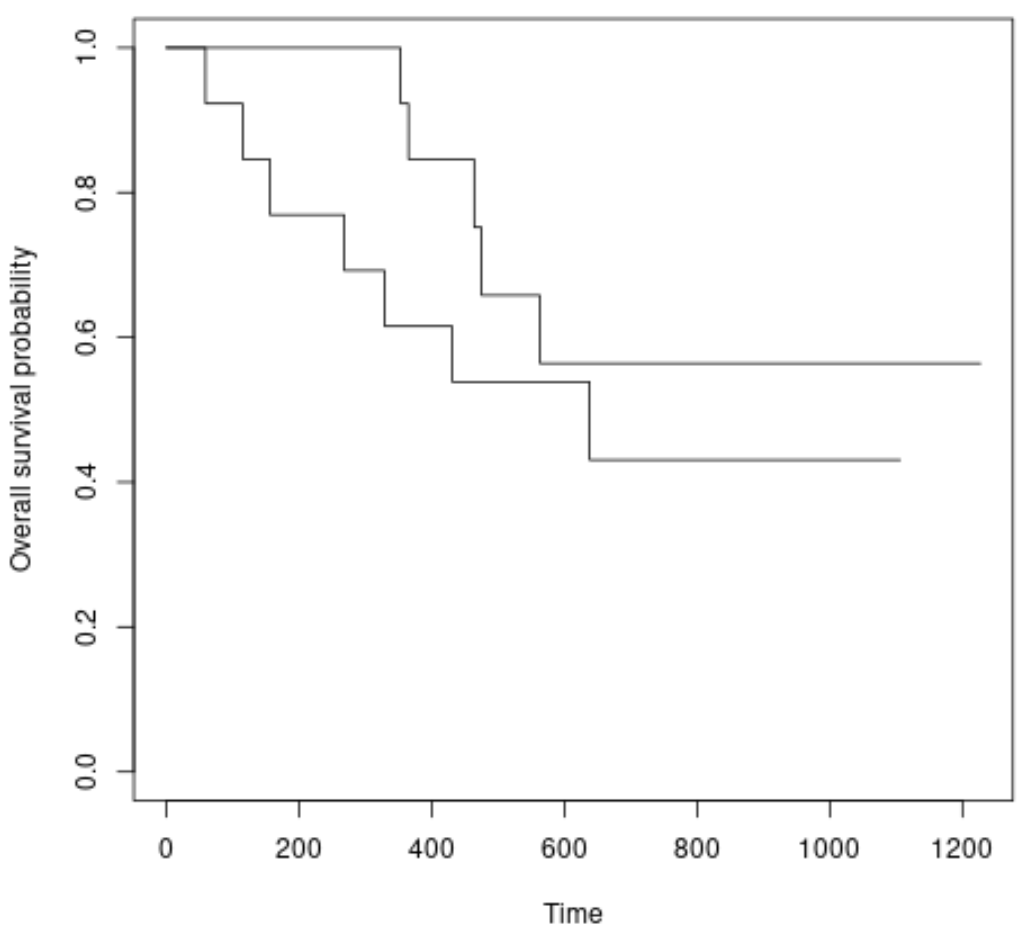
Мы видим, что кривые выживаемости немного отличаются, но логарифмический ранговый тест показал нам, что разница не является статистически значимой.