Однофакторный дисперсионный анализ используется для определения того, приводят ли различные уровни объясняющей переменной к статистически различным результатам в некоторой переменной отклика.
Например, нам может быть интересно понять, приводят ли три уровня образования (степень младшего специалиста, степень бакалавра, степень магистра) к статистически разным годовым доходам. В этом случае у нас есть одна объясняющая переменная и одна переменная отклика.
- Объясняющая переменная: уровень образования
- Переменная ответа: годовой доход
MANOVA — это расширение однофакторного дисперсионного анализа, в котором имеется более одной переменной отклика. Например, нам может быть интересно понять, приводит ли уровень образования к разным годовым доходам и разным суммам долга по студенческим кредитам. В этом случае у нас есть одна объясняющая переменная и две переменные отклика:
- Объясняющая переменная: уровень образования
- Переменные ответа: годовой доход, задолженность по студенческому кредиту.
Поскольку у нас есть более одной переменной отклика, в этом случае было бы уместно использовать MANOVA.
В этом руководстве мы объясним, как выполнить MANOVA в SPSS.
Пример: MANOVA в SPSS
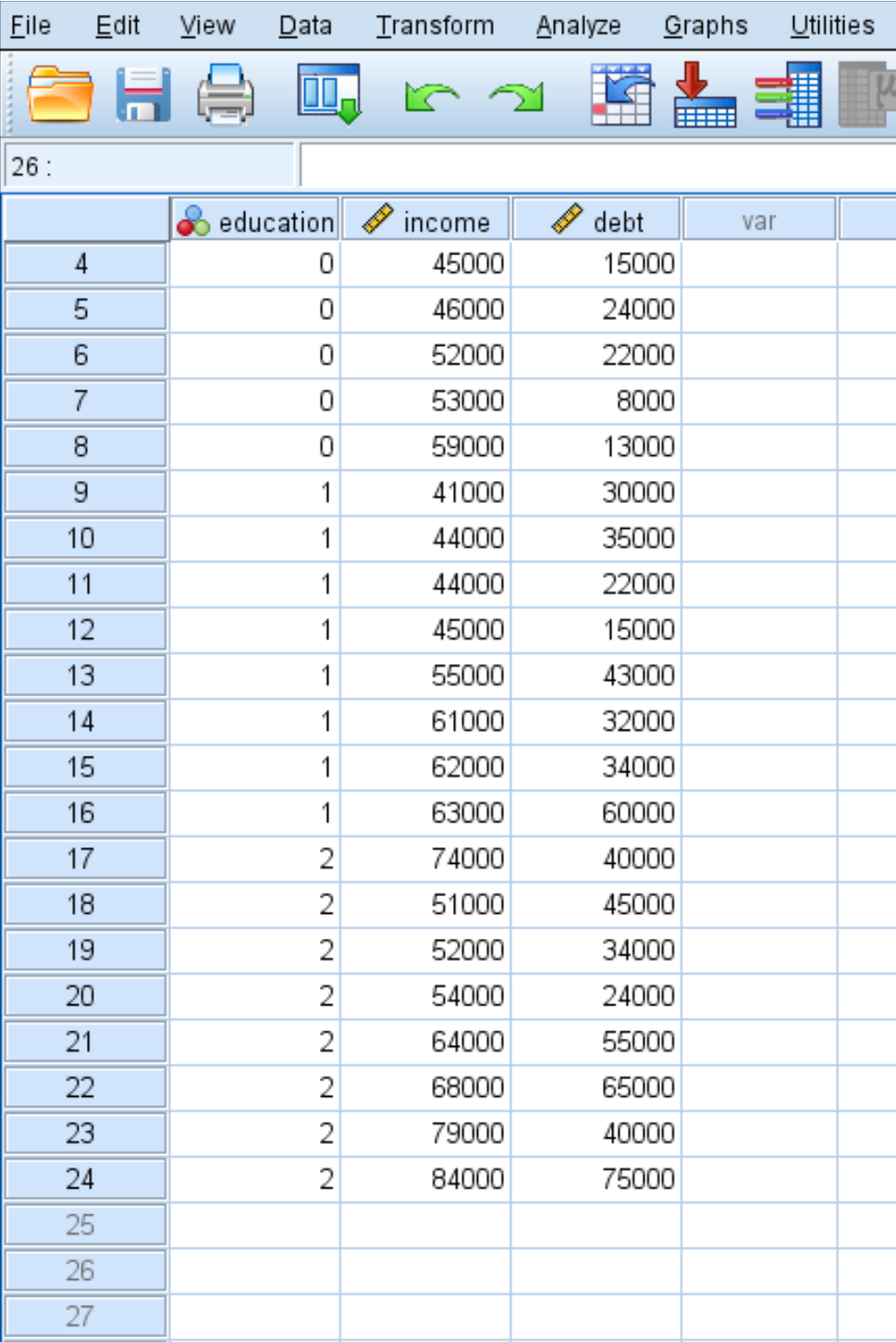
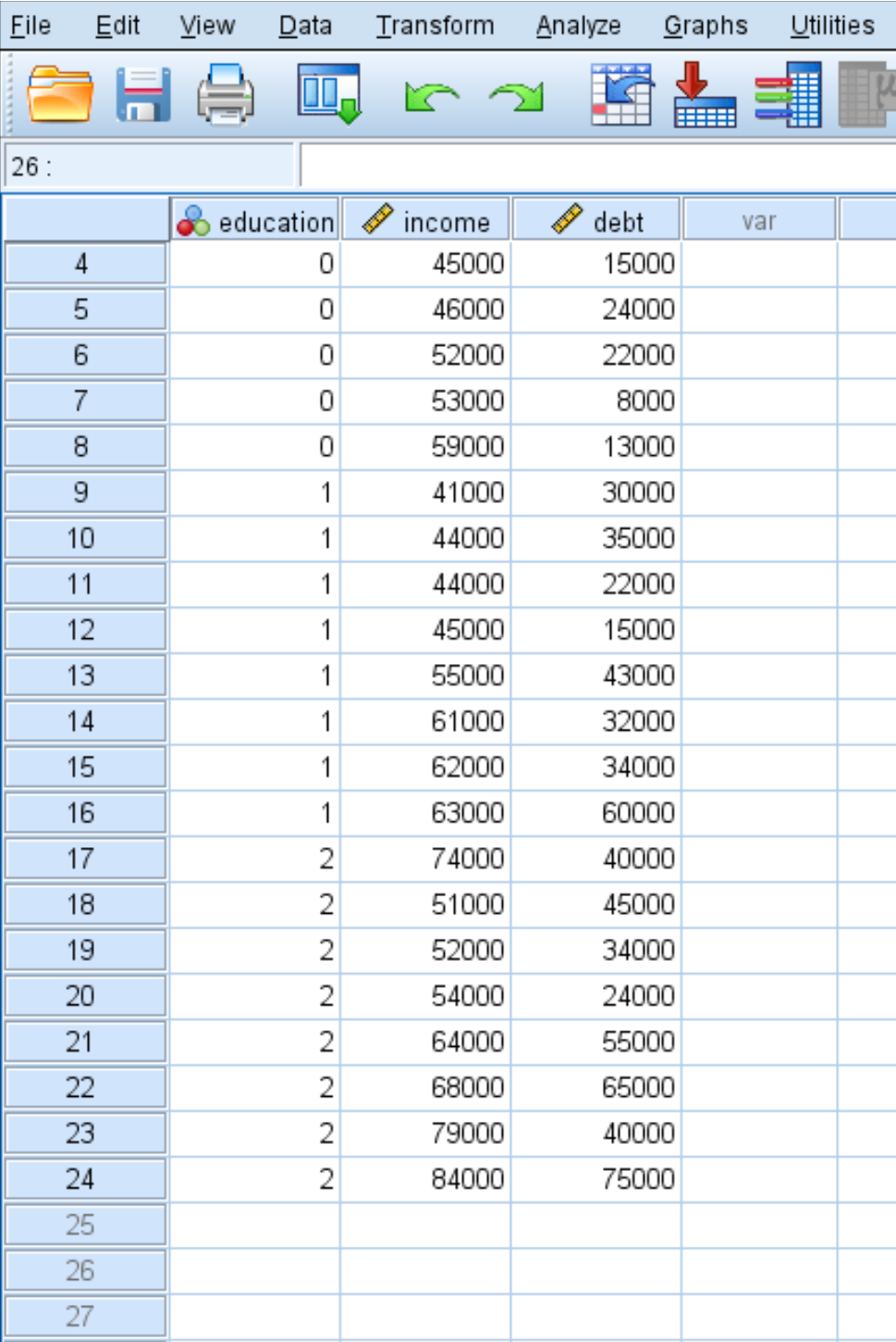
Чтобы проиллюстрировать, как выполнить MANOVA в SPSS, мы будем использовать следующий набор данных, который содержит следующие три переменные для 24 человек:
- educ: уровень образования (0 = Associate, 1 = Bachelor, 2 = Master)
- доход: годовой доход
- долг: общая задолженность по студенческому кредиту
Используйте следующие шаги для выполнения MANOVA в SPSS:
Шаг 1: Выполните MANOVA.
Перейдите на вкладку « Анализ », затем « Общая линейная модель », затем « Многомерная модель»:
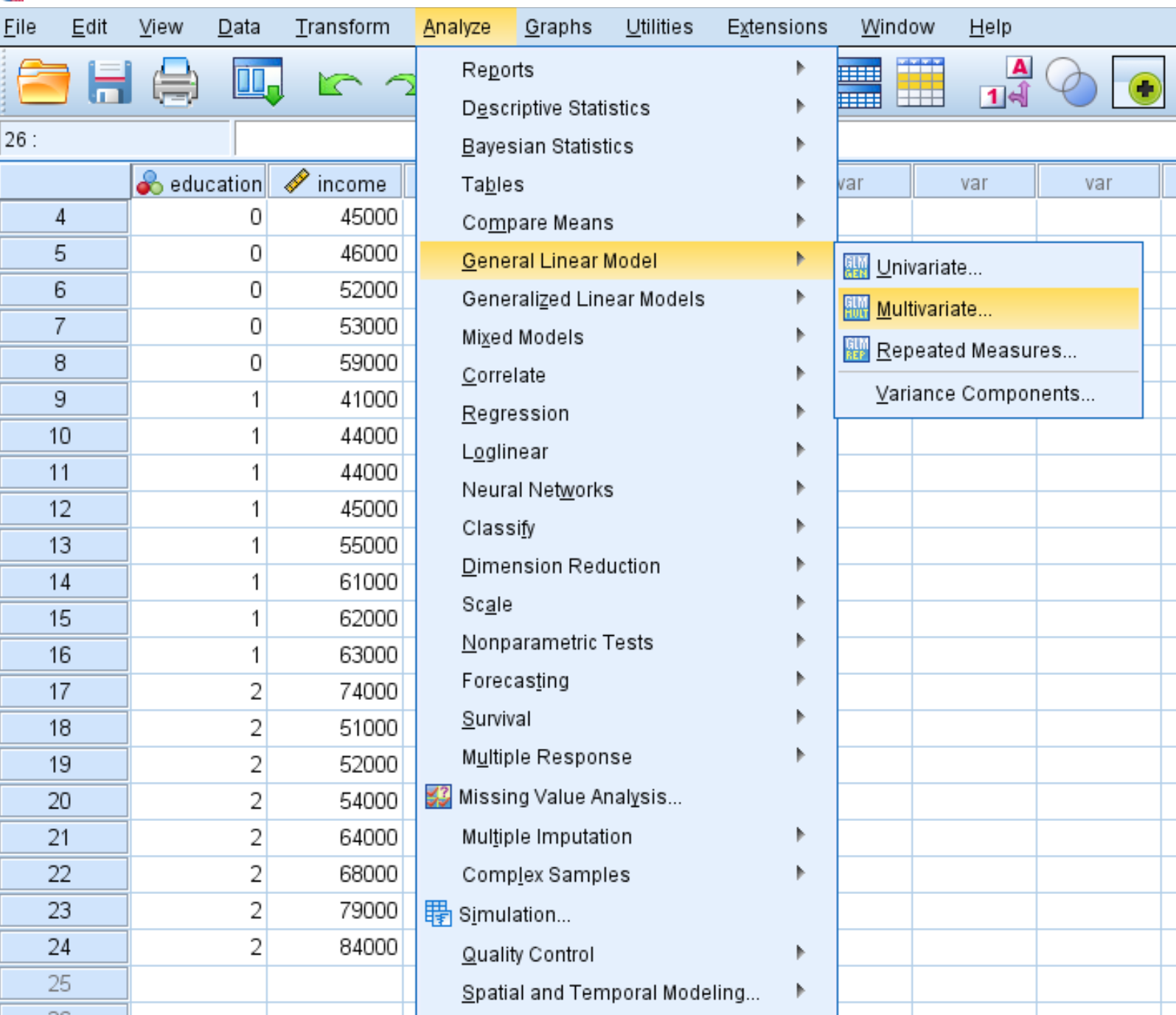
В появившемся новом окне перетащите переменные доход и долг в поле с надписью Зависимые переменные. Затем перетащите факторную переменную образования в поле Фиксированные факторы:
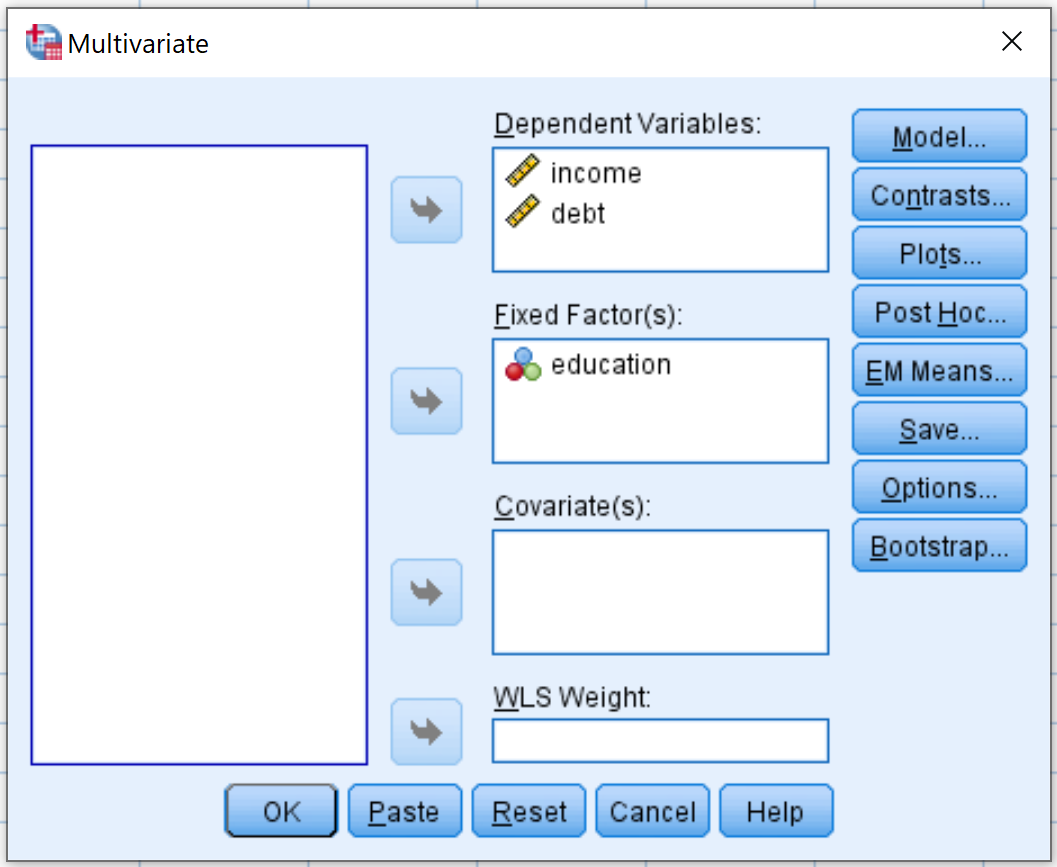
Далее нажмите кнопку Post Hoc.Перетащите фактор образования в поле с надписью Апостериорные тесты для.Затем установите флажок рядом с Tukey.Затем нажмите «Продолжить» .
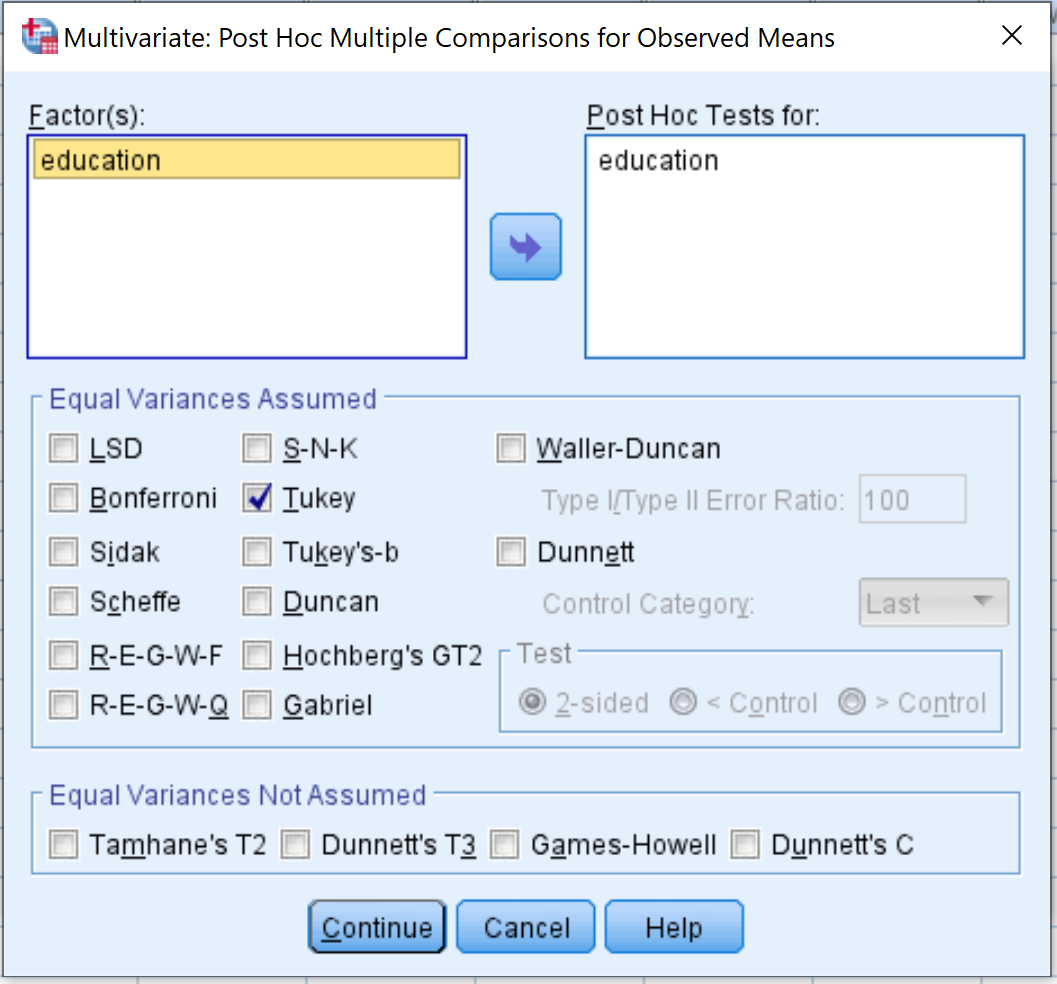
Наконец, нажмите ОК .
Шаг 2: Интерпретируйте результаты.
Как только вы нажмете OK , появятся результаты MANOVA. Вот как интерпретировать вывод:
Многовариантные тесты
Эта таблица показывает, приводит ли уровень образования к статистически значимым различиям в годовом доходе и общем студенческом долге. Мы посмотрим на числа в строке под названием «Лямбда Уилкса» :
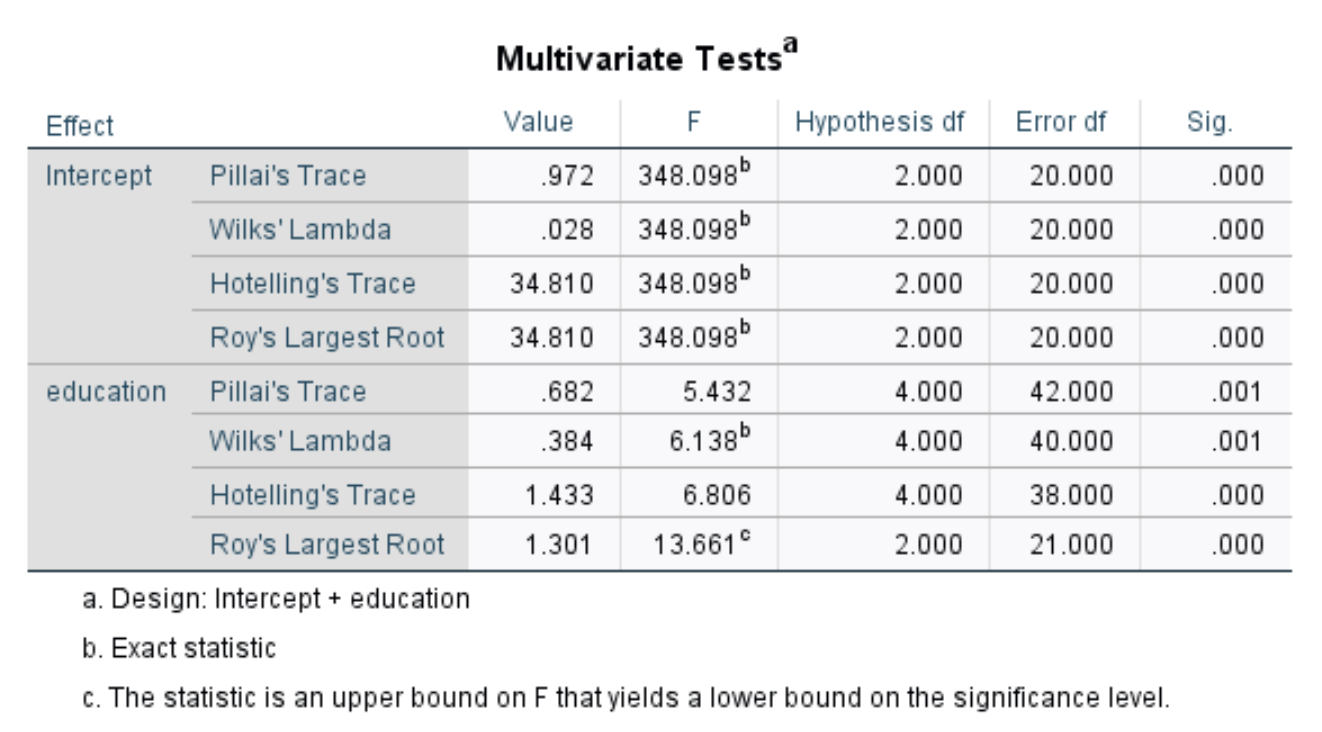
Общая статистика F составляет 6,138 , а соответствующее значение p равно 0,001.Поскольку это значение меньше 0,05, это указывает на то, что уровень образования оказывает значительное влияние на годовой доход и общий студенческий долг.
Тесты межсубъектных эффектов
В этой таблице показаны отдельные p-значения как для дохода , так и для долга :
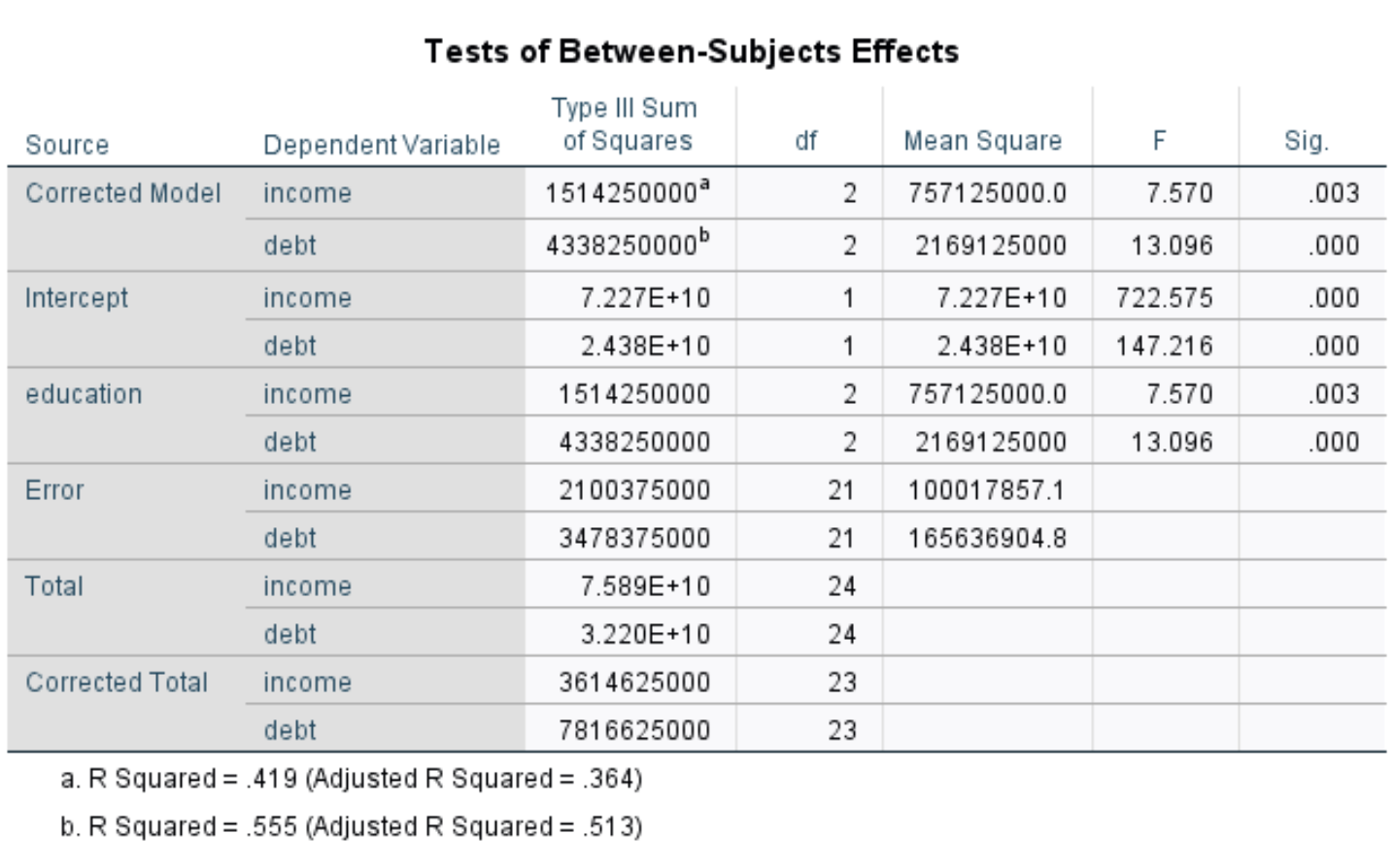
Р-значение дохода равно 0,003 , а р-значение долга равно 0,000.Поскольку оба этих значения меньше 0,05, это означает, что уровень образования оказывает статистически значимое влияние как на доход, так и на долг.
Апостериорные тесты
В этой таблице показаны апостериорные сравнения Тьюки для каждого уровня образования.
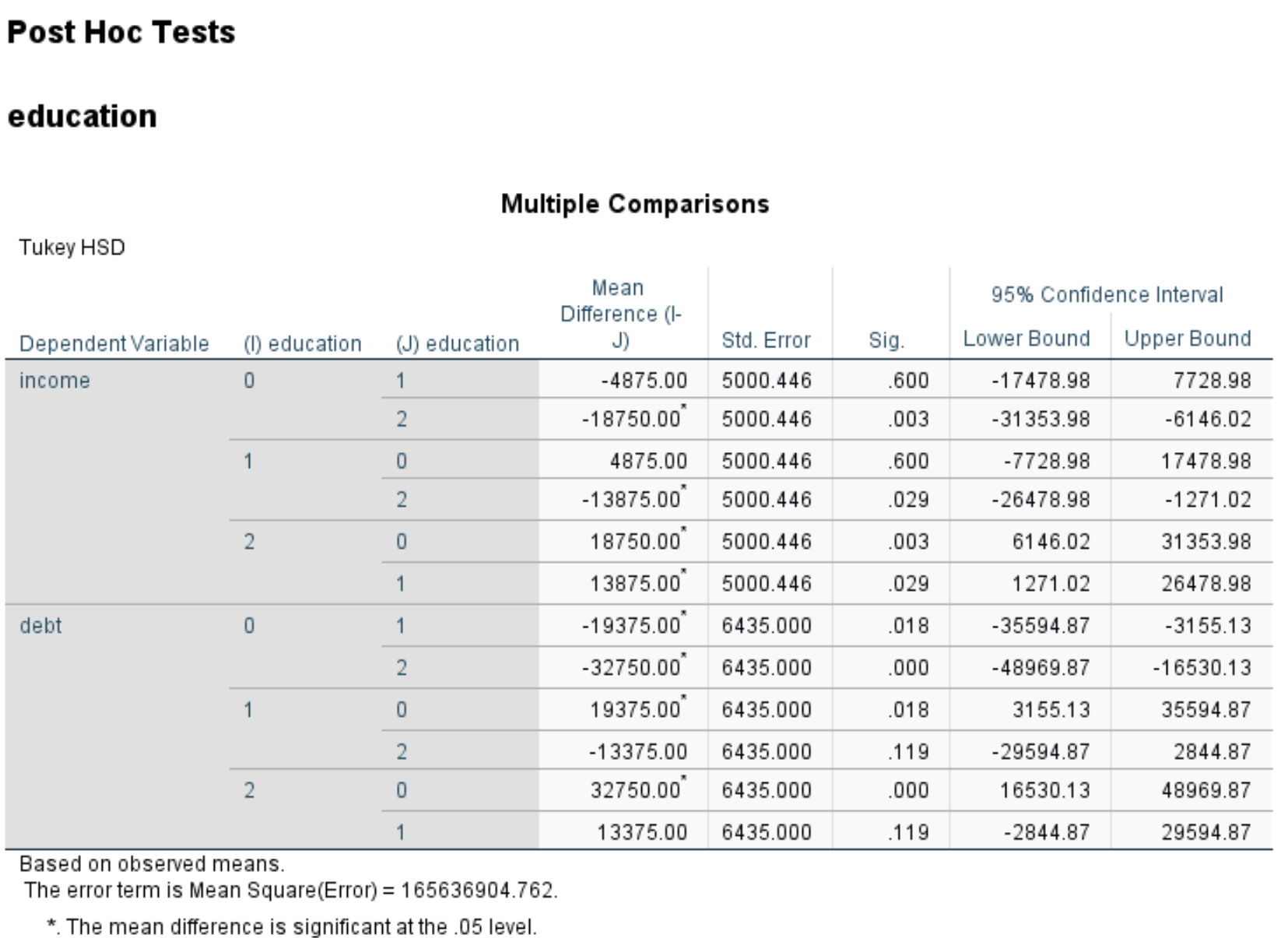
Из таблицы мы можем наблюдать следующее:
- Сумма дохода лиц со степенью младшего специалиста (образование=0) значительно отличается от суммы дохода лиц со степенью магистра (образование=1) | р-значение = 0,003 .
- Сумма дохода лиц со степенью бакалавра (образование=1) существенно отличается от суммы дохода лиц со степенью магистра (образование=2) | р-значение = 0,029 .
- Сумма дохода лиц со степенью младшего специалиста (образование=0) значительно отличается от суммы дохода лиц со степенью бакалавра (образование=1) | р-значение = 0,018 .
- Сумма дохода лиц со степенью младшего специалиста (образование=0) значительно отличается от суммы дохода лиц со степенью магистра (образование=2) | p-значение = 0,000 .
Дополнительная литература: различия между ANOVA, ANCOVA, MANOVA и MANCOVA