Часто в статистике мы используем доверительные интервалы для оценки значения параметра совокупности с определенным уровнем достоверности.
Каждый доверительный интервал принимает следующий вид:
Доверительный интервал = [нижняя граница, верхняя граница]
Погрешность равна половине ширины всего доверительного интервала.
Например, предположим, что у нас есть следующий доверительный интервал для среднего значения генеральной совокупности:
95% доверительный интервал = [12,5, 18,5]
Ширина доверительного интервала составляет 18,5 – 12,5 = 6. Допустимая погрешность равна половине ширины, которая будет равна 6/2 = 3 .
В следующих примерах показано, как рассчитать доверительный интервал вместе с погрешностью для нескольких различных сценариев.
Пример 1: Доверительный интервал и допустимая погрешность для среднего значения генеральной совокупности
Мы используем следующую формулу для расчета доверительного интервала для среднего значения генеральной совокупности:
Доверительный интервал = x +/- z*(s/ √n )
куда:
- x : выборочное среднее
- z: z-критическое значение
- s: стандартное отклонение выборки
- n: размер выборки
Пример: Предположим, мы собираем случайную выборку дельфинов со следующей информацией:
- Размер выборки n = 40
- Средний вес выборки x = 300
- Стандартное отклонение выборки s = 18,5
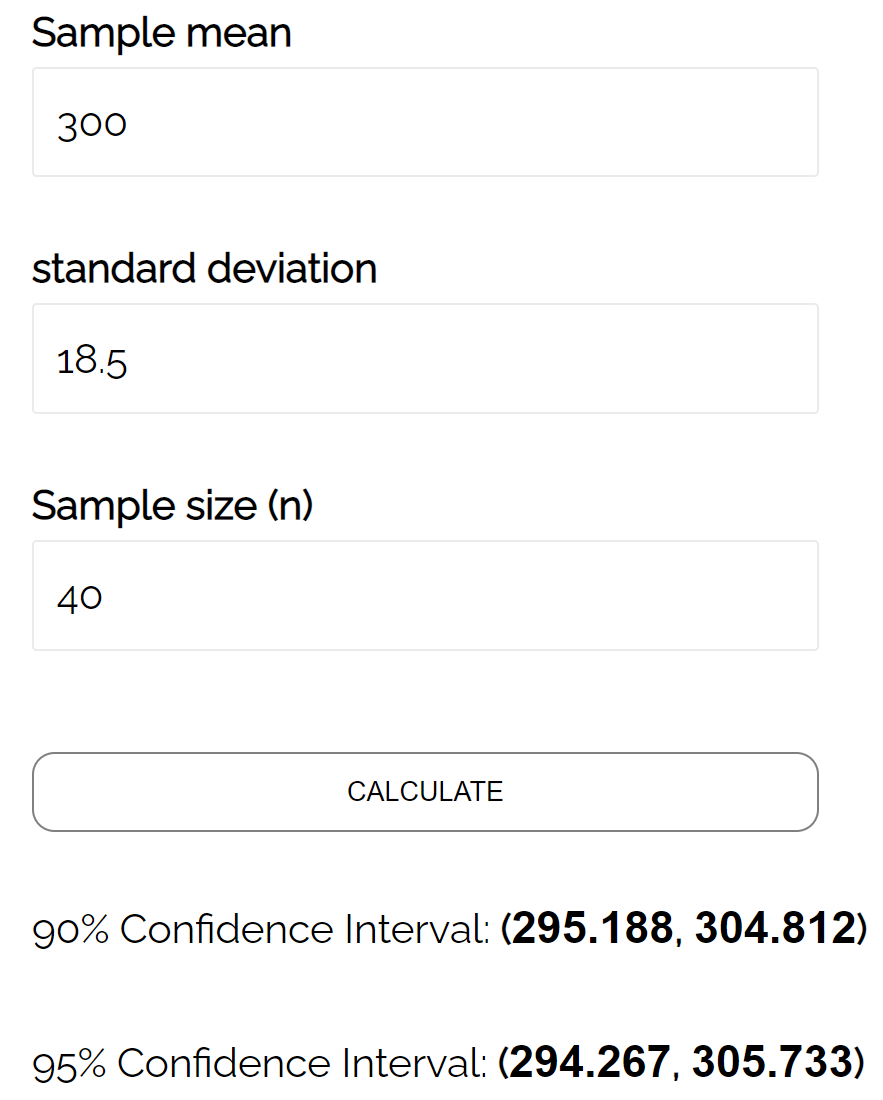
Мы можем подставить эти числа в калькулятор доверительного интервала , чтобы найти 95% доверительный интервал:
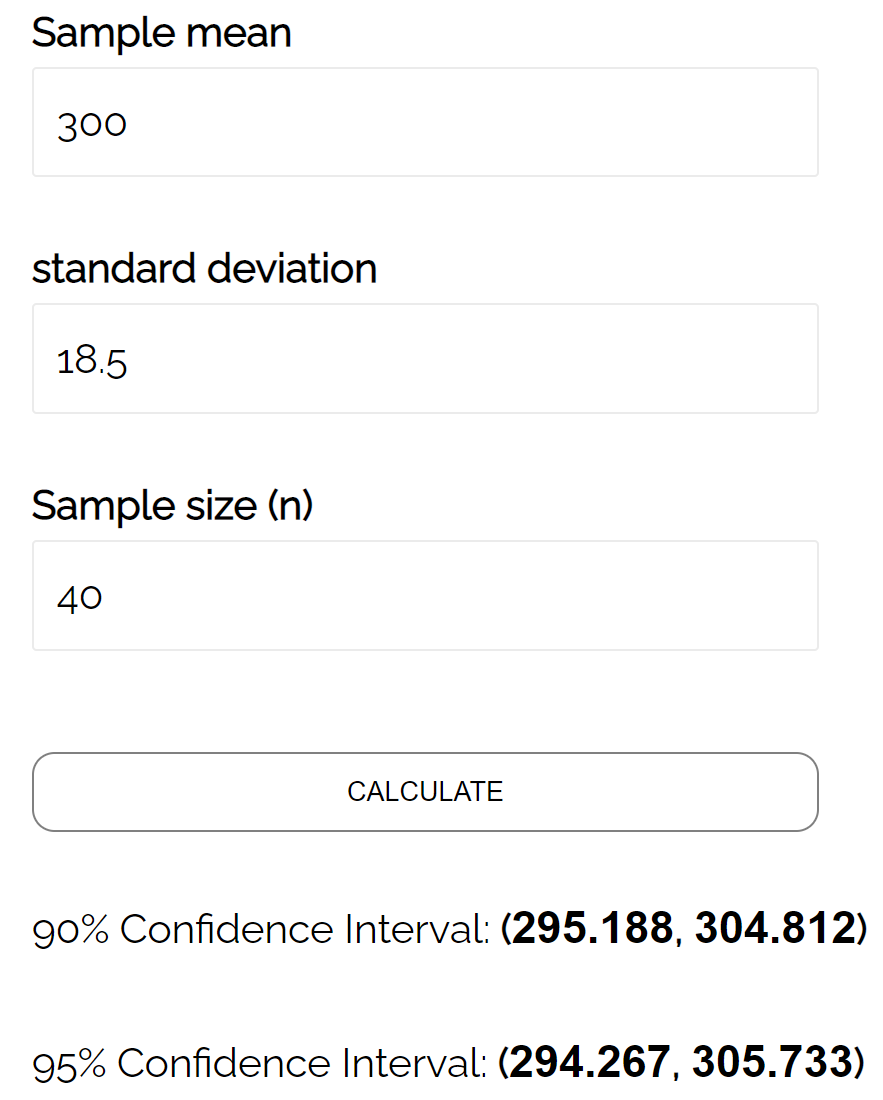
95% доверительный интервал для истинного среднего веса популяции черепах составляет [294,267, 305,733] .
Погрешность будет равна половине ширины доверительного интервала, который равен:
Погрешность: (305,733 – 294,267) / 2 = 5,733 .
Пример 2: Доверительный интервал и допустимая погрешность для доли населения
Мы используем следующую формулу для расчета доверительного интервала для доли населения:
Доверительный интервал = p +/- z * (√ p (1-p) / n )
куда:
- p: доля выборки
- z: выбранное значение z
- n: размер выборки
Пример: Предположим, мы хотим оценить долю жителей округа, поддерживающих определенный закон. Мы выбираем случайную выборку из 100 жителей и спрашиваем их об их отношении к закону. Вот результаты:
- Размер выборки n = 100
- Доля в пользу закона p = 0,56
Мы можем подставить эти числа в доверительный интервал для калькулятора пропорций , чтобы найти 95% доверительный интервал:

95% доверительный интервал для истинной доли населения составляет [0,4627, 0,6573] .
Погрешность будет равна половине ширины доверительного интервала, который равен:
Погрешность: (0,6573 – 0,4627) / 2 = 0,0973 .
Дополнительные ресурсы
Погрешность и стандартная ошибка: в чем разница?
Как найти погрешность в Excel
Как найти погрешность на калькуляторе TI-84