Вы можете найти медианное значение таблицы частот, выполнив следующие действия:
Шаг 1: Расположите все отдельные значения от наименьшего к наибольшему.
Шаг 2: Определите значение прямо в середине упорядоченного списка.
- Если имеется нечетное количество значений, медианой является значение, находящееся непосредственно посередине.
- Если имеется четное количество значений, медиана является средним значением двух средних значений.
В следующих примерах показано, как на практике найти медианное значение таблицы частот.
Пример 1: Медиана из таблицы частот (нечетное количество значений)
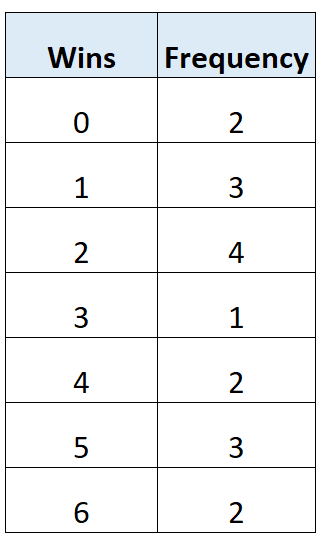
В следующей таблице частоты показано общее количество побед 17 футбольных команд в определенной лиге:
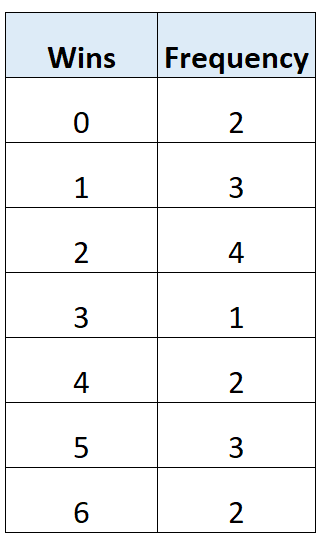
Мы можем использовать следующие шаги, чтобы найти медианное значение в этой таблице частот:
Шаг 1: Расположите все отдельные значения от наименьшего к наибольшему.
Значения: 0, 0, 1, 1, 1, 2, 2, 2, 2, 3, 4, 4, 5, 5, 5, 6, 6
Шаг 2: Определите значение прямо в середине упорядоченного списка.
Значения: 0, 0, 1, 1, 1, 2, 2, 2, 2 , 3, 4, 4, 5, 5, 5, 6, 6
Среднее значение равно 2 .
Пример 2: Медиана из таблицы частот (четное число значений)
В следующей таблице частот показан размер домохозяйства 20 различных домохозяйств в определенном районе:
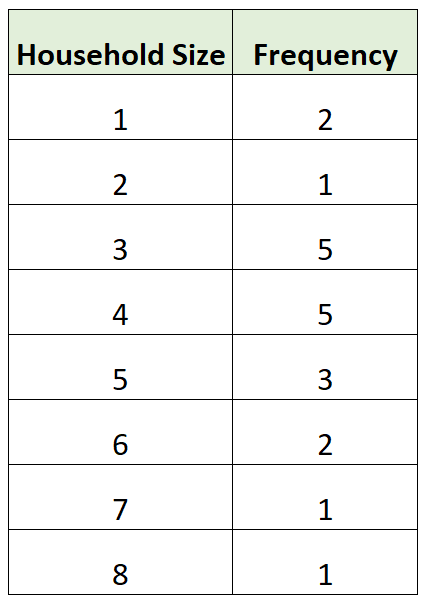
Мы можем использовать следующие шаги, чтобы найти медианное значение в этой таблице частот:
Шаг 1: Расположите все отдельные значения от наименьшего к наибольшему.
Значения: 1, 1, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 5, 5, 5, 6, 6, 7, 8
Шаг 2: Определите значение прямо в середине упорядоченного списка.
Значения: 1, 1, 2, 3, 3, 3, 3, 3, 4, 4 , 4 , 4, 4, 5, 5, 5, 6, 6, 7, 8
Прямо посередине расположены два значения: 4 и 4.
Таким образом, медианное значение является средним из этих двух значений: (4 + 4)/2 = 4 .
Дополнительные ресурсы
Как рассчитать среднее значение из таблицы частот
Как рассчитать моду из таблицы частот
Как оценить среднее значение и медиану гистограмм
Когда использовать среднее значение против медианы