Гистограмма — это диаграмма, которая помогает нам визуализировать распределение значений в наборе данных.
По оси X гистограммы отображаются интервалы значений данных, а по оси Y указано, сколько наблюдений в наборе данных приходится на каждый интервал.
Хотя гистограммы полезны для визуализации распределений, не всегда очевидно, что представляют собой средние и медианные значения, просто взглянув на гистограммы.
И хотя невозможно найти точное среднее и срединное значения распределения, просто взглянув на гистограмму, можно оценить оба значения. В этом руководстве объясняется, как это сделать.
Как оценить среднее значение гистограммы
Мы можем использовать следующую формулу, чтобы найти наилучшую оценку среднего значения любой гистограммы:
Наилучшая оценка среднего: Σm i n i / N
куда:
- m i : середина i -го бина
- n i : частота i -го бина
- N: общий размер выборки
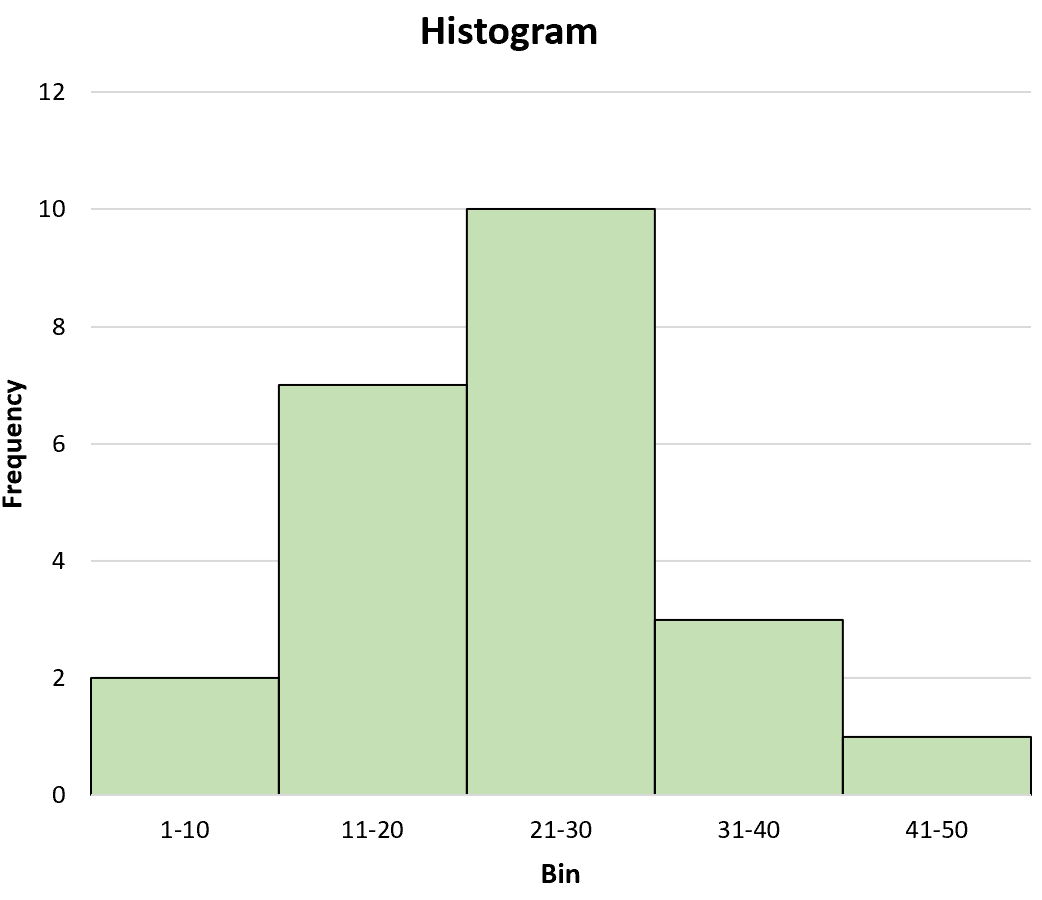
Например, рассмотрим следующую гистограмму:

Наилучшей оценкой среднего значения будет:
Среднее значение = (5,5*2 + 15,5*7 + 25,5*10 + 35,5*3 + 45,5*1) / 23 = 22,89 .
Глядя на гистограмму, это кажется разумной оценкой среднего значения.
Как оценить медиану гистограммы
Мы можем использовать следующую формулу, чтобы найти наилучшую оценку медианы любой гистограммы:
Наилучшая оценка медианы: L + ((n/2 – F)/f) * w
куда:
- L: Нижний предел средней группы
- n: общее количество наблюдений
- F: кумулятивная частота до средней группы
- f: частота срединной группы
- w: ширина срединной группы
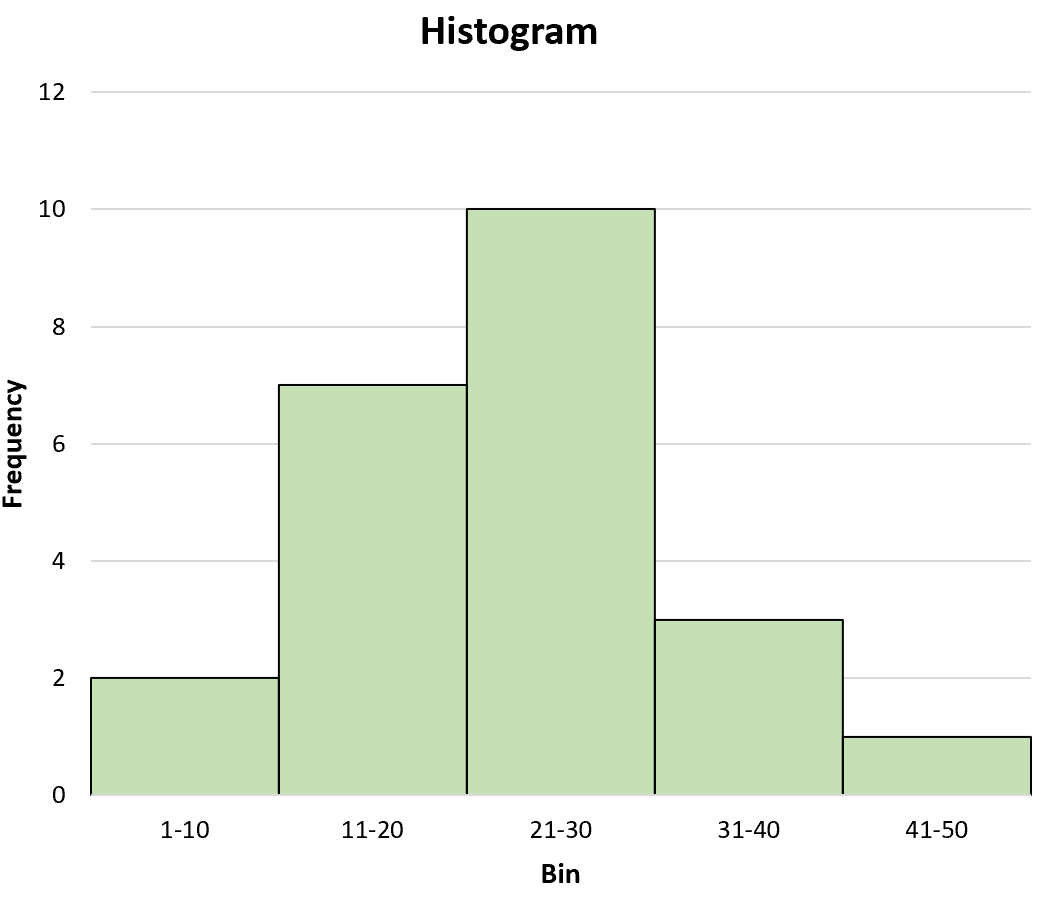
Еще раз рассмотрим следующую гистограмму:

Наилучшей оценкой медианы будет:
Медиана = 21 + ((25/2 – 9)/10) * 9 = 24,15 .
Глядя на гистограмму, это также кажется разумной оценкой медианы.
Связанный: Как оценить стандартное отклонение любой гистограммы
Дополнительные ресурсы
Как найти среднее значение, медиану и моду в диаграммах «стебель-и-листья»
Как рассчитать среднее значение из таблиц частот
Когда использовать среднее значение против медианы