Многие статистические тесты предполагают, что значения в наборе данных имеют нормальное распределение .
Один из самых простых способов проверить это предположение — выполнить тест Харке-Бера , который представляет собой тест согласия, который определяет, имеют ли выборочные данные асимметрию и эксцесс, соответствующие нормальному распределению.
В этом тесте используются следующие гипотезы:
H 0 : Данные нормально распределены.
H A : Данные не распределены нормально.
Тестовая статистика JB определяется как:
JB = (n/6) * (S 2 + (C 2 /4))
куда:
- n: количество наблюдений в выборке
- S: асимметрия выборки
- C: образец эксцесса
При нулевой гипотезе нормальности JB ~ X 2 (2).
Если значение p , соответствующее тестовой статистике, меньше некоторого уровня значимости (например, α = 0,05), то мы можем отклонить нулевую гипотезу и сделать вывод, что данные не распределены нормально.
В этом руководстве представлен пошаговый пример того, как выполнить тест Харке-Бера для заданного набора данных в Excel.
Шаг 1: Создайте данные
Во-первых, давайте создадим поддельный набор данных с 15 значениями:
Шаг 2: Рассчитайте тестовую статистику
Затем рассчитайте статистику теста JB. В столбце E показаны используемые формулы:
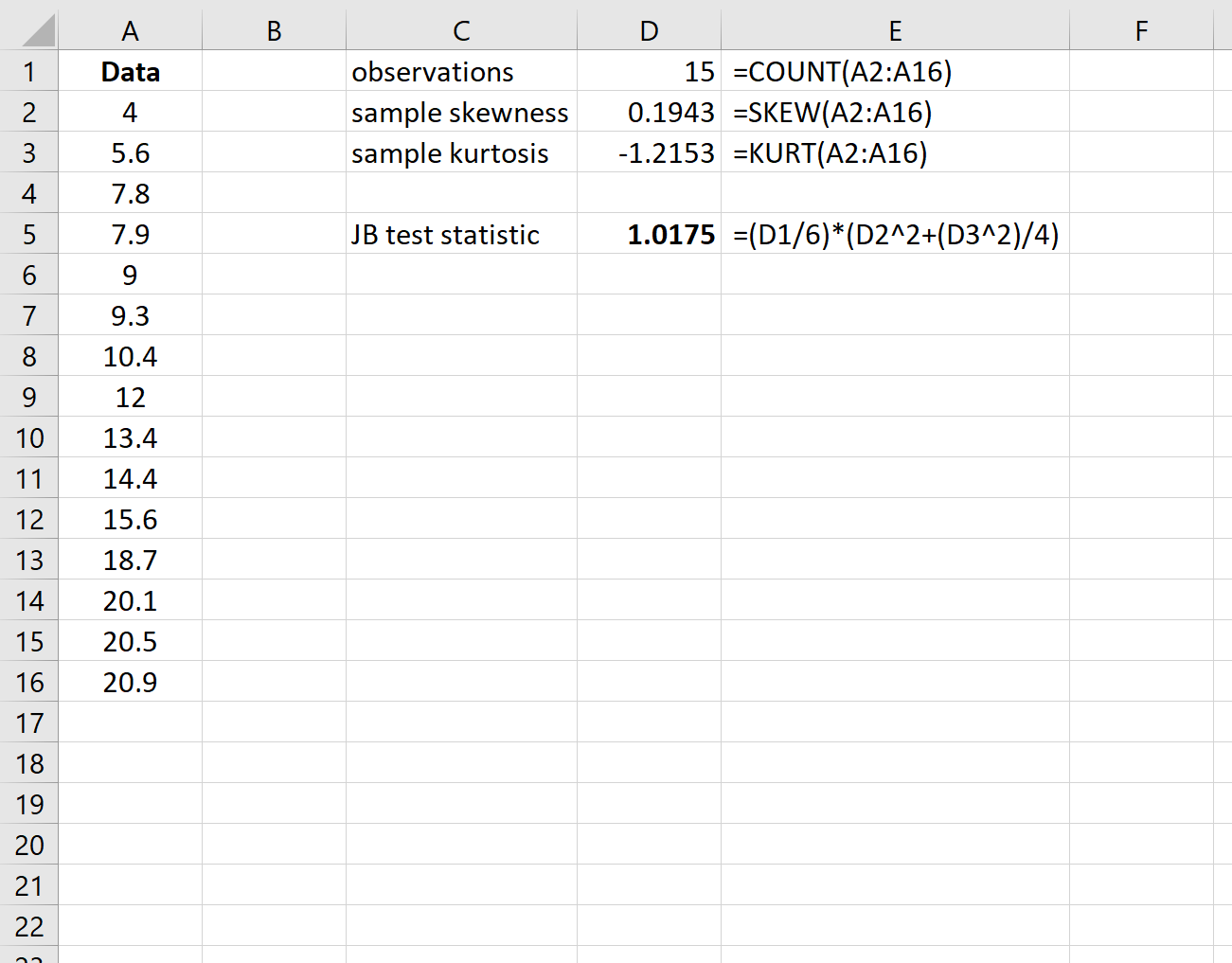
Тестовая статистика оказывается 1,0175 .
Шаг 3: Рассчитайте P-значение
При нулевой гипотезе нормальности тестовая статистика JB следует распределению хи-квадрат с 2 степенями свободы.
Итак, чтобы найти p-значение для теста, мы будем использовать следующую функцию в Excel: =CHISQ.DIST.RT(статистика теста JB, 2)
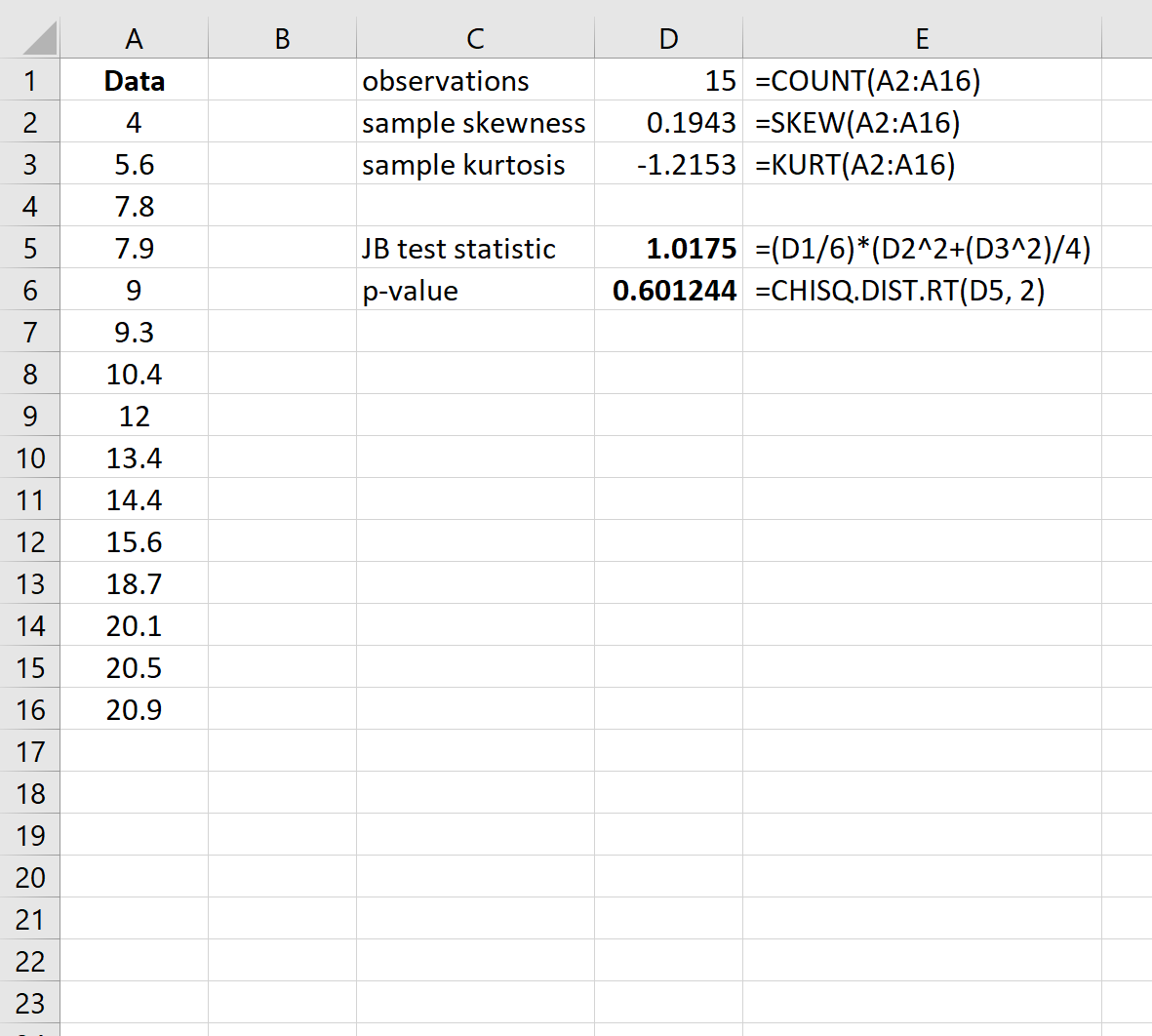
Значение p теста составляет 0,601244.Поскольку это p-значение не меньше 0,05, мы не можем отвергнуть нулевую гипотезу. У нас нет достаточных доказательств того, что набор данных не имеет нормального распределения.
Другими словами, мы можем предположить, что данные распределены нормально.
Дополнительные ресурсы
Как создать график QQ в Excel
Как выполнить критерий согласия хи-квадрат в Excel